Druckversion vom 27.07.2024 10:34 Uhr
Startseite Qualifikationsphase Analysis LK: Vertiefung Differentialrechnung
LK: Vertiefungen zur Analysis
| Zusammengesetzte Funktionen
In diesem Kapitel wird geklärt, was unter der Zusammensetzung von Funktionen verstanden wird. Dabei liegt der Schwerpunkt auf dem Verkettungsbegriff. Gebrochen-rationale Funktionen werden als Zusatzstoff angeboten. |
 |
| Vertiefungen zur Produktregel In diesem Kapitel werden ein algebraischer und ein geometrisch gestützter Beweis der Produktregel geführt. Zusätzlich werden zwei wichtige Problemlösemethoden thematisiert, nämlich das "Induktive Probieren" und das "Rückwärtsrechnen". |
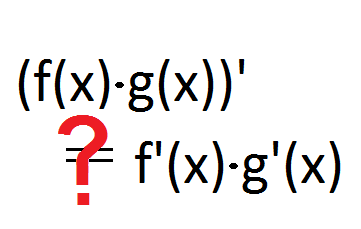 |
| Vertiefungen zur Kettenregel
Da in Sachzusammenhängen meist verkette Funktionen vorkommen, ist eine Behandlung dieses Funktionentyps und der entsprechenden Ableitungsregel unerlässlich. Um die sog. Kettenregel anwenden zu können, ist ein sicheres Erkennen der Verkettungsstruktur erforderlich. Die Herleitung der Kettenregel wird mithilfe bekannter Problemlösetrategien durchgeführt: Induktives Vermuten, Anwenden der Ableitungsdefinition, Rückwärtsrechnen. Dieser Teil dient daher nicht nur der Herleitung der Kettenregel, sondern auch der Festigung von Problemlösemethoden. |
 |
| Quotientenregel
Thema ist die Ableitung des Quotienten zweier Funktionen. Dazu wird der Quotient zweier Funktionen auf zwei verschiedene Arten in ein Produkt verwandelt. Mithilfe der Produktregel bzw. Kettenregel wird dann die Quotientenregel hergeleitet. Ein weiterer Zugang stützt sich auf die "induktive Methode", wie sie schon bei der Herleitung der Produktregel zum Einsatz kam. |
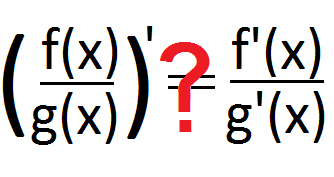 |
| Gebrochen rationale Funktionen
In diesem Kapitel werden gebrochen rationale Funktionen ausführlich untersucht. Die beiden Erforschen-Teile bauen aufeinander auf. Sie sind daher keine unabhängigen methodischen Zugänge in das Thema. Ehe Sie sich diesem Kapitel zuwenden, sollten Sie das Kapitel "Quotientenregel" bearbeiten.
|
|
| Ableitung von Funktionen mit rationalen Exponenten
Mithilfe der Kettenregel wird in diesem Kapitel die Ableitung von `f(x)=x^(n/m)` hergeleitet. |
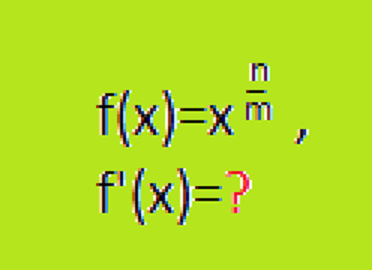 |
| Ableitung von Winkelfunktionen (optional)
Das Hauptziel dieses Kapitels, nämlich die Ableitungen von sinus und cosinus zu bestimmen, soll über verschiedene Problemlösemethoden erreicht werden:
Neben den Ableitungen von tangens und den arcus-Funktionen werden einige Modellierungsaufgaben behandelt. |
 |
| Logarithmusfunktionen
Inhalte dieses Kapitels: Logaritmus-Begriff, Rechnen mit Logarithmen, Logarithmus-Funktionen und deren Ableitungen sowie Anwendungen mit Logarithmen. Das Bild rechts zeigt einen Tiefdruckwirbel in Form einer logarithmischen Spirale. |
 |
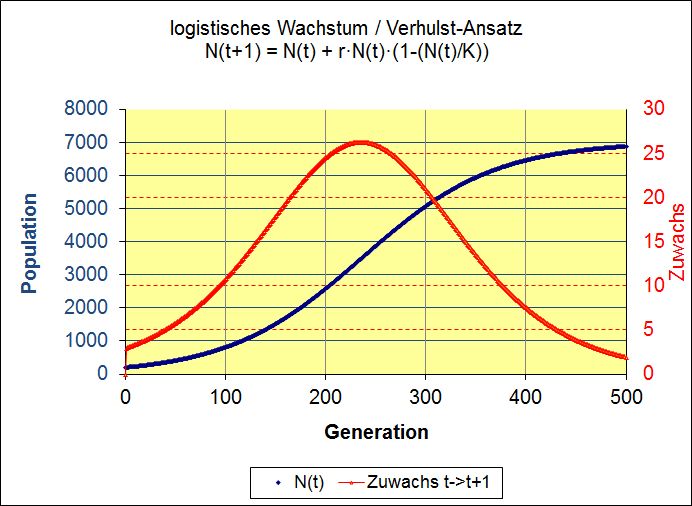
| Wachstumsprozesse
J.W.v.Goethe schreibt in seinem Sonett 'Wachstum': ... Nun kann den schönen Wachstum nichts beschränken; ...
Die Modelle der Mathematik untersuchen eher das Gegenteil: Beschränktes Wachstum und logistisches Wachstum! (und noch ein wenig mehr)
|
 |
| Weitere Anwendungen
Hier werden Probleme aus unterschiedlichen Anwendungsbereichen wie z.B. Verkehrswesen, Klimaforschung, Optik usw. behandelt. Die Lösung der Probleme, bei denen gebrochenrationale Funktionen auftreten, ist in den meisten Fällen auch ohne vorherige Bearbeitung des entsprechenden Teils im Kapitel "Zusammengesetzte Funktionen" möglich. |
 |
| Stetigkeit und Differenzierbarbeit (optional)
In diesem Unterrichtswerk werden an verschiedenen Stellen Funktionen zur Beschreibung von Wachstumsprozessen, Trassierungen, Flugbahnen usw. herangezogen. Dabei ist es oft wichtig, dass die Graphen solcher Funktionen keine Sprünge oder Knicke aufweisen. Hinter diesen Bezeichnungen stehen die mathematischen Begriffe Stetigkeit und Differenzierbarkeit. Diese mathematischen Begriffe werden hier ausführlich untersucht. Dabei stößt man auch auf Merkwürdigkeiten und exotische Funktionen. |
 |
| Zusammenfassung Ableitungsregeln
Hier finden Sie eine Zusammenfassung aller bisher behandelten Ableitungsregeln sowie die Ableitungen einiger spezieller Funktionen. |
 |



