Druckversion vom 27.07.2024 10:13 Uhr
Startseite Qualifikationsphase Analysis Ganzrationale Funktionen
Ganzrationale Funktionen
Im Zentrum dieses Kapitels steht die schon aus der Einführungsphase bekannte Klasse der Ganzrationalen Funktionen.
Hilfreich zur Bearbeitung der folgenden Kapitel ist, wenn Sie lineare Gleichungssysteme lösen können.
Vor der Darstellung der Kapitelinhalte geben wir zur Erinnerung die Definition an.
|
Eine reelle Funktion `f` heißt Polynom (oder ganzrationale Funktion) mit dem Grad `n (n epsilon NN)`, wenn `f(x) = a_n*x^n + a_(n - 1)*x^(n - 1) + a_(n - 2)*x^(n - 2) + ... + a_1*x^1 + a_0 ` mit `a_n != 0`
`f(x) = sum_(i=0)^n a_i*x^i`
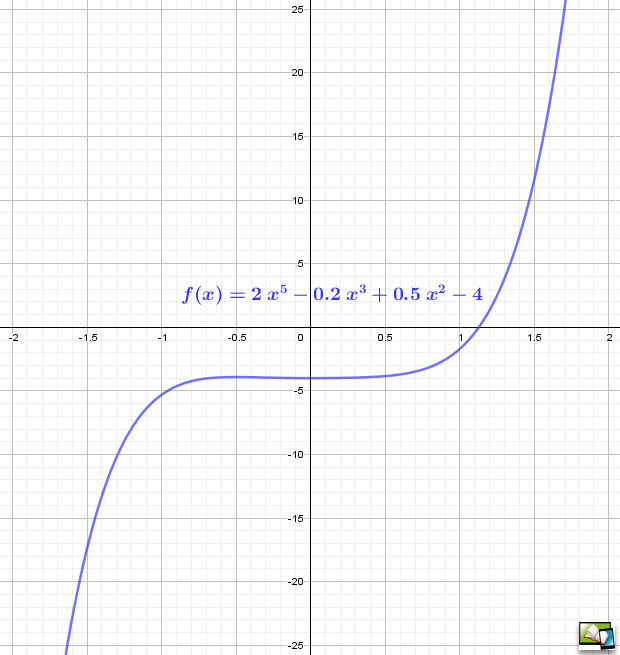
Der Definitionsbereich beinhaltet alle reellen Zahlen [`D(f) = RR` ] Die Funktion ist stetig, ihr Graph (siehe Beispiel) also zusammenhängend und der Bild- oder Wertebereich ist eine Teilmenge der reellen Zahlen oder alle reellen Zahlen.
`f` ist differenzierbar, sie besitzt also eine Ableitung `f'`, die wiederum ein Polynom ist mit einem um `1` verminderten Grad. Es gilt die Regel: `f'(x)= n·a_n*x^(n-1)+(n-1)*a_(n-1)*x^(n-2)+(n-2)*a_(n-2)x^(n-3)+ ... + 1*a_1x^0` mit `a_n != 0`
`f'(x)=sum_(i=1)^n i*a_i*x^(i - 1)` |
|
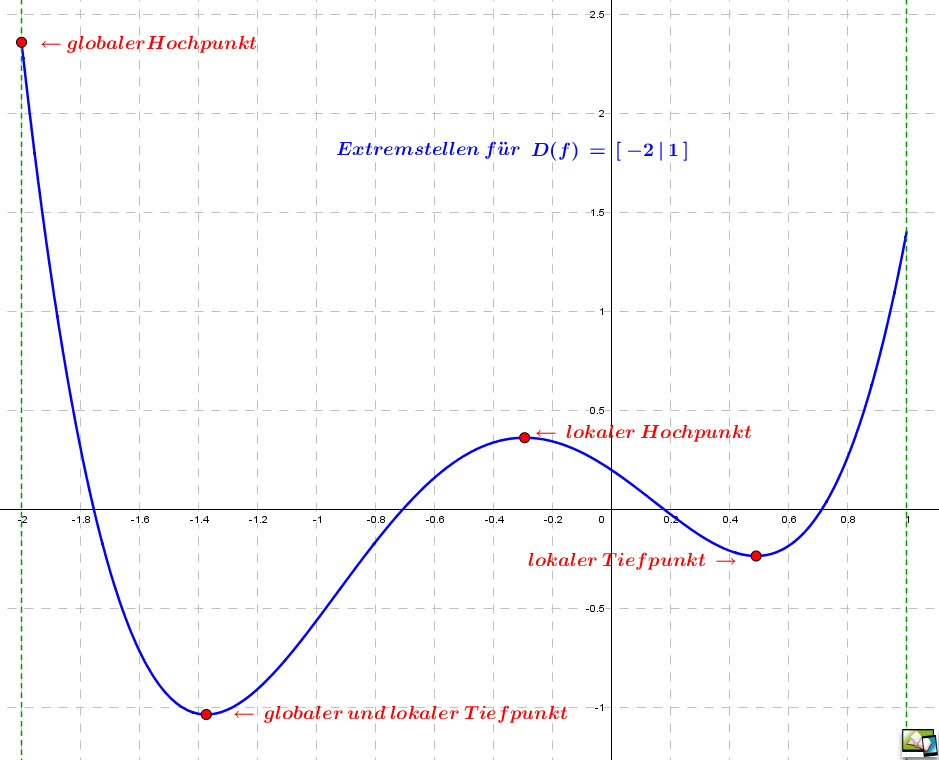
| Extrempunkte
Bei ganzrationalen Funktionen `f` werden in diesem Buch einzelne Punkte `(x|f(x))` im Definitionsbereich der Funktion als Extremstelle ( oder Extrempunkt/Extremum) bezeichnet, wenn ihr Funktionswert `f(x)` in einem lokalen Bereich (lokale Extremstelle) oder im gesamten Definitionsbereich (globale Extremstelle) einen höchsten oder niedrigsten (reellen) Wert besitzt. |
 |
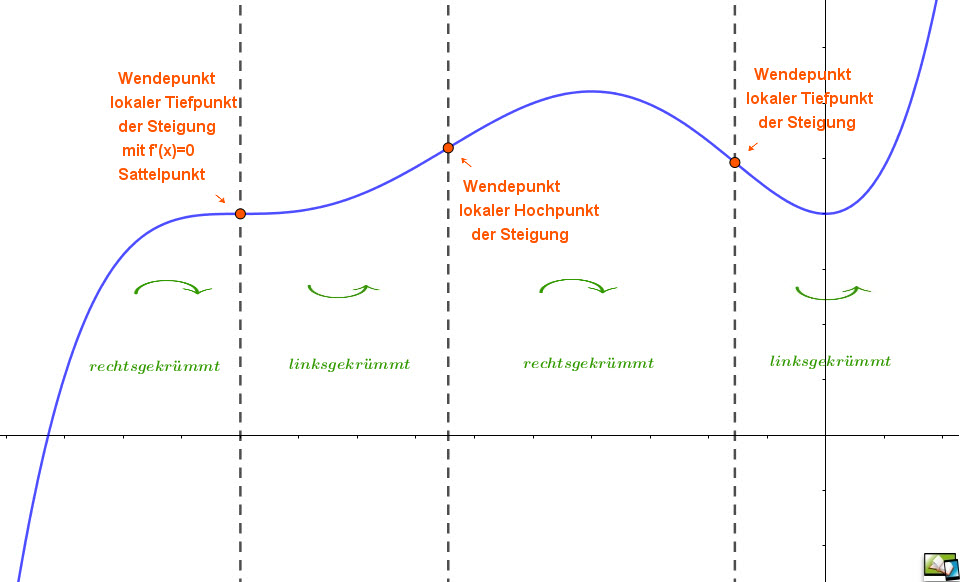
| Wendepunkte
Ein Punkt `W = (x|f(x))` auf dem Graphen einer ganzrationalen Funktion heißt Wendepunkt, wenn an dieser Stelle die Krümmung des Graphen von einer Rechts- in eine Linkskurve oder von einer Links- in eine Rechtskurve wechselt. Diese Punkte sind lokale Extremstellen der 1.Ableitung `f'` der Funktion, sie besitzen demnach die größte oder kleinste Steigung des Funktionsgraphen in einem lokalen Bereich. In einem Zusatzkapitel wird für den LK der Begriff "Krümmung in einem Punkt" eingeführt. Zusammenfassende Aufgaben, wie sie in Klausuren und Prüfungen üblich sind, finden Sie unter bbfb_index |
 |
| Extremwertaufgaben
Immer nur das Beste und das Schönste - keiner ist größer, keiner hat mehr! Auch da funktioniert Mathematik - zumindest, wenn man die Funktion kennt. In diesem Kapitel werden höchste und tiefste Funktionsstellen errechnet und interpretiert. |
|
| Steckbriefaufgaben
Obwohl der Begriff des "Steckbriefs" viel von seiner gerichtsladenden Bedeutung verloren hat, fühlen viele sich von Steckbriefaufgaben an mittelalterliche Justizmethoden erinnert. In diesem Kapitel wird versucht, diesem Gefühl ein wenig entgegenzuwirken. Im Mittelpunkt steht die Suche nach ganzrationalen Funktionen, deren Verhalten modellhaft funktionale Zusammenhänge in realen Situationen beschreiben kann. Mit Hilfe vorgegebener oder notwendiger Eigenschaften in Bezug auf Krümmung, Steigungsverhalten, Extrempunkten u.a. werden die Parameter solcher Funktionen bestimmt. |
 |
|
Hier finden Sie Modellierungs-Probleme zu Autobahntrassen, Sprungschanzen, Erdbeerwachstum, Hochwasser, Bezinverbrauch und vieles Andere mehr. |
|
|
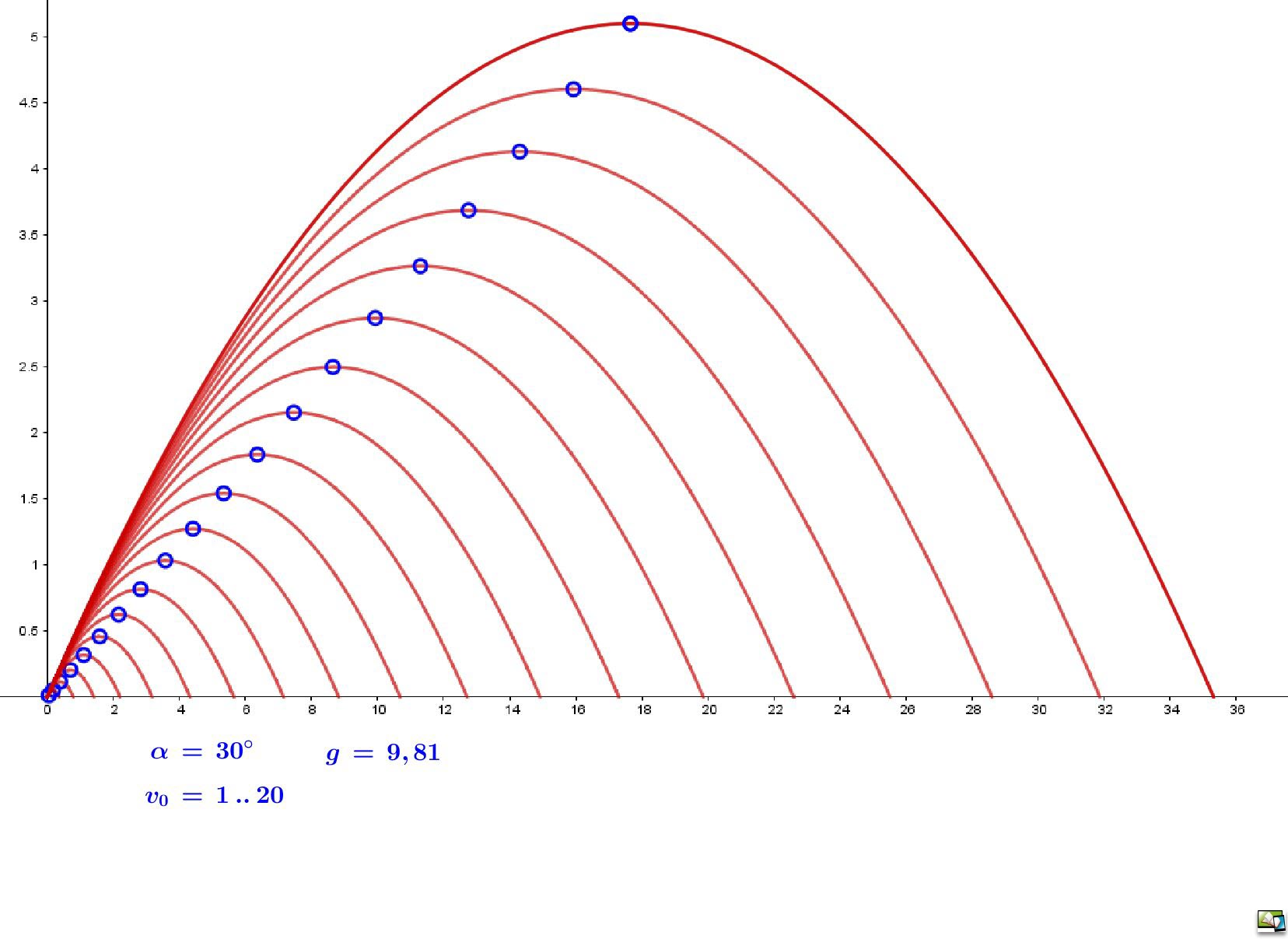
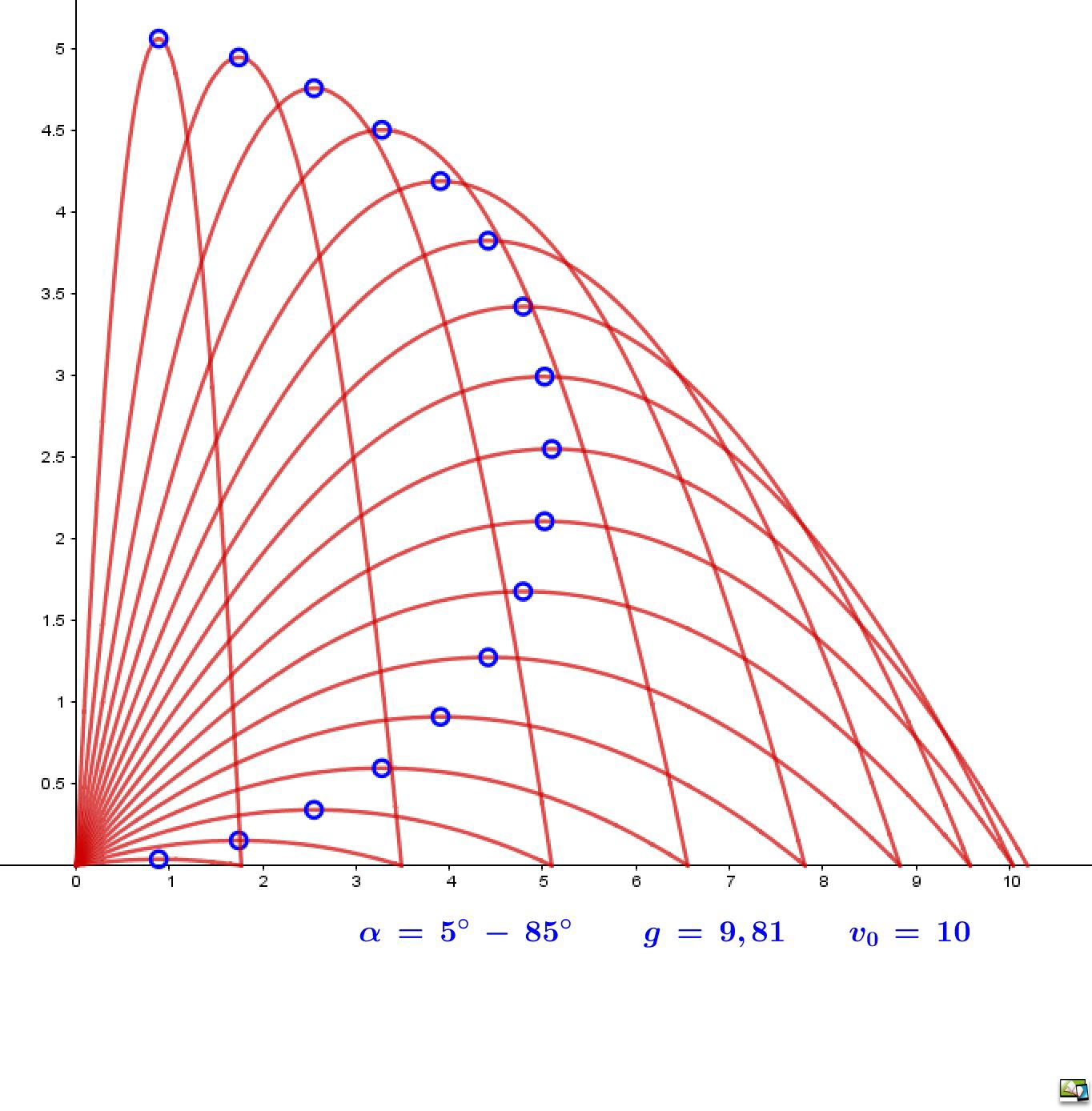
Eine Menge von Funktionen, die neben der Variablen (`x`) in ihrer Funktionsgleichung noch (eine) weitere Veränderliche - einen sogenannten Scharparameter (häufig `a`) - besitzen, bildet eine Funktionenschar, deren (gemeinsame) Eigenschaften durch verschiedene Werte dieses Parameters bestimmt werden. Wurfparabeln sind die Graphen der Funktionen, die entstehen, wenn man eine gleichmäßige (nach "schräg oben" gerichtete Bewegung) mit der Schwerkraft im freien Fall überlagert. Betrachten Sie die Veranschaulichungen in den Grafiken rechts. Ohne Berücksichtigung von evtl. Gasreibungen o.ä. ergibt sich eine Parabelschar, die durch die drei Parameter `v_0` [Abwurfgeschwindigkeit in `m/s`], den Abwurfwinkel `alpha` und der Schwerkraftbeschleunigung `g (m/s^2)` bestimmt wird und durch die Funktionsgleichungen `f_(v_0αg)(t)` = `- (g)/(2*v_0^2*cos^2(α))*t^2 + tan(α)*t` `(t >= 0`) berechnet werden kann. |
|
|
Zusammenfassung - Aufgaben zum Überblickswissen
Definition, Eigenschaften und Besonderheiten der ganzrationalen Funktionen / Polynome werden zusammenfassend aufgeführt. |
aus: Fricke-Heiland-Oppermann Mathematisches Unterrichtswerk Arithmetik und Algebra II 1947 |


 Kurzform
Kurzform