Quelle: https://nwm2.net-schulbuch.de/index.phpDruckversion vom 25.09.2023 17:38 Uhr
Startseite Qualifikationsphase Analysis Exponentialfunktionen
Exponentialfunktionen
| Einführung: Die EINE unter den Exponentialfunktionen
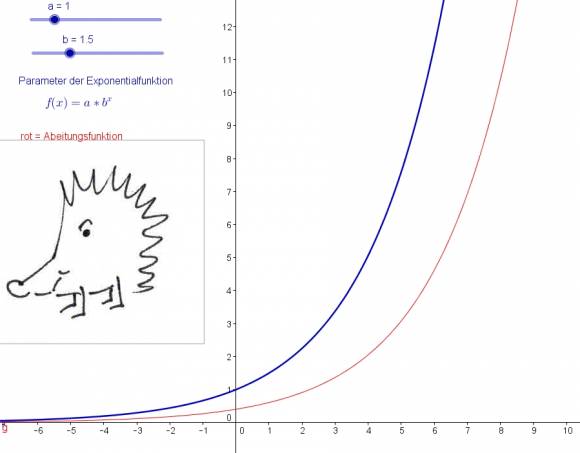
Hier geht es um die Ableitungsfunktionen von Exponentialfunktionen und im Zusammenhang damit um die besondere Basis e (Eulersche Zahl). |
 |
|
Kettenregel für Exponentialfunktionen Die (vereinfachte) Kettenregel gibt an, wie man zu Funktionen vom Typ `h(x) = a * e^(g(x))`die Ableitungsfunktionen bestimmt.
|
 |
|
Produktregel für Exponentialfunktionen Die zweite Regel, die man für die Ableitung (nicht nur) von Exponentialfunktionen braucht, heißt Produktregel. Sie wird immer dann angewendet, wenn eine Funktion als Produkt zweier Funktionen beschrieben werden kann: `h(x) = f(x) * g(x)`
|
 |
|
Wachstum kann sehr unterschiedlich verlaufen. Hier lernen Sie insbesondere lineare von exponentiellen und exponentielle von logistischen bzw. beschränkten Wachstumsprozesse zu unterscheiden. |
|
| Anwendungen
Reale Prozesse verlaufen zwar sehr selten nach strengen mathematischen Regeln. Allerdings kann man in einigen Fällen das Wachstum annähernd durch mathematische Funktionen beschreiben. Dadurch wird die Berechnung von Veränderungen etc. leichter möglich. |
 |
| Zusammenfassung und Selbsttest
|
