Druckversion vom 27.07.2024 10:38 Uhr
Startseite Qualifikationsphase Analysis LK: Funktionenscharen
LK: Funktionenscharen - Erforschen
Nutzen Sie möglichst die GeoGebra-App zur Darstellung in allen Kapiteln!
|
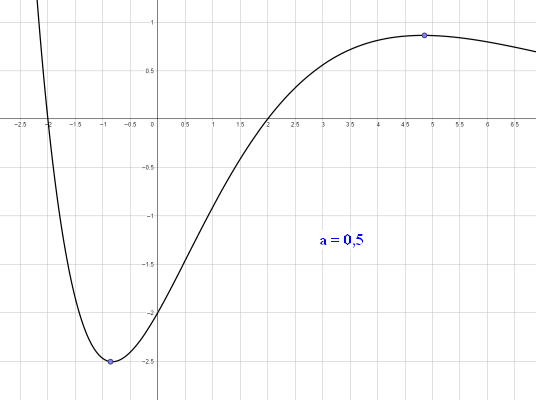
In der psychologischen Aufmerksamkeitsforschung nutzt man für die Interpretation von experimentellen Ergebnissen in der Beobachtung von hirnphysiologischen Parametern seit mehr als 150 Jahren auch mathematische Funktions-Modelle (vgl. z.B. Weber-Fechner-Gesetz aus dem 19.Jhdt.) zur Analyse der beobachteten Daten. In der Forschung von zeitabhängigen Verläufen der Aufmerksamkeitsdaten stellt das mathematische Funktionenmodell `f_a(x) = (6ax + 0.5)* e^(-1/ax) [a!=0]` eine solche Modellierung dar. Es beschreibt den Verlauf der Aufmerksamkeitsstärke (in nicht näher bezeichneten AE - Einheiten) innerhalb einer Zeitspanne von 0 bis n Stunden. Eine sehr grobe Vereinfachung der physiologischen Hintergründe könnte z.B. interpretiert werden als Verlauf der Aufmerksamkeit von Schülern während der ersten n-Stunden nach Unterrichtsbeginn.
Interpretieren Sie für die Fragestellungen den Nullpunkt der Zeit als 8.00 Uhr und wählen Sie n = 4. Untersuchen Sie in diesem Modell folgende Fragestellungen:
|
|
|
In der psychologischen Aufmerksamkeitsforschung nutzt man für die Interpretation von experimentellen Ergebnissen in der Beobachtung von hirnphysiologischen Parametern seit mehr als 150 Jahren auch mathematische Funktions-Modelle (vgl. z.B. Weber-Fechner-Gesetz aus dem 19.Jhdt.) zur Analyse der beobachteten Daten. In der Forschung von zeitabhängigen Verläufen der Aufmerksamkeitsdaten stellt das mathematische Funktionenmodell `f_a(x) = (6ax + 0.5)* e^(-1/ax) [a!=0]` eine solche Modellierung dar. Es beschreibt den Verlauf der Aufmerksamkeitsstärke (in nicht näher bezeichneten AE - Einheiten) innerhalb einer Zeitspanne von 0 bis n Stunden. Eine sehr grobe Vereinfachung der physiologischen Hintergründe könnte z.B. interpretiert werden als Verlauf der Aufmerksamkeit von Schülern während der ersten n-Stunden nach Unterrichtsbeginn.
Interpretieren Sie für die Fragestellungen den Nullpunkt der Zeit als 8.00 Uhr und wählen Sie n = 4. Untersuchen Sie in diesem Modell folgende Fragestellungen:
|
|
|
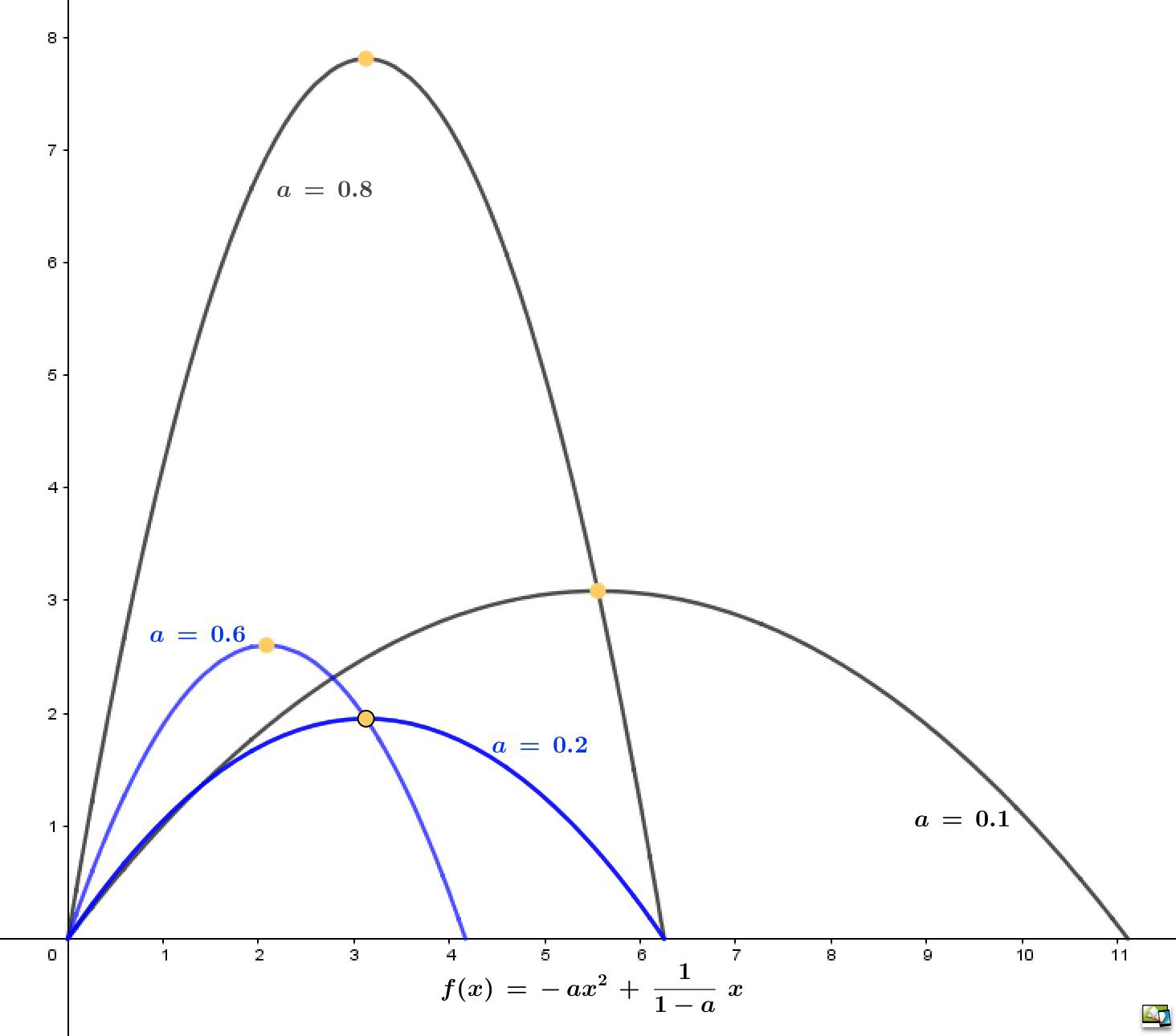
zu a. Um zu zeigen, dass `f(x) = (4,8x+0,5)*e^(-1.25x)` eine bestimmte Funktion der Modellfunktionen `f_a(x) = (6a + 0.5)* e^(-1/ax)` ist, muss ein entsprechendes a bestimmt werden. Aus dem 1.Faktor `4,8x + 0.5 = 6a + 0.5` berechnet sich `a = 4/5 = 0.8`. Eingesetzt in den zweiten Faktor `e^(-1/ax)` ergibt sich `e^(-1/0.8 x) = e^(-1.25x)`. Der Faktor `4,8x + 0,5` ist für alle Werte im Intervall `[0;4]` positiv. Der e-Funktionsfaktor ist immer positiv. `rArr f(x) > 0` für alle `x in [0;4]`. |
 |
|
zu b. Gesucht sind die absoluten Extremwerte im Intervall [0;4]. lokale Extrema: Mit der Produktregel ergibt sich:`f'(x) = 4,8*e^(-1.25x) + (4.8x + 0.5)*(-1.25)*e^(-1.25x)` `= (-6x + 4.175)* e^(-1.25x)` `f'(x) = 0 hArr 4.175 = 6x rArr x = 167/240 ~~ 0.696` Mit `f(0) = 0.5, f(167/240) ~~ 1.609` und `f(4) ~~ 0.133` ergibt sich, dass `P= (167/240 | f(167/240)` lokales und absolutes Maximum im Intervall `[0;4]` ist. Zusätzlich folgt, dass es kein lokales Minimum gibt und `Q = (4 | f(4) )` das absolute Minimum im Intervall ist. Diese Punkte lassen sich unter den Modellvoraussetzungen also als Werte der maximalen und minimalen Aufmerksamkeit bezeichnen. |
zu c. Gesucht sind die Punkte mit minimaler bzw. maximaler Steigung von f im Intervall. Zum Wendepunkt: Wieder nach der Produktregel ergibt sich: `f''(x) = (7,5x - 11,21875)*e^(-1.25x)` `f''(x) = 0 hArr x = 359/240 ~~ 1,496` Da `lim_(x->oo)f(x) = 0` wegen der Eigenschaft der e-Funktion gibt es einen Wendepunkt in `W = (359/240 | f(359/240) ~~ 0,592)`.Mit `f'(0) = 4,175`, `f'(359/240) ~~ 1.1839` und `f'(4) ~~ -0,134` gilt: Der stärkste "Aufmerksamkeitsanstieg" ist am Beginn des Intervalls bei x=0, der größte "Abfall der Aufmerksamkeit" ist im Wendepunkt der Funktion. |
|
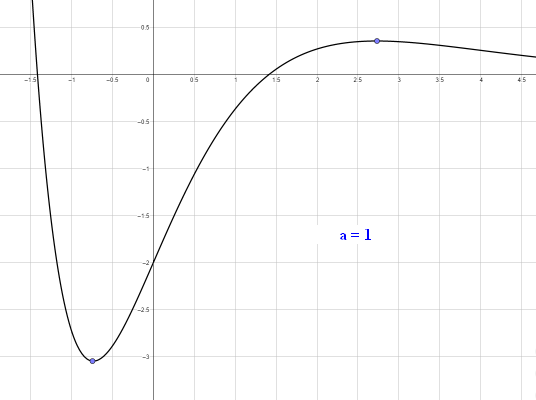
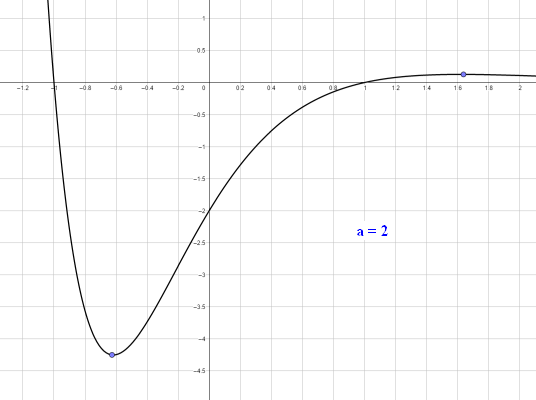
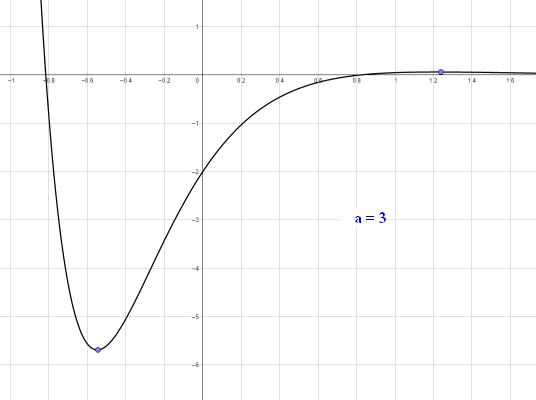
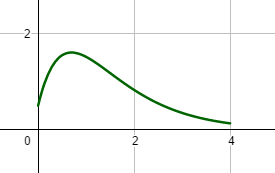
zu d. Der Faktor (6ax+0,5) bestimmt aufgrund der Eigenschaft einer e-Funktion das Vorzeichen und die Nullstelle `x_N = - 1/(12a)` der Funktionen `f_a`.Ein negativer Wert für a ist in diesem Modell aber nicht sinnvoll, denn dann gäbe es für alle x-Werte > nN nur exponentiell fallende negative Aufmerksamkeitswerte. Für alle x-Werte > xN gäbe es nur exponentiell fallende negative Aufmerksamkeitswerte. [Auch wenn eigene Beobachtungen kurz nach Unterrichtsbeginn ein solches Modell durchaus vollstellbar machen!] Für a>0 erlauben die relativ moderaten Anstiege und Zahlenwerte der Aufmerksamkeitswerte für a-Werte bis ca. 3 eine durchaus sinnvolle Interpretation des Geschehens. Größere a-Werte machen vor allem wegen der hohen Anstiegsgeschwindigkeit eine Interpretation kaum nachvollziehbar. Die absolute Größe der Werte könnte man im Modell durch geänderte Einheiten beeinflussen. |
 |
|
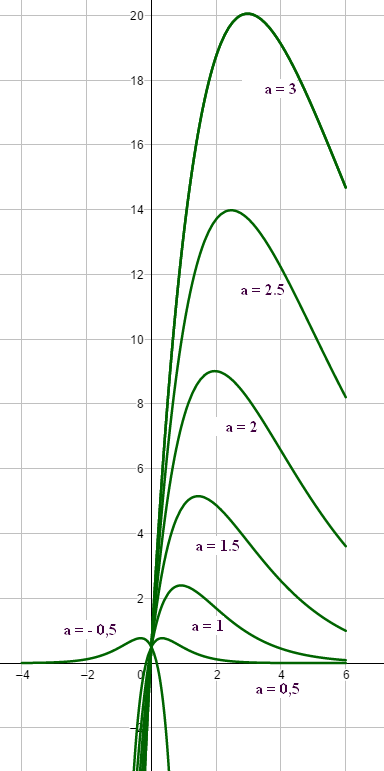
zu e. Die Berechnung des Maximalwertes aus dem Aufgabenteil b. für a=0,8 kann allgemein durchgeführt werden: Mit `f_a(x) = (6ax + 0.5)* e^(-1/ax)` gilt: [Produktregel] `f_a^'(x) = 6a * e^(-1/ax) + (6ax + 0.5)*(- 1/a)*( e^(-1/ax))` `= (6a - 6x - 1/(2a))* e^(-1/ax)` `= (-6x + (12a^2 - 1)/(2a))* e^(-1/ax)` `f_a^'(x) = 0 hArr (-6x + (12a^2 - 1)/(2a)) = 0` `rArr x = (12a^2 - 1)/(12a) = a - 1/(12a)` [für a=0.8 demnach `x = 0.8 - 1/(12*0.8) = 167/240` s.Teil b.] Aufgrund der Grenzwerteigenschaft der e-Funktion und der Existenz der Nullstelle im 2.Faktor handelt es sich jeweils um ein lokales und absolutes Maximum im Punkt `P = (a - 1/(12a) | 6a^2*e^(-1 + 1/(12a^2)))` Für die Aufgabenstellung, dass die maximale Aufmerksamkeit um 10.00 Uhr erreicht wird ist demnach a so zu berechnen, so dass `a - 1/(12a) = 2 rArr a^2 - 2a - 1/12 = 0` `a_(1,2) = 1 +- sqrt(13/12)` `rArr a_1 ~~ 2.041` und `a_2 ~~ -0.041`. Der negative a-Wert ist für die Modellierung nicht sinnvoll. [Der Aufmerksamkeitswert läge hier bei ca. 1,87·1019!]
|
 |
|
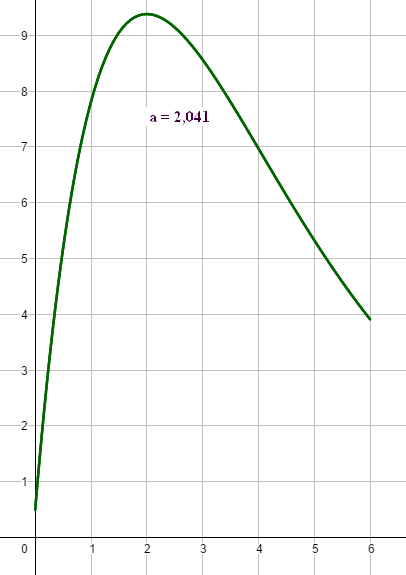
zu f. Ein Maß für dieGesamtaufmerksamtkeit in diesem Modellansatz könnte die Gesamtfläche unter der Aufmerksamkeitskurve, dem Graphen von fa, darstellen. Mit den bisher bestimmten Bedingungen der Funktionen ist daher zu berechnen: `int_0^n f_a(x) dx` Berechnung mit Hilfe der partiellen Integration :Aufgrund der Ableitungseigenschaft der e-Funktion und des linearen Faktors wählt man `u(x) = 6ax + 0.5` und `v'(x) = e^(-1/ax)`. Dann ergibt sich: `u'(x) = 6a` und `v(x) = -a*e^(-1/ax)`. `rArr int (6ax + 0.5)*e^(-1/ax) dx` `= (6ax + 0.5)*(-a*e^(-1/ax)) - int 6a*(-a*e^(-1/ax))dx` `= (6ax + 0.5)*(-a*e^(-1/ax)) - 6a^3*e^(-1/ax)` `= (-6a^2x - 6a^3 - 0.5a )*e^(- 1/ax) = F_a(x)` Probe
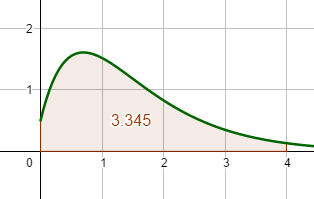
Berechnung der bestimmten Integrale für die ersten 4 Stunden: `a = 0.8` `int_0^4 (4.8x + 0.5)*e^(-1.25x) dx` `= F_0.8 (4) - F_0.8(0)` `= (-6*0.8^2*4 - 6*0.8^3 - 0.4 )*e^(- 5) ` `- (- 6*0.8^3 - 0.4 )*e^0` `~~ -0.127 - (- 434/125) ~~ 3.345` [AE]
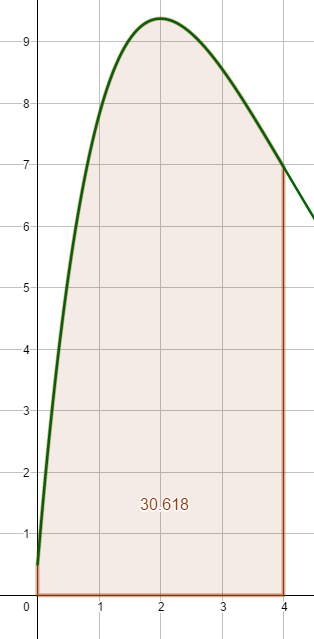
`a = 1 + sqrt(13/12)` `int_0^4 ((6+sqrt39)x + 0.5)*e^((12-2sqrt39)x) dx` `= F_(1 + sqrt(13/12))(4) - F_(1 + sqrt(13/12))(0)` `= (-6(1 + sqrt(13/12))^2*4 - 6(1 + sqrt(13/12))^3 - 0.5(1 + sqrt(13/12)) )*e^(- 1/(1 + sqrt(13/12))*4)` `- (-6(1 + sqrt(13/12))^2*0 - 6(1 + sqrt(13/12))^3 - 0.5(1 + sqrt(13/12)) )*e^(- 1/(1 + sqrt(13/12))*0)` `~~ -21.416 - (- 52.033) ~~ 30.617` [AE]
In wieweit die sehr ungleichen Größen der Gesamtaufmerksamkeit durch die zeitliche Verschiebung in dem Modell eine reale Entsprechung finden können, ist keine mathematische Fragestellung. |
|
|
`f_1(x) = x^3 - 6x^2`
|
|
Eine Schar von Funktionen wird definiert durch `f_a(x) = (ax^2 - 2)*e^(-ax) a in RR`
|
|
`f_1(x) = -0,25x^2 + 4/3x`
|
`f_1(x) = x^3 - 6x^2`
`f_2(x) = x^3 - 4x^2`
`f_3(x) = x^3 - 2x^2` und
`f_4(x) = x^3 `
sind die Funktionsgleichungen von Parabeln mit ähnlichen geometrischen Eigenschaften.
- Berechnen Sie Nullstellen, relative Extrema und Wendepunkte der Funktionen und skizzieren Sie die Graphen der Funktionen händisch in einem Koordinatensystem.
Formulieren Sie evtl. auffallende Gemeinsamkeiten. - Zeigen Sie kurz, dass alle Parabeln aus a. eine Funktionsgleichung der Form
`f_a(x) = x^3+6a*x^2` mit `a in [-1; 0] ` besitzen. - Nutzen Sie Ihren GTR, GeoGebra©, Excel© oder andere Hilfsmittel zur Darstellung möglichst vieler Parabelgraphen mit `a in RR`.
- Untersuchen Sie nun allgemein die Funktionsschar `f_a(x) = x^3+6a*x^2` mit `a in RR `.
Berechnen Sie dazu die Nullstellen, die relativen Extrema und die Wendepunkte der Funktionen. - Bestimmen Sie die Kurve, auf der die relativen Extrema liegen.
Bestimmen Sie auch die Kurve, auf der die Wendepunkte liegen.
|
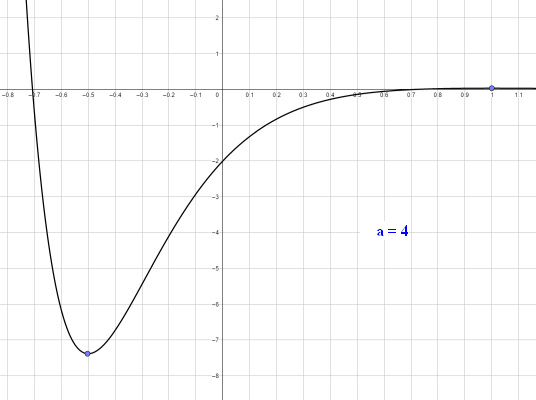
zu a. `f_1(x) = x^3-6x^2` Nullstellen: `(0|0)` und `(6|0)` relativer Hochpunkt, Tiefpunkt: `(0|0)` und `(4|-32)` Wendepunkt: `(2|-16)`
`f_2(x) = x^3-4x^2` Nullstellen: `(0|0)` und `(4|0)` relativer Hochpunkt, Tiefpunkt: `(0|0)` und `(8/3|-256/27) ~~ (8/3|-9,481)` Wendepunkt: `(4/3|-128/27) ~~ (4/3|-4,739)`
`f_3(x) = x^3-2x^2` Nullstellen: `(0|0)` und `(2|0)` relativer Hochpunkt, Tiefpunkt: `(0|0)` und `(4/3|-32/27) ~~ (4/3|-1,185)` Wendepunkt: `(2/3|-16/27) ~~ (2/3|-0,593)` `f_4(x)=x^3` Der Graph dieser Funktion hat in `(0|0)` einen Sattelpunkt.
|
 |
|
zu b. Für die Werte von a ergibt sich: `f_1 rArr a = -1` `f_2 rArr a = -2/3` `f_3 rArr a = -1/3` `f_4 rArr a = 0`
zu c. Abgebildet sind Graphen der Funktionen `f_a ` für a = -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5. |
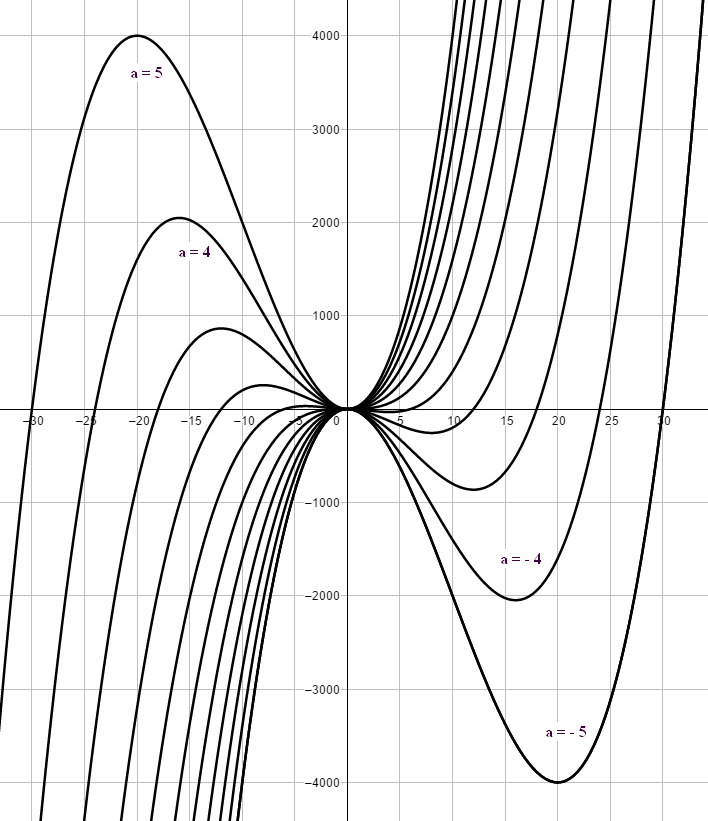 |
|
zu d. Ableitungen: `f_a^'(x) = 3x^2 + 12ax` `f_a^('')(x) = 6x + 12a` `f_a^(''')(x) = 6` Bestimmung der Nullstellen: `f_a(x)=0 iff x^3 + 6a*x^2=0 iff x^2*(x + 6a)=0` `=> x_1=0 ` und `x_2=-6a` Bestimmung der lokalen/relativen Extrema: Notwendig ist: `f_a^'(x) = 0` hier also `3x^2 + 12ax = 3x*(x + 4a) = 0` `=> x_1=0` und `x_2=-4a`
`x_1=0`: Es ist `f_a^('')(x) = 6x + 12a` `=> f_a^('')(0) = 12a` Fallunterscheidung: 1. Wenn `a>0`, liegt an der Stelle `0` ein Tiefpunkt vor. 2. Wenn `a<0`, liegt an der Stelle `0` ein Hochpunkt vor. 3. Wenn `a=0`, ist `f_a(x) = x^3` und diese Funktion hat in `N(0|0)` einen Sattelpunkt, also einen Wendepunkt mit der Steigung Null. Diese Punkte haben unabhängig von a die Koordinaten `K(0|0)`
`x_2 = -4a`: Es ist `f_a^('')(x) = 6x + 12a` `=> f_a^('')(-4a) = -12a` 1. Wenn `a>0`, liegt an der Stelle `-12a` ein Hochpunkt vor. 2. Wenn `a<0`, liegt an der Stelle `-12a` ein Tiefpunkt vor. 3. Wenn `a=0`, ist `f_a(x) = x^3` und diese Funktion hat in `N(0|0)` einen Sattelpunkt, also einen Wendepunkt mit der Steigung Null. (siehe oben) Diese Punkte haben die Koordinaten `E_a(-4a|32a^3)` Bestimmung der Wendepunkte: Notwendig ist: `f_a^('')(x) = 0` Hier also `6x + 12a =0 iff x = -2a` Weil `f_a^(''')(x) = 6 != 0` liegt hier auch ein Wendepunkt vor. Seine Koordinaten sind `W_a(-2a|16a^3)` |
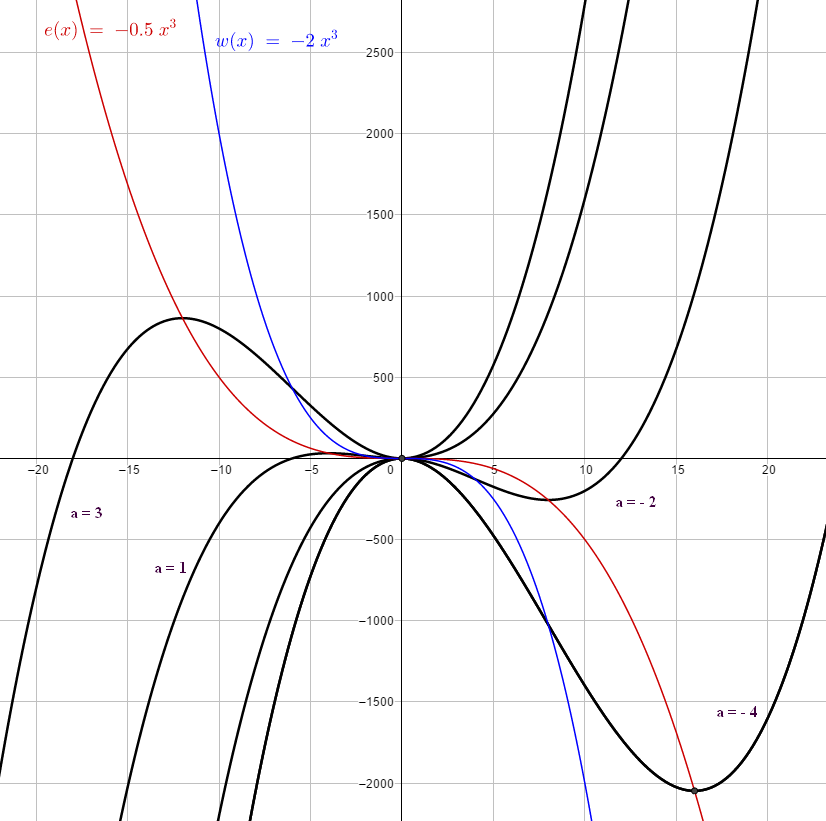
zu e. Die relativen Extrema haben die Koordinaten `E_a(-4a|32a^3)` Für den x-Wert gilt: `x = -4a iff a = -1/4x` Für die y-Koordinate gilt: `y = 32a^3` also gilt: `y = 32*(-1/4x)^3 = -1/2x^3` Die relativen Extrema liegen auf dem Graphen der Funktion `e(x) = -1/2x^3`
Die Wendepunkte haben die Koordinaten `W(-2a|16a^3)` Für den x-Wert gilt: `x = -2a iff a = -1/2x` Für die y-Koordinate gilt: `y = 16a^3` also gilt: `y=16*(-1/2x)^3 = -2x^3` Die Wendepunkte liegen auf dem Grafen der Funktion `w(x) = -2x^3`
|
Eine Schar von Funktionen wird definiert durch
`f_a(x) = (ax^2 - 2)*e^(-ax) a in RR`
- Zeigen Sie, dass alle Funktionsgraphen einen gemeinsamen Punkt besitzen. Untersuchen Sie, für welche Werte von a die Funktionen Nullstellen besitzen und geben Sie einen Berechnungsterm für diese Nullstellen an.
- Berechnen Sie mit Hilfe der 1. und 2.Ableitungsfunktionen die lokalen Extremstellen und notieren Sie dabei, für welche Werte von a sie existieren.
- Begründen Sie durch eine geeignete Rechnung, dass `f_(-1)(x)` keinen Wendepunkt besitzt und geben Sie einen allgemeinen Term für die Berechnung von Wendepunkten in Abhängigkeit von a an.
|
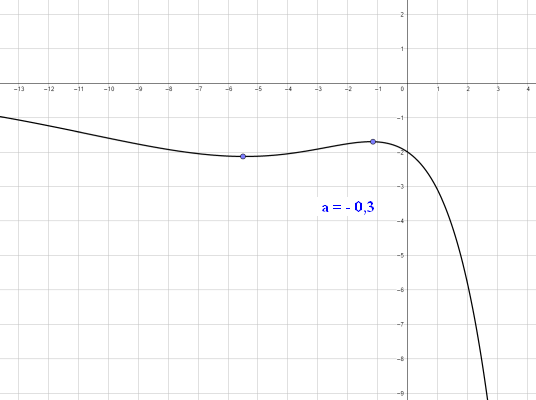
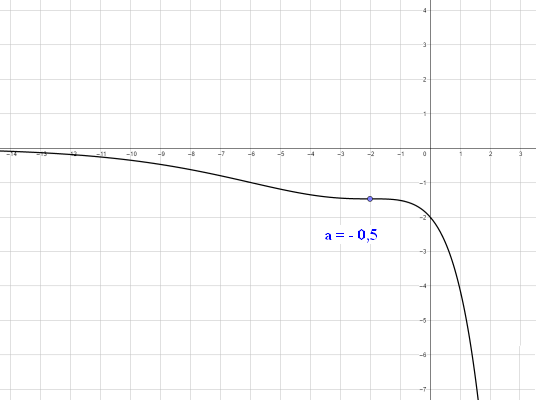
zu a. Für a = 0 handelt es sich um die Gerade y = -2. * Für alle Funktionsgraphen der Schar gilt: `f_a(0) = -2`. (0 | -2) ist also ein gemeinsamer Punkt aller Graphen. Nullstellenberechnung: Bei den Funktionsgleichungen handelt es sich jeweils um ein Produkt. Demnach muss mindestens ein Faktor des Produkts 0 sein, damit der Funktionsgraph dort eine Nullstelle besitzt. Der e-Funktions-Faktor kann aufgrund der Eigenschaft `e^x > 0 x in RR` nie Null sein. Zu untersuchen ist also der 2.Faktor `ax^2 - 2`: `ax^2 - 2 = 0 hArr x_(1,2) = +-sqrt(2/a)` ⇒ Für a <= 0 existiert keine Nullstelle, alle anderen Funktion besitzen die zwei Nullstellen `+-sqrt(2/a)`. |
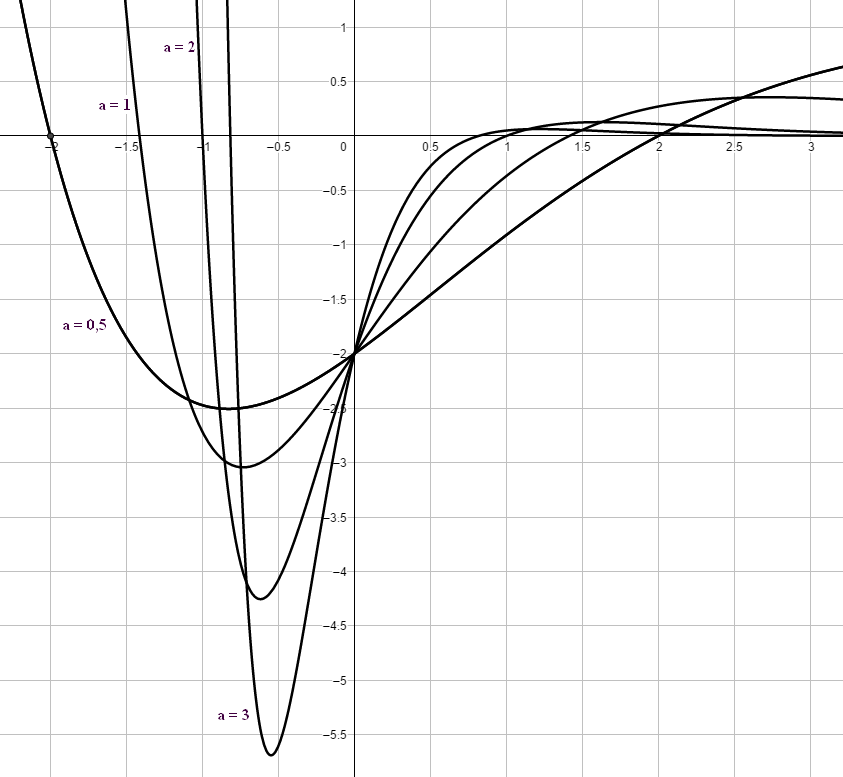 |
|||||||||||||||
|
zu b. Zu beachten ist, dass sich der Parameter a wie eine Zahl bei der Ableitung verhält. Mit der Produkt-Regel gilt:`f_a^'(x) = 2ax*e^(-ax) + (ax^2 - 2)*(-a)*e^(-ax)` `= (-a^2x^2 + 2ax + 2a)*e^(-ax)`
`f_a^'(x) = 0 hArr -a^2x^2 + 2ax + 2a = 0` `rArr x^2 - 2/ax - 2/a = 0` `rArr x_(1,2) = 1/a +- sqrt(1/(a^2) + 2/a) ` `= 1/a +- sqrt((1 + 2a)/(a^2)) ` `= 1/a +- 1/a*sqrt(1 + 2a) = 1/a*( 1 +- sqrt(1 + 2a))` `rArr` 2 Nullstellen existieren, falls `1 + 2a > 0 hArr a > -0.5`. Für a = -0.5 existiert genau eine Nullstelle bei x = -2. Für a < -0,5 gibt es keine Nullstellen der 1.Ableitungen, demnach auch keine lokalen Extrempunkte.
Grenzwertbetrachtung: für a > 0 : Es gilt aufgrund der Eigenschaften der e-Funktion: `lim_(x-> +oo)e^(-ax) = 0` und `lim_(x-> -oo)e^(-ax) = +oo` und `lim_(x-> +-oo)(ax^2 - 2) = +oo` Aufgrund der Dominanz der e-Funktion, * und der existierenden Nullstellen (s.a.) gilt daher: `rArr lim_(x-> +oo)f_a(x) = 0` [`darr` "von oben" ] und `rArr lim_(x-> -oo)f_a(x) = +oo` `1/a*( 1 + sqrt(1 + 2a)) > 0` ist eine Stelle mit einem lokalen Hochpunkt und `1/a*( 1 - sqrt(1 + 2a)) < 0` ist eine Stelle mit einem lokalen Tiefpunkt. für a < 0 : `lim_(x-> -oo)e^(-ax) = 0` `lim_(x-> +oo)e^(-ax) = +oo` und `lim_(x-> +-oo)(ax^2 - 2) = -oo` Es gilt daher: `rArr lim_(x-> +oo)f_a(x) = - oo` und `rArr lim_(x-> -oo)f_a(x) = 0` [`uarr` "von unten" ] Analog zur Betrachtung oben [jetzt keine Nullstelle] gilt demnach für -0,5 < a < 0: `1/a*( 1 + sqrt(1 + 2a)) < 0` ist eine Stelle mit einem lokalen Tiefpunkt und `1/a*( 1 - sqrt(1 + 2a)) < 0` ist eine Stelle mit einem lokalen Hochpunkt. Für den Sonderfall a = -0,5 besitzt `f_(-0.5)^'(x)`eine doppelte Nullstelle, `f_(-0.5)` hat demnach in -2 einen Sattelunkt, einen Wendepunkt mit der Steigung 0. Zusammenfassung:
|
|
|||||||||||||||
|
zu c. Es gilt: `f_a^('')(x) = (-2a^2x + 2a)*e^(-ax) + (-a^2x^2 + 2ax + 2a)*(-a)*e^(-ax)` `= (a^3x^2 - 4a^2x - 2a^2 + 2a)*e^(-ax)` `f_a^('')(x) = 0 hArr a^3x^2 - 4a^2x - 2a^2 + 2a = 0` `rArr x^2 - 4/ax - 2/a + 2/(a^2) = 0` `rArr x_(1,2) = 2/a +- sqrt(4/(a^2) + 2/a - 2/(a^2))` ` = 2/a +- sqrt(2/(a^2) + 2/a)` ` = 2/a +- 1/a*sqrt(2 + 2a)` ` = 1/a * (2 +- sqrt(2 + 2a))` Für a > -0,5 müssen aufgrund der existierenden lokalen Extrempunkte und der Grenzwerte in b. jeweils zwei Wendepunkte existieren. Die Wendestellen lassen sich demnach mit dem obigen Term berechnen. Für `a = -1` gilt ` f_-1^('')(x) = 0 rArr x = -2` als einzige Lösung. Es kann sich nicht um eine Wendestelle handeln, da `lim_(x-> -oo)f_a(x) = uarr 0` und es kein lokales Extremum (und keine Nullstelle) gibt. Für -1 < a < -0,5 existieren an den o.a. Stellen Wendepunkte. |
||||||||||||||||
`f_1(x) = -0,25x^2 + 4/3x`
`f_2(x) = -0,4x^2 + 5/3x`
`f_3(x) = -0,1x^2 + 10/9x` und
`f_4(x) = - 0,8x^2 + 5x`
sind vier Funktionsgleichungen von Parabeln mit ähnlichen geometrischen Eigenschaften.
- Berechnen Sie Nullstellen und Scheitelpunkt der Parabeln und skizzieren Sie die Graphen der vier Parabeln händisch in einem Koordinatensystem.
Formulieren Sie evtl. auffallende Gemeinsamkeiten. - Zeigen Sie kurz, dass alle Parabeln aus a. eine Funktionsgleichung der Form `f_a(x) = -ax^2+1/(1-a)*x` mit `a in (0; 1) ` besitzen.
- Nutzen Sie Ihren GTR, GeoGebra©, Excel© oder andere Hilfsmittel zur Darstellung möglichst vieler Parabelgraphen aus b.
- Berechnen Sie mit Hilfe der bekannten mathematischen Methoden die Werte für a, für den die Parabel die geringste Entfernung zwischen den Nullstellen besitzt und für den der Scheitelpunkt den kleinsten Funktionswert besitzt.
- Untersuchen Sie, ob es mehrere a - Werte gibt, die zu den gleichen Nullstellen oder Scheitelpunkten führen.
- Zeigen Sie, dass der Scheitelpunkt von `f_0.1` auf dem Graphen von `f_0.8` und der Scheitelpunkt von `f_0.2` auf dem Graphen von `f_0.6` liegt.
Geben Sie eine allgemeine Lösung dafür an, dass der Scheitel von `f_(a1)` auf dem Graphen von `f_(a2)` liegt.
|
zu a. `f(x) = -0,25x^2 + 4/3x` ⇒ f(x) = 0 ⇔ x = 0 v x = `16/3` ⇒ Scheitelpunkt in x=`8/3` und f(x) = `16/9` `f(x) = -0,4x^2 + 5/3x` ⇒ f(x) = 0 ⇔ x = 0 v x = `25/6` ⇒ Scheitelpunkt in x=`25/12` und f(x) = `125/72` `f(x) = -0,1x^2 + 10/9x` ⇒ f(x) = 0 ⇔ x = 0 v x = `100/9` ⇒ Scheitelpunkt in x=`50/9` und f(x) = `250/81` `f(x) = - 0,8x^2 + 5x` ⇒ f(x) = 0 ⇔ x = 0 v x = 6,25 ⇒ Scheitelpunkt in x=3,125 und f(x) = 7,8125
zu b. `f(x) = -0,25x^2 + 4/3x = - 1/4x^2 + 1/(3/4)x` `= - 1/4x^2 + 1/(1 - 1/4)x rArr a = 0.25` `f(x) = -0,4x^2 + 5/3x = - 2/5x^2 + 1/(3/5)x` `= - 2/5x^2 + 1/(1 - 2/5)x rArr a = 0.4` `f(x) = -0,1x^2 + 10/9x = - 1/10x^2 + 1/(9/10)x` `= - 1/10x^2 + 1/(1 - 1/10)x rArr a = 0.1` `f(x) = - 0,8x^2 + 5x = - 4/5x^2 + 1/(1/5)x` `= - 4/5x^2 + 1/(1 - 4/5)x rArr a = 0.8` |
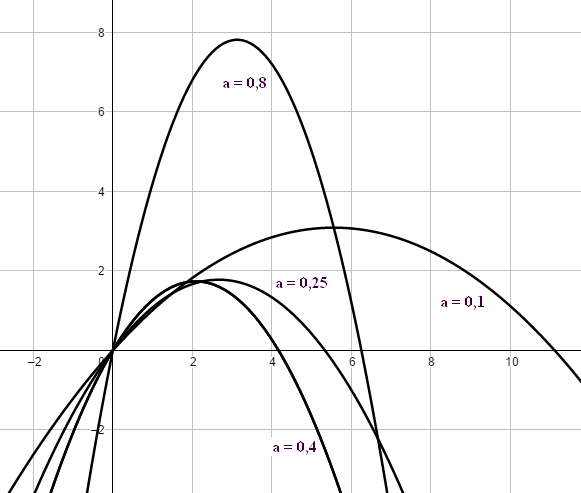 |
|
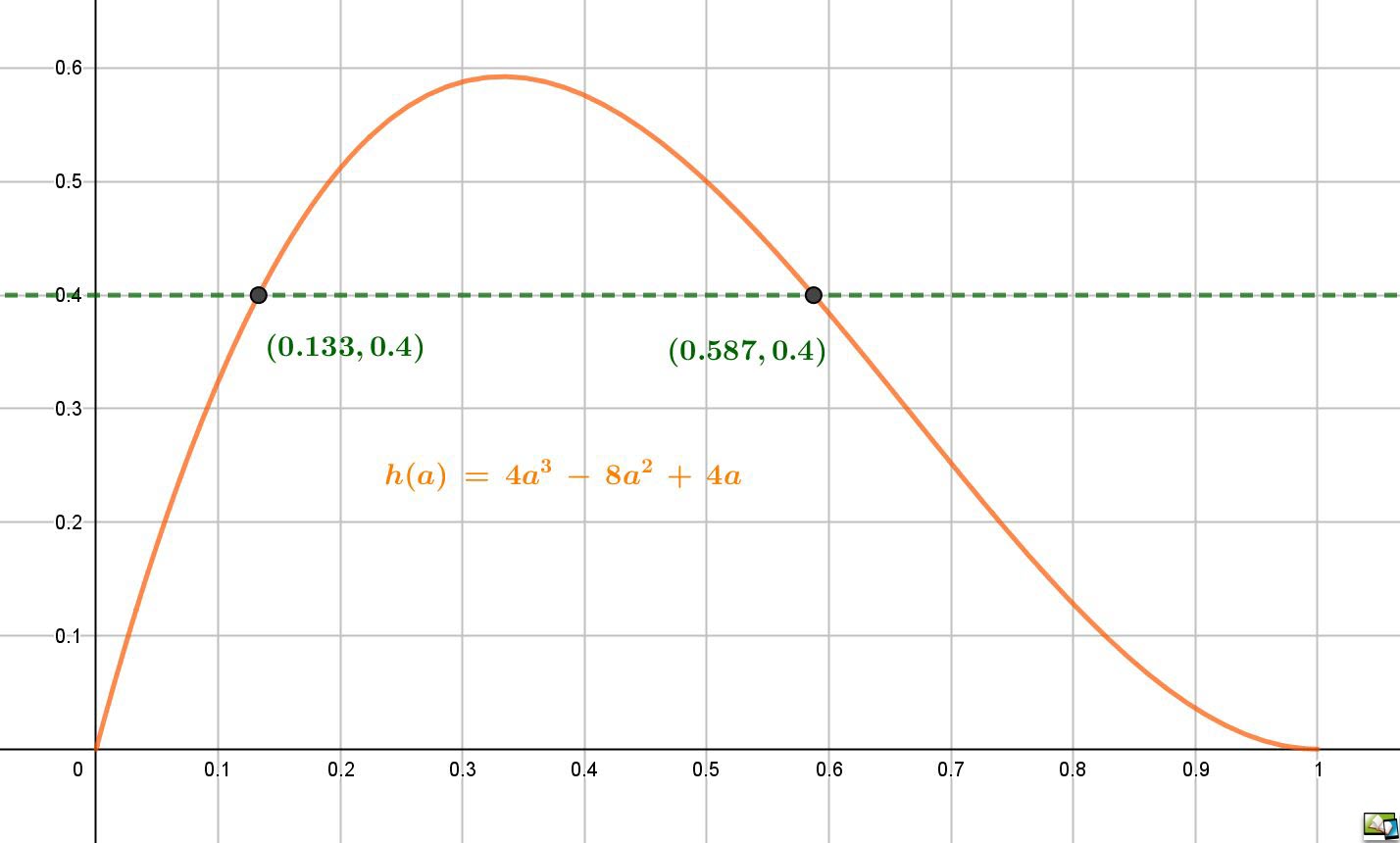
zu d. `f_a(x) = -ax^2+1/(1-a)*x` mit `a in [0; 1] ` Nullstellenberechnung: `f(x) = 0 iff -ax^2+1/(1-a)*x = 0` `iff x_1=0` und `x_2 = 1/(a*(1-a)) = 1/(a-a^2)` Damit der Abstand zwischen der Nullstelle (0|0) und der 2.Nullstelle möglichst klein ist, muss der Wert des Nenners möglichst groß sein. Gesucht ist demnach ein absoluter Hochpunkt von `g(a)= a-a^2`. Der Graph von g(a) ist wiederum eine nach unten geöffnete Parabel mit den Nullstellen 0 und 1. ⇒ Der Scheitel (0,5 | 0,25) ist lokaler und globaler Hochpunkt. ⇒ Für a = 0,5 ist der Abstand der beiden Nullstellen von f minimal und beträgt `1/(0,25) = 4`. Scheitelpunktberechnung: Da f eine nach unten geöffnete Parabel ist, liegt der x-Wert ihres Scheitelpunktes auf der Mitte der x-Werte der Nullstellen, also bei `x_E = 1/(2a(1-a))`. Es ist `f(1/(2a(1-a))) = 1/(4a*(1-a)^2)` Analog zur Nullstellenentfernung voneinander ist dieser Wert genau dann minimal, wenn der Nenner des Bruches am größten ist. Gesucht ist demnach ein globaler HP der Funktion Es ist `h(a) = 4a^3 - 8a^2 +4a` ein Polynom 3.Grades. `h´(a) = 12a^2 - 16a + 4` `h´(a) = 0 iff a^2 - 4/3a + 1/3= 0` `=> a_(1,2) = 2/3 +- sqrt (1/9) => a_1 = 1` und `a_2 = 1/3` `h´´(a) = 24a - 16 => h´´(1/3) = -8 < 0 =>` lok.HP in `a_2`. Da `h(0)=h(1)=0 => (1/3 | h(1/3)) = (1/3|16/27)` ist auch globaler HP. ⇒ Der minimale Funktionswert für den Scheitelpunkt wird bei `a=1/3` erreicht und beträgt `27/16`= 1,6875. |
zu c.
|
|
zu e. Die Nullstellenwerte entstanden aus den Werten der quadratischen Parabel `g(a)= a-a^2`. Aufgrund der Symmetrie zur Senkrechten zur x-Achse durch den Scheitelpunkt ergeben die Werte a und 1-a jeweils denselben Funktionswert und damit entehen für fa und f1-a dieselben Nullstellen.
Die Scheitelpunktfunktionswerte entstanden aus der Funktion `h(a) = 4a^3 - 8a^2 +4a` mit dem lokalen und globalen HP `(1/3 | 16/27)`. Da h(0) = h(1) = 0 sind und kein weiterer Extrempunkt im Intervall [0;1] vorhanden ist, kommt jeder Funktionswert y mit `0 ≤ y < 16/27` zweimal als Funktionswert im Intervall vor. Die genaue Berechnung führt zu der Gleichung dritten Grades `a*(a-1)^2 = 0.25y`. [z.B. für `y = 0.4 rArr a_1 ~~ 0.133` und `a_2 ~~ 0.587`]. |
|
|
zu f. `f_(1,2)(x) = -0,1·x^2 + 10/9x` mit dem Scheitelpunkt (s.a.) `(50/9 | 250/81)` `f_0.8(x) = -0.8x^2 + 5x ⇒ f_0.8(50/9)` `= -0,8*(50/9)^2 + 5*50/9 = 250/81` `f_0.2(x) = -0.2·x^2 + 1.25x` mit dem Scheitelpunkt (s.c.) `(3.125| 1.953125)` `f_0.6(x) = -0.6x^2 + 2.5x rArr f_0.6(3.125)` `= -0.6 *3,125^2 + 2.5*3.125 = 1.953125`
`f_(a1)(x) = - a_1x^2 + 1/(1-a_1)x` besitzt den Scheitelpunkt (s.c.) `(1/(2*a_1*(1-a_1)) | 1/(4*a_1*(1-a_1)^2))` `f_(a2)(x) = - a_2x^2 + 1/(1-a_2)x` ist die Funktionsgleichung einer zweiten dieser Parabeln. Damit der Scheitelpunkt von `f_(a1)` ein Punkt des Graphen von `f_(a2)` ist, muss `f_(a2) (1/(2*a_1*(1-a_1)))` `= 1/(4*a_1*(1-a_1)^2)` sein. Die folgende Gleichung ist demnach nach `a_2` aufzulösen: `1/(4*a_1*(1-a_1)^2)` = `- a_2* 1/(2*a_1*(1-a_1))^2 + 1/(1-a_2) * 1/(2*a_1*(1-a_1))` Multiplikation mit `4·a_1*(1-a_1)` ergibt: `1/(1-a_1)` `= - a_2* 1/(a_1*(1-a_1)) + 2/(1-a_2)` Multiplikation mit `(1-a_1)` : `1 = - a_2* 1/(a_1) + 2*(1-a_1)/(1-a_2)` Multiplikation mit `(1-a_2)` : `1-a_2 = - a_2* 1/(a_1)*(1-a_2) + 2 -2a_1` Ausmultiplizieren und ordnen: `1/(a_1) * a_2^2 + (1 - 1/(a_1))*a_2 + 1 -2a_1 = 0` ` hArr a_2^2 + (a_1 - 1)*a_2 + a_1 -2a_1^2 = 0` ` rArr a_(2(1,2)) = 1/2 (1-a_1) +- sqrt (1/4 (1-a_1)^2 + 2a_1^2 - a_1)` `= a_(2(1,2)) = 1/2 (1-a_1) +- sqrt (1/4 - a_1/2 + (a_1^2 )/4 + 2a_1^2 - a_1)` `= a_(2(1,2)) = 1/2 (1-a_1) +- sqrt ( 9/4 a_1^2 - 3/2 a_1 + 1/4)` `= a_(2(1,2)) = 1/2 (1-a_1) +- sqrt ( 1/4*(9a_1^2 - 6 a_1 + 1))` `= a_(2(1,2)) = 1/2 (1-a_1) +- sqrt ( 1/4*(3a_1 - 1)^2)` ` = a_(2(1,2)) = 1/2 (1-a_1) +- 1/2*(3a_1 - 1)` = `a_1` oder `1-2a_1` Damit eine Funktion aus der beschriebenen Schar entsteht, muss `1-2a_1 > 0` sein, d.h. es gilt für `a_1 < 0,5`. |
|