Druckversion vom 27.07.2024 10:09 Uhr
Startseite Qualifikationsphase Analysis Integralrechnung
Integralrechnung
Wie in der Differentialrechnung mit dem Tangentenproblem und der Momentangeschwindigkeit gibt es auch für die Integralrechnung zwei aus Anwendungen gewonnene Motivationen:
1. Die Berechnung von krummlinig begrenzten Flächen
2. Aus bekannten Änderungsraten (Zufluss, Abfluss, Verbrauch, Wachstum, ...) Werte für die zugrunde liegenden Größen zu bestimmen.
Flächenberechnungen werden seit der Antike untersucht. 500 Jahre vor Christus wurden in Griechenland Flächeninhalte mittels enthaltener oder überdeckender Vielecke abgeschätzt. Man konnte durch diese Methode sowohl Flächeninhalte als auch Volumina einiger einfacher Körper bestimmen. Archimedes (287–212 v. Chr.) verbesserte diesen Ansatz, und es gelang ihm, das Verhältnis von Kreisumfang zum Durchmesser `pi` als Wert zwischen `3 (10)/71` und `3 (10)/70` anzunähern. Johannes Kepler benutzte in seinem Werk Astronomia Nova (1609) bei der Berechnung der Marsbahn Methoden, die wir heute als numerische Integration bezeichnet würden. Er versuchte auch den Rauminhalt von Weinfässern zu berechnen (Keplersche Fassregel, 1615).
Die Integralrechnung kann man auch als die "Umkehrung" der Differentialrechnung auffassen, die von Isaac Newton und Gottfried Wilhelm Leibniz entwickelt wurde.
| Einführung
In diesem Kapitel werden Änderungsraten untersucht und damit ein erster Zugang zur Integralrechnung geschaffen. Grundlegende Begriffe werden eingeführt und Verbindungen zur Differentialrechnung vorbereitet. |
 |
| Stammfunktion/Integral
Die Zusammenstellung der im Einführungskapitel behandelten Beispiele führt auf den Zusammenhang zwischen Integral- und Differentialrechnung und macht die Einführung des Stammfunktionsbegriffs erforderlich. Auch wird der Unterschied zwischen Integral- und Stammfunktion thematisiert. |
 |
|
In diesem Kapitel wird der Zusammenhang zwischen Differential- und Integralrechnung untersucht. Mit dem Hauptsatz, der auf 2 Arten bewiesen wird, steht ein mächtiges Instrument zur Berechnung von Integralen zur Verfügung. |
 |
|
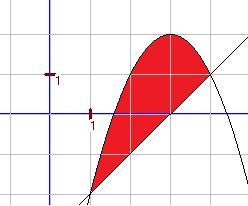
In diesem Kapitel werden Anwendungen der Integralrechnung, aber auch rein mathematische Flächenberechnungen behandelt. |
 |
|
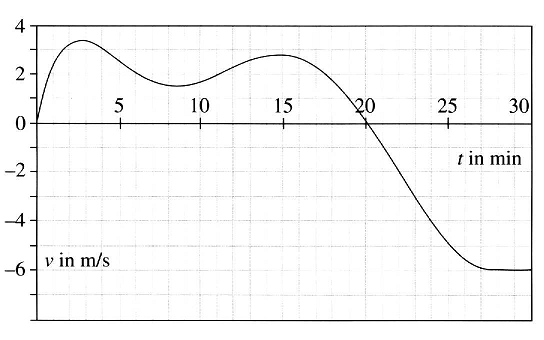
In diesem Kapitel werden einfache, aber auch sehr komplexe Anwendungen der Integralrechnung aus verschiedenen Sachbereichen behandelt. |
 |
|
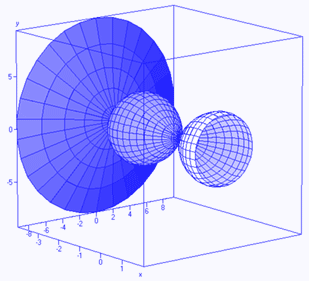
Rotationskörper wird ein Körper genannt, dessen Oberfläche durch Rotation einer erzeugenden Kurve um eine Rotationsachse gebildet wird. Die Kurve und die Rotationsachse liegen in der selben Ebene. Rotationskörper kommen auch im täglichen Leben vor (Weinglas, Rettungsring). In diesem Kapitel werden Volumen von Rotationskörpern bestimmt. |
 |
|
Ein Radfahrer fährt mit unterschiedlichen Geschwindigkeiten - welches ist seine Durchschnittsgeschwindigkeit? |
 |
|
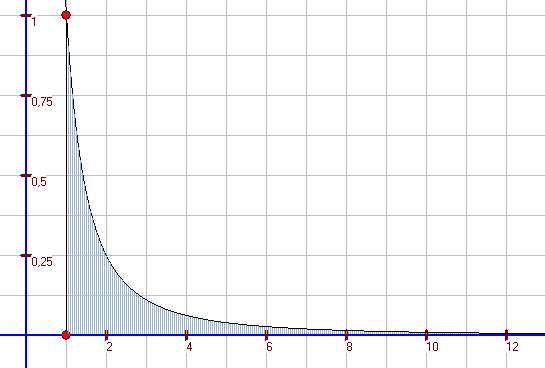
Haben unendlich ausgedehnte Flächen auch einen unendlich großen Flächeninhalt? Eine Antwort auf diese Frage finden Sie in diesem Kapitel. |
 |
|
LK: Partielle Integration und Substitution (optional) Eine Fülle von Funktionen, die Sie kennengelernt haben, ist mit den bisher behandelten Integrationsverfahren nicht aufleitbar. In diesem Kapitel lernen Sie weitere Integrationsverfahren kennen: die partielle Integration (das Gegenstück zu der Produktregel der Differentialrechnung), die Integration durch Substitution (in einer speziellen Form das Gegenstück zur Kettenregel der Differentilarechnung) und die logarithmische Integration als Sonderfall der Integration durch Substitution. |
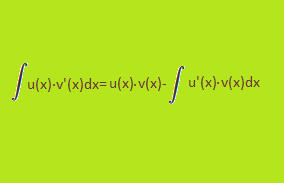 |
|
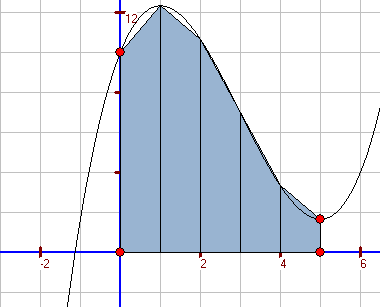
Numerische Integration (optional) In vielen Fällen kann ein bestimmtes Integral nicht berechnet werden, weil keine Stammfunktion bekannt ist. Dann kommen Näherungsverfahren zum Einsatz, von denen in diesem Kapitel zwei sehr effektive Verfahren genauer erläutert werden - das Sehnentrapez- und das Simpson-Verfahren. Ein weiteres Problem ist die Bestimmung von Kurvenlängen (Bogenlängen), bei dem ebenfalls ein Näherungsverfahren zum Einsatz kommt. Dabei wird auch der Zusammenhang zur Integralrechnung aufgezeigt. |
 |
|
LK: Integration durch Partialbruchzerlegung (optional) Hier wird die Integration gebrochen rationaler Funktionen mit einem quadratischen Nenner untersucht. Im Rahmen einer Vertiefung werden auch kubische Nenner betrachtet. Eine Langzeitaufgabe stellt eine besondere Herausforderung dar. |
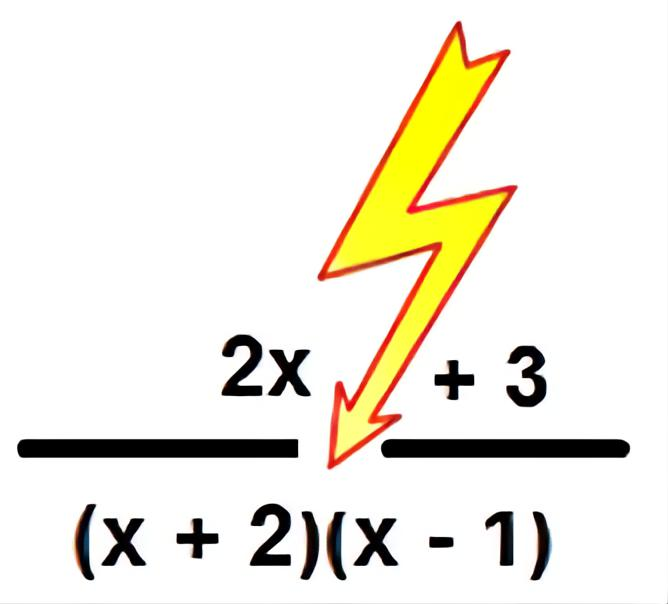 |
|
Hier werden alle wichtigen Ergebnisse und Formeln aus den vorhergehenden Kapiteln übersichtlich zusammengestellt. |
 |

