Quelle: https://nwm2.net-schulbuch.de/index.phpDruckversion vom 26.04.2024 00:47 Uhr
Startseite Qualifikationsphase Stochastik Grundlagen
Grundlagen der Stochastik aus der Sekundarstufe I
Hier werden die Kompetenzen aufgeführt, die im Lehrplan NRW als Voraussetzung aus der Sekundarstufe I benannt sind.
Es wird auf die Seiten in diesem Lehrwerk verwiesen, die diese Kompetenzen fördern.
Die Schülerinnen und Schüler ...
... deuten Alltagssituationen als Zufallsexperimente: Deuten von Wahrscheinlichkeiten
... simulieren Zufallsexperimente: Simulation von Zufallsexperimenten
... verwenden Urnenmodelle zur Beschreibung von Zufallsprozessen: Urnenmodelle
... beschreiben mehrstufige Zufallsexperimente und ermitteln Wahrscheinlichkeiten mithilfe der Pfadregeln: Baumdiagramme
Von den folgenden Aufgaben sollten Sie mindestens die mit einem Stern gekennzeichneten lösen können.
Wenn Sie Hilfe benötigen, so schlagen Sie in der Einführungsphase hier nach.
Grundlegende Kenntnisse mit Hilfe von Aufgaben überprüfen
Die Aufgaben 1 bis 4 können Sie überspringen, wenn sie schon in der Einführungsphase gestellt worden sind.
... zur Aufgabenseite der Einführungsphase
 Aufgabe 1 |
|
|
Ein Laplace-Würfel wird geworfen. Bestimmen Sie die Wahrscheinlichkeit der Ereignisse: a. „Eine durch 3 teilbare Zahl wird gewürfelt.“b. „Eine Zahl unter 4 ist das Ergebnis.“ |
|
| Aufgabe 2 |
|
|
Eine Laplace-Münze wird zweimal geworfen. Berechnen Sie die Wahrscheinlichkeiten der Ereignisse: |
|
| Aufgabe 3 |
|
|
Eine Laplace-Münze wird dreimal geworfen. Berechnen Sie die Wahrscheinlichkeiten der Ereignisse: |
|
| Aufgabe 4 |
|
|
Ein Laplace-Würfel wird zweimal hintereinander geworfen. Berechnen Sie die Wahrscheinlichkeiten folgender Ereignisse: |
|
| Aufgabe 5: Kugeln ziehen |
|
|
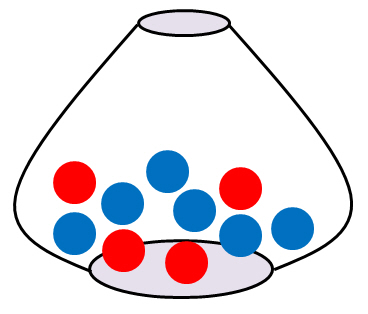
In einem Gefäß liegen vier rote und sechs blaue Kugeln.
|
 |
 Aufgabe 6: Nachkommastelle der Kreiszahl π |
|
|
Sie wählen zufällig eine Ziffer aus den sehr vielen Nachkommastellen der Kreiszahl π.
zu b: Recherchieren Sie im Internet zu den Eigenschaften der Kreiszahl Pi. Von Interesse ist die Frage nach der "Normalität" von Pi: Ist Pi eine "normale Zahl"? Es ist bisher nicht bewiesen, dass die Ziffern in der Dezimaldarstellung der Zahl π gleichverteilt sind, obwohl man das vermutet. Das würde etwa bedeuten, dass die Ziffer 7 unter den ersten zehn Millionen Dezimalen von π ungefähr eine Milliom mal vorkommt. Sie findet sich auch dann tatsächlich 1.000.207-mal, was ziemlich nahe an den erwarteten Wert herankommt. (Quelle: Clifford A. Pickover: Das Mathebuch, 2014 Librero IBP, Kerkdiel, Niederlande, S.320) |
 Foto aus www.spiegel.de im Mathematikum Gießen |
Tipp 1| Aufgabe 7:Messen der Körpergröße |
|
|
Messen der Körpergröße eines zufällig auf einem Schulhof ausgewählten Kindes/Jugendlichen.
Die Anforderungen an ein Zufallsexperiment sind sicher erfüllt. Das Ergebnis jeder Durchführung ist eine reelle Zahl. Die Anzahl der möglichen Zahlen ist von der Messgenauigkeit abhängig. |
 Grafik: kinderfahrradfinder.de |
 Aufgabe 8: Bären in Cornflakes - Packungen |
||||||||||||||||||
|
Vor einigen Jahren warb ein Cornflakes-Hersteller damit, dass sich in jeder seiner Packungen eine kleine Bärenfigur befände. Daraus hat sich die nachfolgende Aufgabe entwickelt. Nehmen Sie an, dass der Hersteller insgesamt vier verschiedene Bären in seinen Packungen hat. Da möchte man natürlich gerne alle Figuren haben. Die Frage ist nun, wie viele Packungen müssen Sie kaufen, bis Sie alle haben.
|
||||||||||||||||||
| Aufgabe 9: "Kieselsteine" |
|
|
Messen des Gewichts eines in einem Haufen gefundenen Kieselsteins
|
 |
| Aufgabe 10: Mittelwert und Median |
|
In der Sekundarstufe 1 haben Sie den Begriff Mittelwert (= arithmetisches Mittel) kennen gelernt. Beantworten Sie die folgenden Fragen:
|
| Aufgabe 11: Wachstum |
|
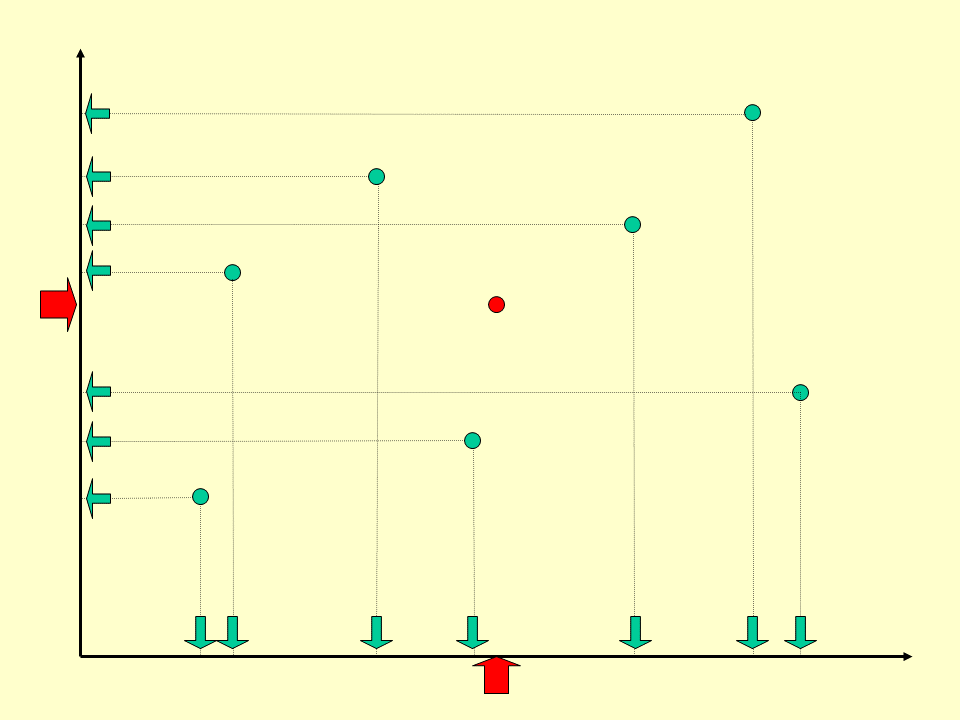
In den abgebildeten Boxplots sind die Daten zur Körpergröße von Mädchen unterschiedlichen Alters (1, 3, 6, 10, 13, 16 Jahre) verarbeitet.
Beschreiben Sie, wie und in welchen Schritten man die nebenstehenden Boxplot-Graphiken aus diesen Daten herstellen kann.
|
| Aufgabe 12: Präsentation |
|
Die Bildfolge zeigt die Folien einer Präsentation. Auf den Folien fehlen die Überschriften. Bearbeiten Sie die folgenden Fragestellungen:
Halten Sie einen Kurzvortrag mit von Ihnen ausgewählten Folien. Dazu können Sie die Präsentation im ODP-Format oder im PPT-Format herunterladen und bearbeiten.
|
