Quelle: https://nwm2.net-schulbuch.de/index.phpDruckversion vom 24.04.2024 15:52 Uhr
Startseite Qualifikationsphase Stochastik Weitere Verteilungen
Weitere Verteilungen
| Hypergeometrische Verteilung
Die hypergeometrische Verteilung ist wie die Binomialverteilung eine diskrete Wahrscheinlichkeitsverteilung. Auch sie verwendet man für Zufallsexperimente mit nur zwei möglichen Ergebnissen. Sie beschreibt aber Zufallsexperimente ohne Zurücklegen im Gegensatz zur Binomialverteilung, die Experimente mit Zurücklegen beschreibt. |
 |
| Geometrische Verteilung
Beim "Mensch-ärgere-dich-nicht" kann man eine Spielfigur erst dann auf den Weg bringen, wenn man eine "6" geworfen hat. Man wartet also auf den sog. ersten Erfolg. Die geometrische Verteilung beschreibt derartige Zufallsversuche. Sie ist eine diskrete Verteilung mit (theoretisch) unendlich vielen Ausfällen. |
 |
| Vollständige Serie
Wie viel Packungen mit Fußballbildern muss man im Mittel kaufen, um eine komplette Serie zu bekommen? Wie groß ist die Wahrscheinlichkeit, in höchstens 20 Würfen alle Augenzahlen eines Würfels zu werfen? Solche und ähnliche Fragen werden in dem Kapitel "Vollständige Serie" beantwortet. |
 |
| Negative Binomialverteilung
Die negative Binomialverteilung (auch Pascal-Verteilung genannt) ist eine Erweiterung der geometrischen Verteilung. Während bei der geometrischen Verteilung der Zufallsversuch solange durchgeführt wird, bis sich ein Erfolg einstellt, wird bei der negativen Binomialverteilung der Versuch solange durchgeführt, bis sich ein Erfolg mehrfach eingestellt hat. |
 |
| Poisson-Verteilung
Die Poisson-Verteilung ist eine gute Annäherung der Binomialverteilung, falls die Wahrscheinlichkeit p klein und die Anzahl der untersuchten Fälle n groß ist. Beispiel: 500.000 Personen werden gegen eine bestimmte Krankheit geimpft. Erfahrungsgemäß treten in 0,1% der Fälle stärkere Nebenwirkungen auf. Wie groß ist die Wahrscheinlichkeit, dass mehr als 1000 Personen derartige Nebenwirkungen bekommen? |
Quelle:en.wikipedia.org |
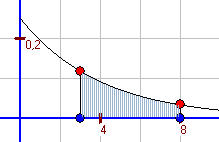
| Exponentialverteilung
Die Exponentialverteilung ist eine stetige Wahrscheinlichkeitsverteilung über der Menge der nicht-negativen reellen Zahlen. Die Dichtefunktion ist eine fallende Exponentialfunktion. Die Wahrscheinlichkeiten werden mithilfe eines Integrals bestimmt. Die Exponentialverteilung wird vorrangig als Modell bei der Frage nach der Länge von Zeitintervallen benutzt, wie z.B.
|
|
