
Quelle: https://nwm2.net-schulbuch.de/index.php
Druckversion vom 27.07.2024 04:45 Uhr
Startseite
Einführungsphase
Funktionen & Analysis
Funktionen
Winkelfunktionen
Winkelfunktionen - Check
 Verständnischeck : alte Bekannte Verständnischeck : alte Bekannte
|
|
Notieren Sie zu den folgenden Aufforderungen kurze Antworten.
- Sie haben in der Sekundarstufe I am rechtwinkligen Dreieck schon den sin(α) und cos(α) kennengelernt. Zeichnen Sie ein beliebiges rechtwinkliges Dreieck mit γ = 90°. Geben Sie an, wie sin(α) und cos(α) berechnet werden.
- Geben Sie an, welche Winkelgrößen α und welche Werte sin(α) in so einem Fall annehmen kann.
- In einem gleichschenkligen Dreieck (b = a) kann man den Wert von sin(α) und cos(α) ohne Kenntnis der Seitenlängen berechnen. Machen Sie sich dazu eine geeignete Skizze und denken Sie an Herrn Pythagoras.
Vergleichen Sie Ihre Aufzeichnungen mit den folgenden Ausführungen.
zu 1.
|
Es gelten die folgenden Definitionen:
`"sin(α)" = \color{green}{"Gegenkathete"}/\color{red}{"Hypotenuse"}`
`"cos(α)" = \color{blue}{"Ankathete"}/\color{red}{"Hypotenuse"}`
|
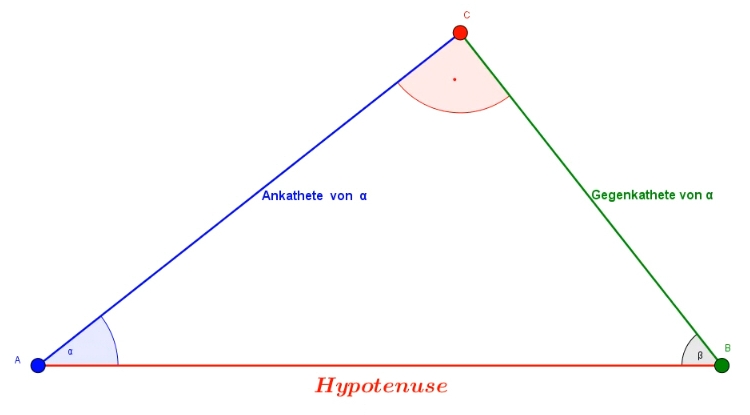 |
| |
|
zu 2.
Da die Winkelsumme 180° ist, können die beiden Basiswinkel zusammen nur 90° groß sein, d.h. 0 < α < 90°. Wegen des Satzes von Pythagoras ist c > a und c > b. Daraus folgt, dass 0 < sin(α) < 1 ist. Eine entsprechende Abschätzung gilt auch für cos(α).
zu 3.
|
Nach Pythagoras gilt:
`a^2 + b^2 = c^2` ⇒ `2a^2 = c^2`
⇒ `a = c/sqrt(2)`
Also ist `sin(α) = a/c = (c/sqrt(2))/c`.
⇒ `sin(α) = 1/sqrt(2) ~~ 0,7071`
Da a = b und α = β ist, folgt für diesen Fall:
`sin(45°) = cos(45°)`
|
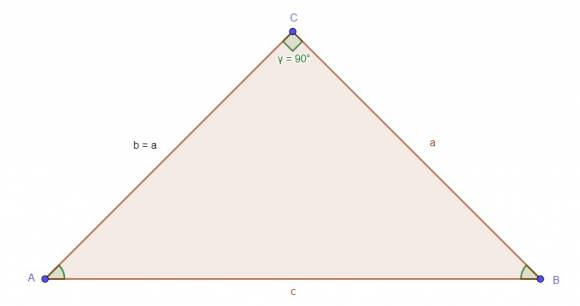 |
|
©2024 NET-SCHULBUCH.DE
 Verständnischeck : alte Bekannte
Verständnischeck : alte Bekannte


