Quelle: https://nwm2.net-schulbuch.de/index.phpDruckversion vom 25.09.2023 17:41 Uhr
Startseite Einführungsphase Analytische Geometrie
Analytische Geometrie
Der Schritt von der Geometrie zur Analytischen Geometrie der Sekundarstufe II ist vor allem ein Wechsel der Betrachtungsweisen und des Vorgehen.
In der Analytischen Geometrie geht es darum, geometrische Sachverhalte rechnerisch zu lösen ohne unbedingt auf eine vorherige Visualisierung zurückzugreifen.
"Jede geometrische Figur kann mit algebraischen Gleichungen beschrieben werden und jede algebraische Gleichung kann als geometrische Figur dargestellt werden."
Diese Aussage wird Renè Descartes (1596-1650) zugeschrieben, der wichtige Grundlagen der Analytischen Geometrie erarbeitet hat.
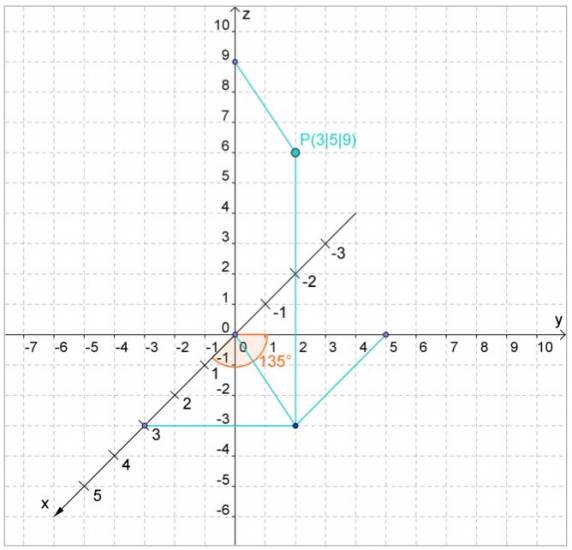
| Koordinaten im Raum Auf diesen Seiten sind der Raum und seine Koordinaten das zentrale Thema.
|  |
| Vektoren Das Ziel ist, geometrische Figuren und Bewegungen im Raum mathematisch zu beschreiben und rechnerisch zu lösen. Dazu wird als neues mathematisches Objekt der Vektor eingeführt. Für Vektoren werden Rechenoperationen festgelegt, die zu den gewünschten rechnerischen Lösungen führen. Neben anderen Anwendungen werden die Eigenschaften von Dreiecken und Vierecken mithilfe von Vektoren analytisch durch Rechnen bestimmt. |  |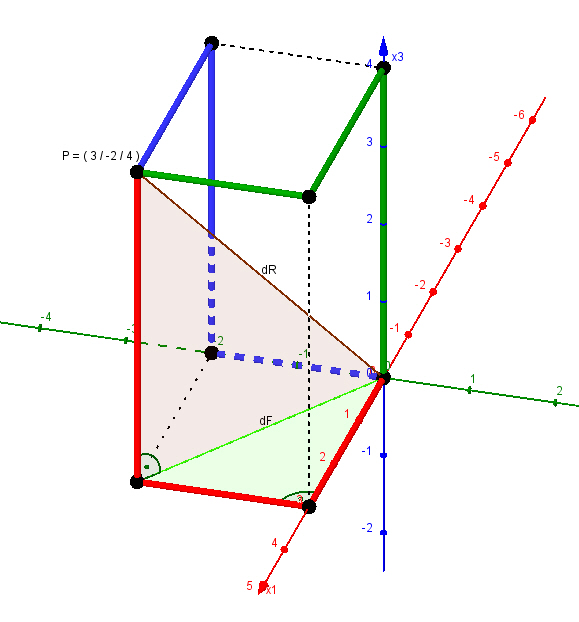
| Geraden Ab dem Schuljahr 2023/24 gehört das Kapitel "Geraden" in NRW zum Lehrplaninhalt in der Einführungsphase.
Daher wird dieses Kapitel noch identisch in der Qualifikationsphase gelistet. (net-code: bc_) | 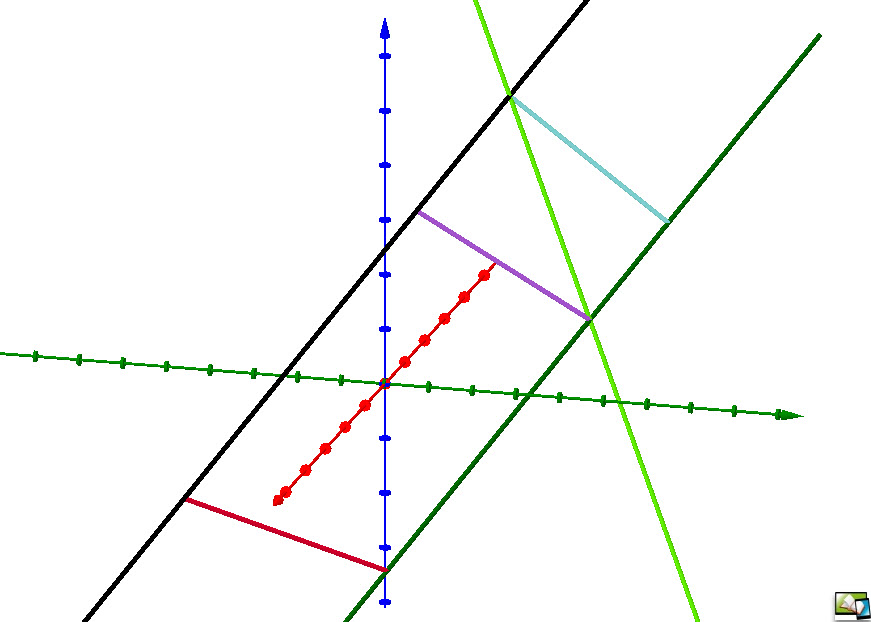 |