Druckversion vom 27.07.2024 08:55 Uhr
Startseite Einführungsphase Funktionen & Analysis Ableitung
Ableitung
test
In diesem Kapitel wird die sogenannte Ableitung aufgegriffen. Dabei handelt es sich um den Grundbegriff der Differentialrechnung, einem Teilgebiet der Analysis und somit der Mathematik.
Das Tangentenproblem.
Gegen Ende des 17. Jahrhunderts entwickelten Gottfried Wilhelm Leibniz und Isaac Newton unabhängig voneinander eine (widerspruchsfrei) funktionierende Technik zum Lösen der Aufgabenstellung.
Der Ausgangspunkt der beiden Wissenschaftler war jedoch unterschiedlich.

Gottfried Wilhelm von Leibniz
Bildnachweis:Wikipedia
Für Leibniz war der Ausgangspunkt eine geometrische Herangehensweise zum lange ungelösten Tangentenproblem.

Sir Isaac Newton
Bildnachweis:Wikipedia
Newton näherte sich dem physikalisch über das Momentangeschwindigkeitsproblem.
Die Ergebnisse beider Forscher erlaubten das Abstrahieren von rein geometrischen oder physikalischen Vorstellungen und werden deshalb als Beginn der Differentialrechnung betrachtet.
Beide Zugänge werden in diesem Lehrwerk betrachtet.
|
Steigung in der Alltagssprache Ziel dieses Kapitels ist das intuitive Erfassen von unterschiedlichen Qualitäten der Steigung eines Funktionsgraphen. Dabei wird auf eine rechnerische Behandlung an dieser Stelle verzichtet. Desweiteren werden die in Alltagsformulierungen vorkommenden Beschreibungen von zeitlichen Prozessen durch diese unterschiedlichen Qualitäten des Steigungsbegriffs genauer charakterisiert. |
Quelle: pixabay.com |
|
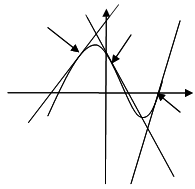
Ausgehend von einem Anwendungsproblem, in dem die Tangente in einem Punkt eines Graphen gesucht wird, wird die Steigung eines Funktionsgraphen in einem Punkt erarbeitet. |
 |
|
Hier wird ein alternativer Zugang zur Herleitung des Ableitungsbegriffs behandelt. Die physikalische Fragestellung von Isaac Newton wird nachvollzogen. "Gefühlt" ist beim Fahren mit einem Fahrrad, Auto, in der Eisenbahn oder für das Fliegen mit einem Flugzeug klar, was Geschwindigkeit ist. Wie aber wird der Wert ermittelt, den die Tachonadel anzeigt? |
 |
|
Die mathematische Berechnung der Ableitung einer Funktion in einem Punkt wird erarbeitet und geübt. |
.jpg) |
|
Ableitungsfunktion - graphisch Aus einem gegebenen Funktionsgraphen wird der Graph abgeleitet, dessen Funktionswerte an jeder Stelle den Wert der Ableitung der Funktion angeben. Das geschieht zunächst durch Zeichnen. Den anschaulichen Hintergrund für die Vorgehensweise liefert die Beobachtung von Altimeter (Höhenmesser) und Variometer im Cockpit eines Segelflugzeuges während des Fluges (Film). Außerdem werden Anwendungsaufgaben aus den Bereichen Geschwindigkeit, Höhenprofile, Bezinverbrauch und Steuertarife angeboten. |
 |
|
Ableitungsfunktion - rechnerisch Die mathematische Berechnung der Ableitungsfunktion einer Funktion wird aus der Berechnung der Ableitung in einem Punkt hergeleitet. |
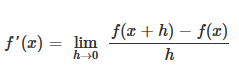 |
|
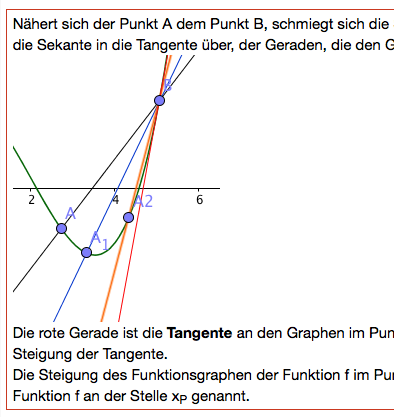
In diesen Kapitel werden noch einmal alle Definitionen und Sätze des Themas zusammengefasst. |
 |


