
Quelle: https://nwm2.net-schulbuch.de/index.php
Druckversion vom 27.07.2024 05:54 Uhr
Startseite
Einführungsphase
Funktionen & Analysis
Funktionen
Winkelfunktionen
Winkelfunktionen - Aufgaben 2
 Aufgabe W1 Aufgabe W1
|
|
Bestimmen Sie alle Winkel zwischen `0 ≤ x ≤ 2pi`, für die gilt:
- `sin(x) = 0`
- `cos(x) = 0`
- `cos(x) = -1`
- `sin(x) = 0.5`
- `sin(x) = 0.31`
- `cos(x) = -0.31`
|
 Aufgabe W2 Aufgabe W2
|
|
Es gibt ein Problem:
Der Taschenrechner gibt an: `cos(200^@) = - 0.9397`.
Anschließend bestimmt man mit `2"nd" cos(-0.9397)` den zugehörigen Winkel und der Taschenrechner gibt `160^@` an.
Helfen Sie!
|
|
 Aufgabe W3 Aufgabe W3
|
|
Berechnen Sie:
|
|
Haben Sie den TR auf R (Bogenmaß) umgestellt? |
|
 Aufgabe W4 - Mondmathematik Aufgabe W4 - Mondmathematik |
|
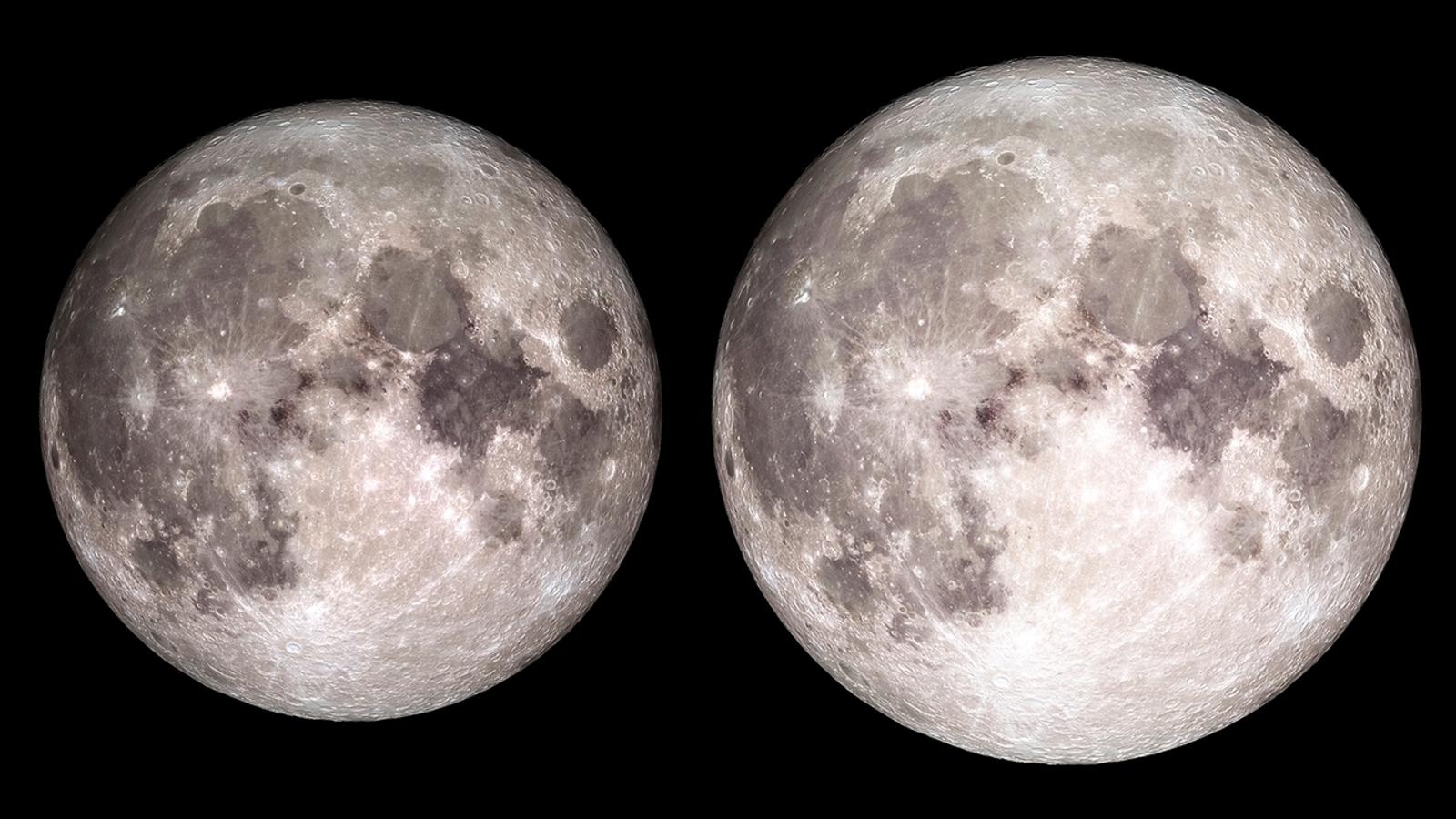
"Am kommenden Wochenende leuchtet der größte Vollmond des Jahres am Himmel. Da sich der Mond auf seiner eiförmigen Bahn gerade in Erdnähe befindet, erscheint er rund 14 Prozent größer und 30 Prozent heller als der kleinste Vollmond 2009. Das teilte die US-Raumfahrtbehörde Nasa mit. Am Samstagmittag ist der Mond der Erde am nächsten und 357 500 Kilometer entfernt. Vollmond ist am Sonntag um 4.27 Uhr."
Westfälische Nachrichten, 10.01.2009
- Erläutern Sie, warum im Artikel ein Ereignis beschrieben wird, das wegen seiner Seltenheit meldenswert ist.
- Korrigieren Sie die "eiförmige Bahn".
- Zur `14 %-`Angabe:
- Die `14 %-`Angabe bezieht sich auf den Monddurchmesser.
Erläuteren Sie, was sie bedeutet.
- Notieren Sie den Zusammenhang zwischen den wahrgenommenen Radien für den erdfernsten (rfern) und erdnächsten (rnah) Punkt.
- Zur `30 %-`Angabe:
- Welche (geometrische) Figur steht hell am Himmel?
- Notieren Sie je eine Formel für den Vollmondkreis mit den beiden Radien aus c.2.
Bringen Sie diese in einer Gleichung zusammen.
- Ermitteln Sie den Faktor zwischen der Kreisfläche, wenn sich der Mond nah (Anah) bei bzw. fern (Afern) von der Erde befindet.
- Zu den Entfernungen:
Info I:
Für kleine Winkel im Bogenmaß gilt `tan(x) ~~ x`. Info II:
Der mittlere Mondabstand beträgt `384 400 km` mit Abweichungen um `5.5 %` nach oben und unten (wikipedia.de).
- Formulieren Sie einen trigonometrischen Zusammenhang zwischen Sehwinkel, Mondentfernung und -radius für die beiden besonderen Punkte (s. c.2., d.3).
- Leiten Sie mit der Information aus den beiden Gleichungen die Entfernung im erdfernsten Punkt her.
- Berechnen Sie mit der neuen Durchmesserabweichung die Abweichung der wahrgenommenen Fläche neu und vergleichen Sie sie mit c.
|
Quelle: https://img.br.de/55b1beba-5650-41c2-be10-2acd6c20af8f.jpeg?rect=0,0,1280,720&w=1600&h=900
|
©2024 NET-SCHULBUCH.DE
 Aufgabe W1
Aufgabe W1 Aufgabe W2
Aufgabe W2 Aufgabe W3
Aufgabe W3

 Wenn`s hakt!
Wenn`s hakt!