Quelle: https://nwm2.net-schulbuch.de/index.phpDruckversion vom 24.03.2023 05:09 Uhr
Startseite Einführungsphase Funktionen & Analysis Funktionen
Funktionen
Eine Funktion wird im Normalfall mit einer Funktionsgleichung der Form `f(x) = y = ...` angegeben. Diese Funktionsgleichungen können in verschiedene Klassen aufgeteilt werden, z.B. in Potenzfunktionen oder Exponentialfunktionen. Diese Klassen werden in den folgenden Abschnitten untersucht.
Wiederholend werden die wichtigen Eigenschaften von linearen und quadratischen Funktionen aus der Sekundarstufe I behandelt.
Außerdem finden Sie hier eine Zusammenstellung der gebräuchlichsten Symbole und Schreibweisen zur Darstellung von Funktionen.
y = f(x) = m·x + n
y = g(x) = a·x² + b·x + c
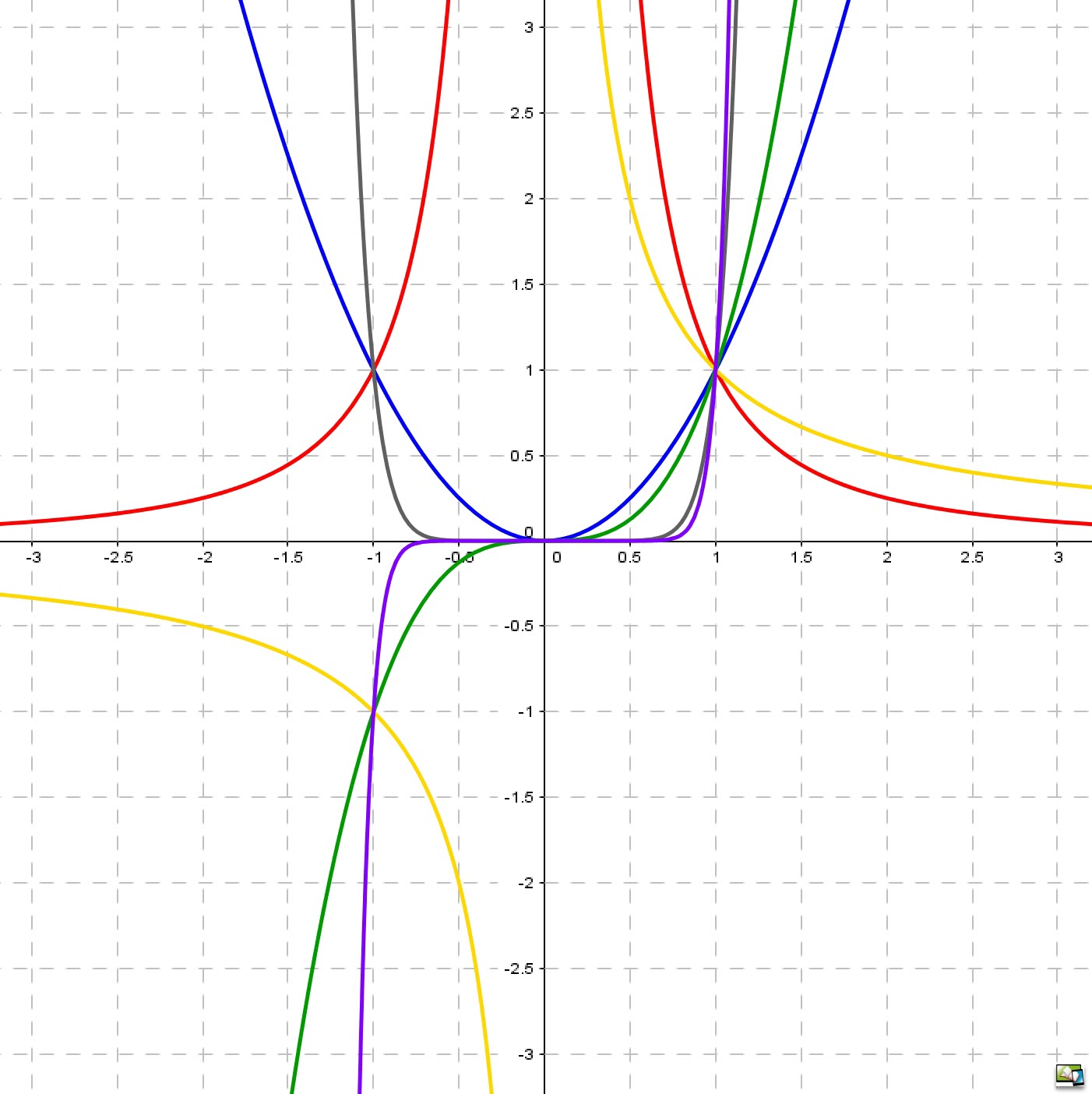
Grundlegende Eigenschaften der Funktionen f mit f(x) = `x^n` (`n in ZZ`) und ihrer Graphen werden erforscht, analysiert und erläutert.
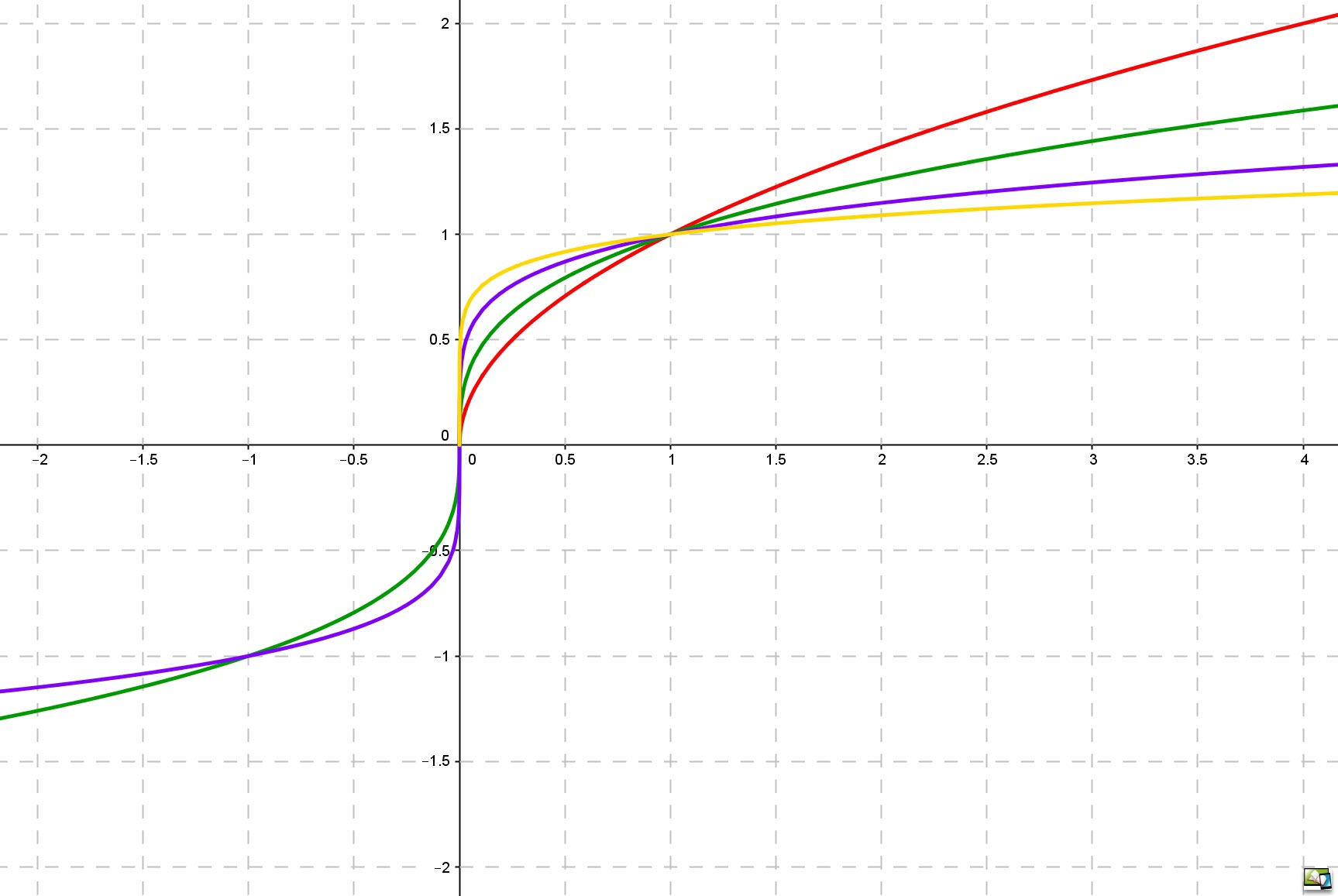
Wurzelfunktionen f mit f(x) = `x^(1/n)`= `root n (x)` (`n in NN`, n`>= 2`) werden als Umkehrfunktionen spezieller Potenzfunktionen erforscht, analysiert und graphisch dargestellt.
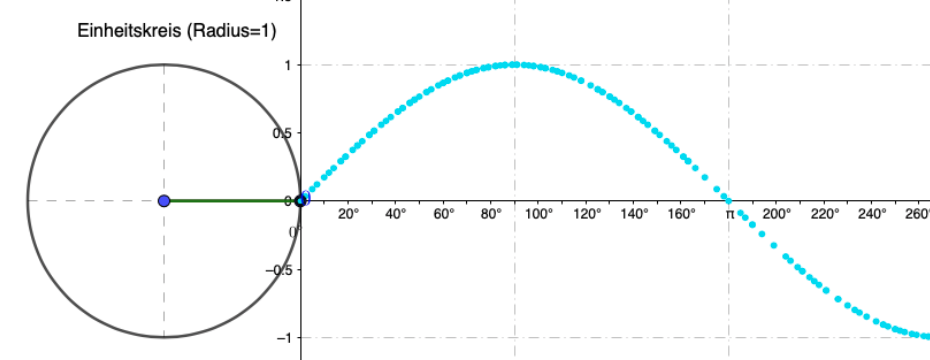
Wiederholend werden die Winkelfunktionen - mit dem Schwerpunkt auf der Sinus-Funktion - ausgehend von der Definition am rechtwinkligen Dreieck untersucht und ihre Graphen auf der Grundlage des Bogenmaßes erforscht.
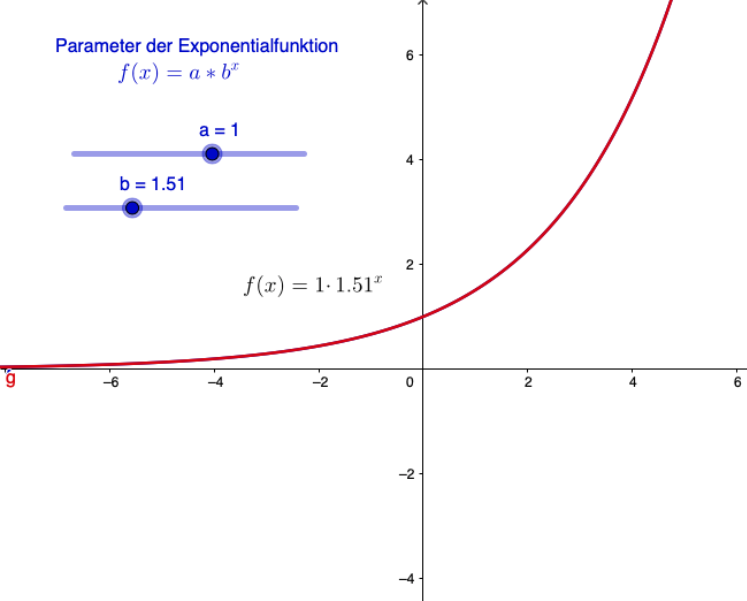
Exponentielle Wachstums- und Zerfallsprozesse stehen im Zentrum der Anwendung der Exponentialfunktionen, deren Graphen und Verläufe ausführlich untersucht werden.
Polynome / Ganzrationale Funktionen
Ganzrationale Funktionen und Polynome spielen eine zentrale Rolle bei der beispielhaften Untersuchung und mathematischen Modellierung von Alltagssituationen und Beziehungen mit Hilfe von Funktionen.Die Untersuchung dieser Funktionsklasse mit analytischen Verfahren steht im Mittelpunkt.
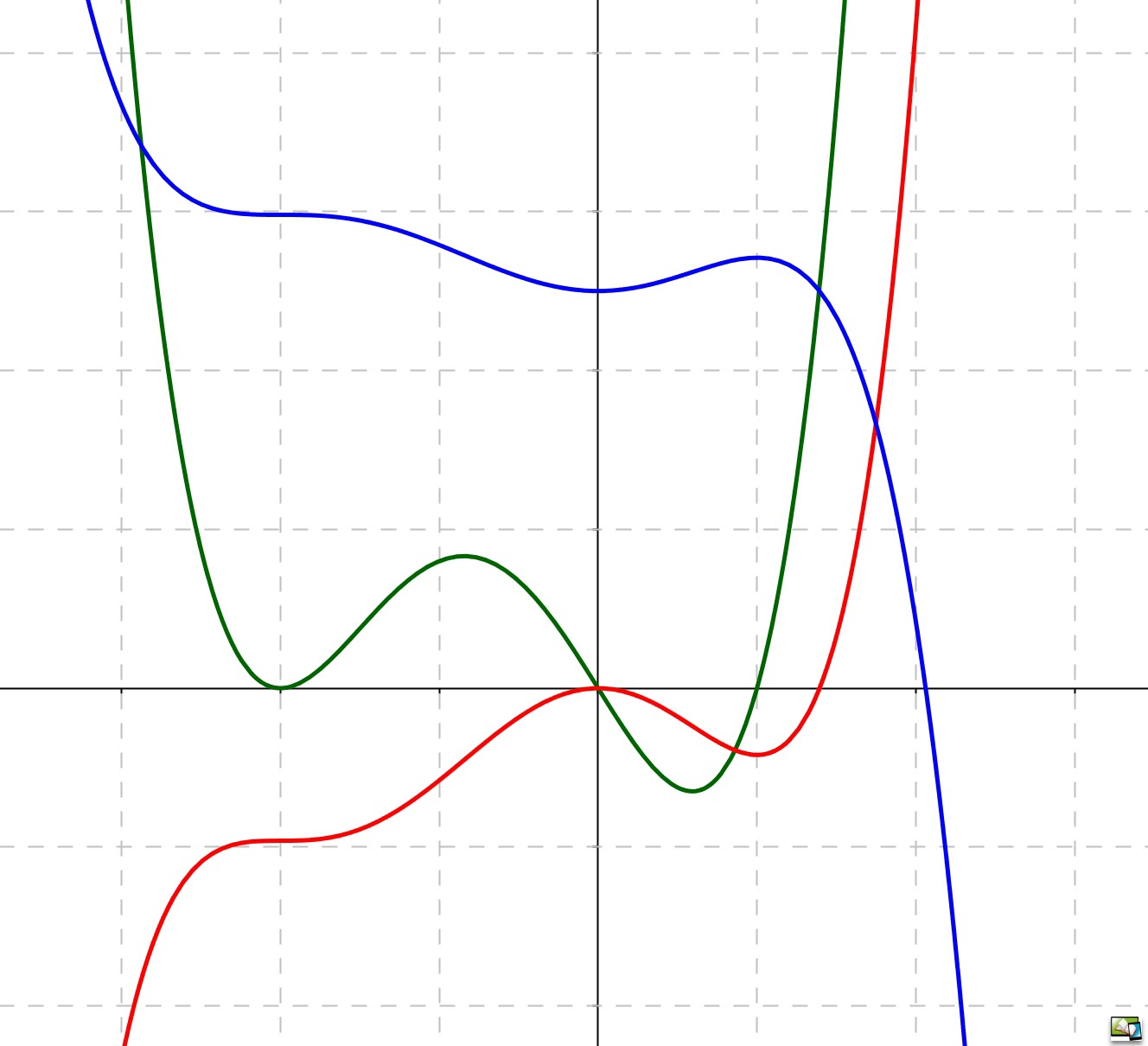
Die Transformation von Funktionen und die Auswirkungen auf ihre Graphen werden allgemein analysiert und anhand der verschiedenen Funktionsklassen erläutert.
Es werden Verschiebungen, Spiegelungen, Stauchungen und Streckungen anhand der vorkommenden Funktionsklassen untersucht.
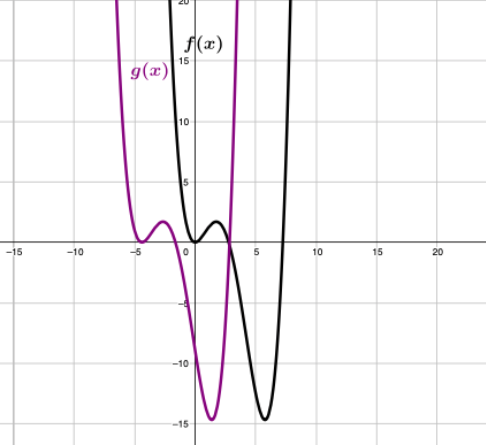
Alle behandelten zentralen Eigenschaften und Sätze werden zusammenfassend aufgeführt und dadurch weitere Studien in der Qualifikationsphase vorbereitet.
