Druckversion vom 16.05.2024 01:06 Uhr
Startseite Einführungsphase Stochastik Bed. Wahrscheinlichkeit Bayes-Wahrscheinlichkeit
Bedingte Wahrscheinlichkeiten & der Satz von Bayes - Lehrtext
Man berechnet demnach den Anteil der Fälle beim Eintreten eines Ereignisses B, in denen auch das Ereignis A eintritt.
Sprechweise: "Die Wahrscheinlichkeit von B unter der Bedingung A"
Beispiel: Wenn Sie aus einer Urne mit 3 schwarzen und 2 roten Kugeln zweimal ohne Zurücklegen ziehen, dann gilt für den zweiten Zug:
- Die Wahrscheinlichkeit, dass man eine schwarze Kugel zieht, wenn man im ersten Zug eine rote gezogen hat, `P("schwarz"|"rot") = 3 / 4 = 0,75`.
- Die Wahrscheinlichkeit, dass man eine schwarze Kugel zieht, wenn man im ersten Zug eine schwarze gezogen hat, `P("schwarz"|"schwarz") = 2 / 4 = 0,5`.
Beispiel:
P (krank und positives Testergebnis): Die Wahrscheinlichkeit, dass eine Person krank ist und ein positives Testergebnis hat.
P (krank | positives Testergebnis): Die Wahrscheinlichkeit, dass eine Person krank ist unter der Bedingung, dass ihr Test (bereits) positiv ausgefallen ist.
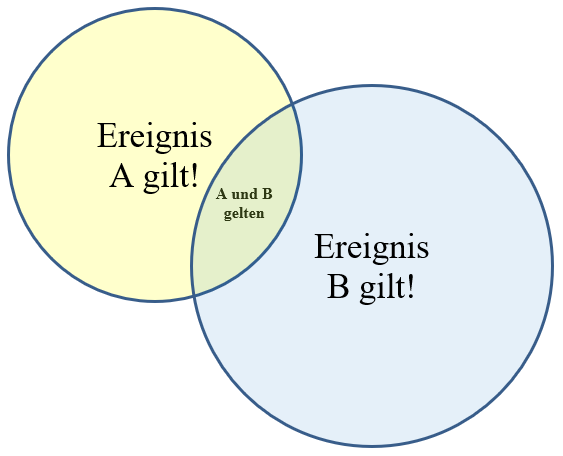
`P(A | B) = (P(A" und "B))/(P(B)) = "A und B gelten" / "Ereignis B gilt" = "gelb-blaue Fläche" / "blaue Fläche" `
Das nebenstehende Baumdiagramm zeigt, dass sich die nachfolgende Formel aus dem obersten Pfad ergibt. Für den gilt: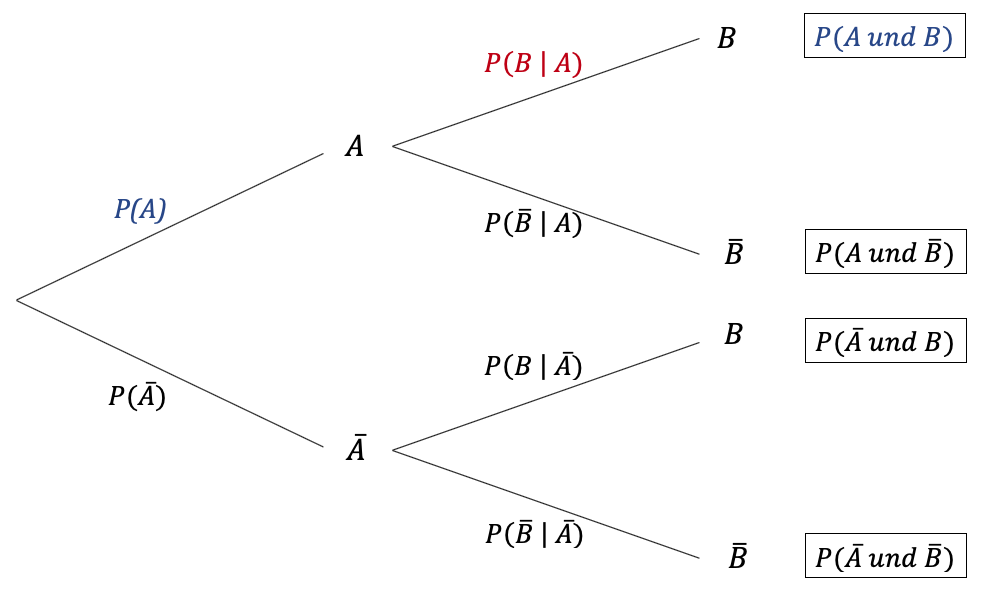
P(A) · P(B | A) = P(A und B).
Durch Umformung erhält man die nachfolgende Berechnungsformel für die bedingte Wahrscheinlichkeit P(B | A):
` P(B | A) = (P(A " und " B))/(P(A)) `
Statt eines Baumdiagramms kann auch eine Vierfeldertafel zur Berechnung der bedingten Wahrscheinlichkeiten aufgestellt werden. Hier stehen die Pfadwahrscheinlichkeiten in den inneren Feldern, die einfachen Wahrscheinlichkeiten auf den Summenrändern. Somit kann man die obige Formel direkt anwenden (siehe dunkelblaue Felder):
| Vierfeldertafel | `A ` | `bar A ` | Summen |
| `B ` |
`P(A " und " B) ` |
`P(bar A " und " B) ` |
`P(B)` |
| `bar B ` |
`P(A " und " bar B) ` |
`P(bar A " und " bar B) ` |
`P(bar B)` |
| Summen | `P(A)` | `P(bar A)` | Gesamt-Summe |
In beiden Fällen gilt: `P(B | A) = (n(A " und " B))/(n(A)) = (n(A " und " B))/(n(A " und " B) + n(A " und " barB))`
⇒` ((n(A " und " B))/n)/((n(A))/n) = (P(A " und " B))/(P(A)) = P(B |A)`
Im Baumdiagramm schreibt man die Anzahl der Fälle, die zu einem Ereignis gehören, am besten an den entsprechenden Knotenpunkt:
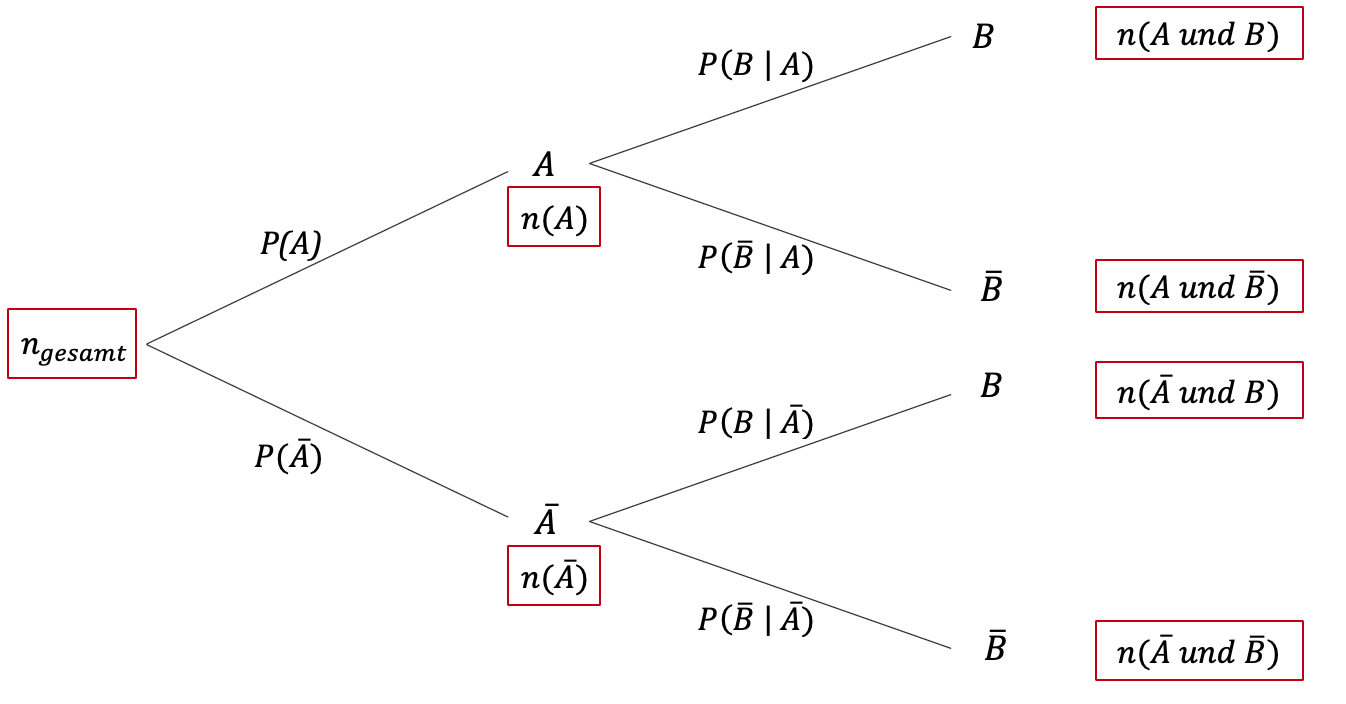
In die Vierfeldertafel werden die absoluten Häufigkeiten eingetragen:
| Vierfeldertafel | `A` | `barA` | Summen |
| `B ` | `n(A " und " B)` | `n(barA " und " B)` | `n(B)` |
| `barB` | `n(A " und " barB)` | `n(barA " und " barB)` | `n(barB)` |
| Summen | `n(A)` | `n(barA)` | Gesamtsumme |
Beim umgekehrten Baumdiagramm stehen `B` und `barB` an den ersten Knotenpunkten. Die dafür nötigen Wahrscheinlichkeiten können Sie aus der Vierfeldertafel oder auch aus dem Baumdiagramm zu Fall I übernehmen. Bitte beachten Sie, dass `P(A " und " B) = P(B " und " A)` usw. gilt.
Analog zur obigen Berechnungsformel gilt dann: 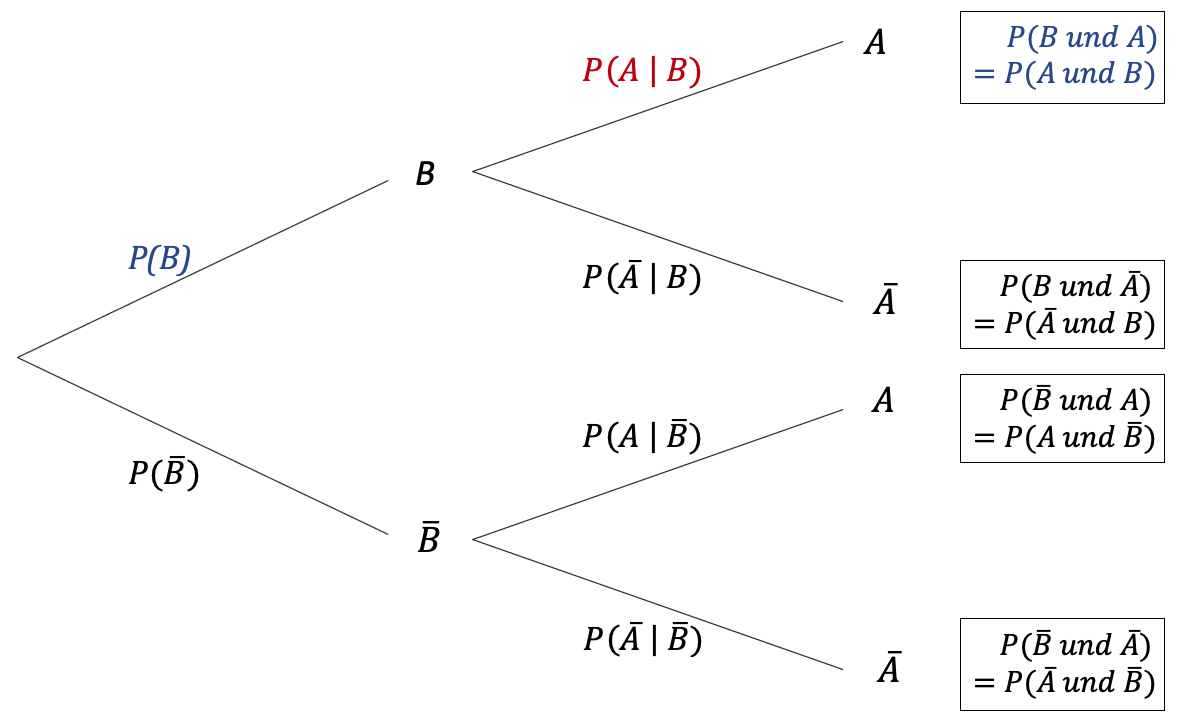
`P(A | B)` = `(P(B " und " A))/(P(B))` = `(P(A " und " B))/(P(B))`.
| Vierfeldertafel | `A ` | `bar A ` | Summen |
| `B ` |
`P(A " und " B) ` |
`P(bar A " und " B) ` |
`P(B)` |
| `bar B ` |
`P(A " und " bar B) ` |
`P(bar A " und " bar B) ` |
`P(bar B)` |
| Summen | `P(A)` | `P(bar A)` | Gesamt-Summe |
In beiden Fällen gilt: `P(A | B) = (n(A " und " B))/(n(B)) = (n(A " und " B))/(n(A " und " B) + n(barA " und " B))`
Im Baumdiagramm schreibt man die Anzahl der Fälle, die zu einem Ereignis gehören, am besten an den entsprechenden Knotenpunkt:
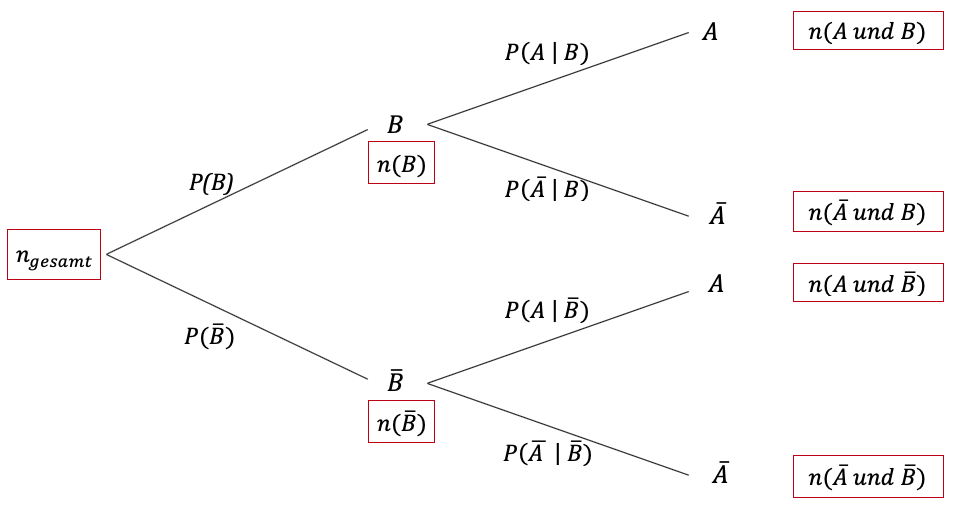
In die Vierfeldertafel werden die absoluten Häufigkeiten eingetragen:
| Vierfeldertafel | `A` | `barA` | Summen |
| `B ` | `n(A " und " B)` | `n(barA " und " B)` | `n(B)` |
| `barB` | `n(A " und " barB)` | `n(barA " und " barB)` | `n(barB)` |
| Summen | `n(A)` | `n(barA)` | Gesamtsumme |
Sie können auch mit dem Baumdiagramm aus Fall I weiterarbeiten, wenn Sie die beiden folgenden Sätze kennen.
Dann gilt: `P(B) = P(A " und " B) + P(barA " und " B)`
Anschaulich: Wenn `A " und " barA` an den ersten Knotenpunkten in einem zweistufigen Baumdiagramm stehen, dann berechnen Sie `P(B)`, indem Sie die Wahrscheinlichkeiten aller Pfade addieren, die zu `B` führen.
Dann gilt:
`P(A|B) = (P(A)*P(B|A))/(P(B))=(P(A " und " B))/(P(A " und " B) + P(barA " und " B))`
Anschaulich: Dividieren Sie die Pfadwahrscheinlichkeit `P(A " und " B)` durch die Summe der Wahrscheinlichkeiten aller Pfade, die zu `B` führen.
Die verschiedenen Ansätze sind im Beispiel Diabetestest ausführlich beschrieben!
Diabetes-Test
Blutspenden werden auf Diabetes untersucht, der mit 8% in der Bevölkerung verbreitet ist. Dabei werden an Diabetes Erkrankte mit einer Wahrscheinlichkeit von 95% erkannt, während 2% als Diabetiker eingestuft werden, obwohl sie es nicht sind.
- Berechnen Sie die Wahrscheinlichkeit dafür, dass das Testergebnis „kein Diabetiker“ lautet.
- Berechnen Sie die Wahrscheinlichkeit dafür, dass ein als Diabetiker eingestufter Spender (Test positiv) tatsächlich an Diabetes erkrankt ist.
Welchen Lösungsweg möchten Sie gehen, wenn Sie bedingte Wahrscheinlichkeiten bei Aufgabenteil b berechnen wollen? Mithilfe eines umgekehrten Baumdiagramms, einer Vierfeldertafel oder direkt mit dem Satz von Bayes? Verschiedene Lösungswege sind möglich, aber nicht alle gleich schnell ...
Vergleichen Sie die unten aufgeführten Beispiele, wie man bei der Diabetes-Aufgabe zum Aufgabenteil b vorgehen kann.
Schritt für Schritt zur Lösung
I. Schritt
Aufstellen eines Baumdiagramms mit den Werten aus dem Aufgabentext
Diabetes-Test
Blutspenden werden auf Diabetes untersucht, der mit 8% in der Bevölkerung verbreitet ist. Dabei werden an Diabetes Erkrankte mit einer Wahrscheinlichkeit von 95% erkannt, während 2% als Diabetiker eingestuft werden, obwohl sie es nicht sind.
1. Textpassage
„der mit 8% in der Bevölkerung verbreitet ist.“
Prävalenz `hat =` „der mit 8% in der Bevölkerung verbreitet ist.“ `hat =` P(D+)
2. Textpassage
"werden an Diabetes Erkrankte mit einer Wahrscheinlichkeit von 95% erkannt"
eine Bedingung `hat =` an Diabetes Erkrankte `hat =` D+
werden … erkannt `hat =` T+
mit einer Wahrscheinlichkeit von 95% `hat =` P( __ | __ ) = 0,95
`rArr` `P( T+ | D+) = 0,95` `hat =` "Wahrscheinlichkeit für einen positiven Test, wenn man an Diabetes erkrankt ist."
3. Textpassage
"2% als Diabetiker eingestuft werden, obwohl sie es nicht sind."
eine Bedingung `hat =` obwohl sie es nicht sind `hat =` D-
als Diabetiker eingestuft werden `hat =` T+
2% `hat =` P( __ | __ ) = 0,02
`rArr` `P(T+|D-) = 0,02 ` `hat =` "Wahrscheinlichkeit für einen positiven Test, wenn man nicht an Diabetes erkrankt ist"
Am Ende können Sie die Wahrscheinlichkeiten aus dem Aufgabentext bereits in ein Baumdiagramm (oder eine Vierfeldertafel) eintragen.
|
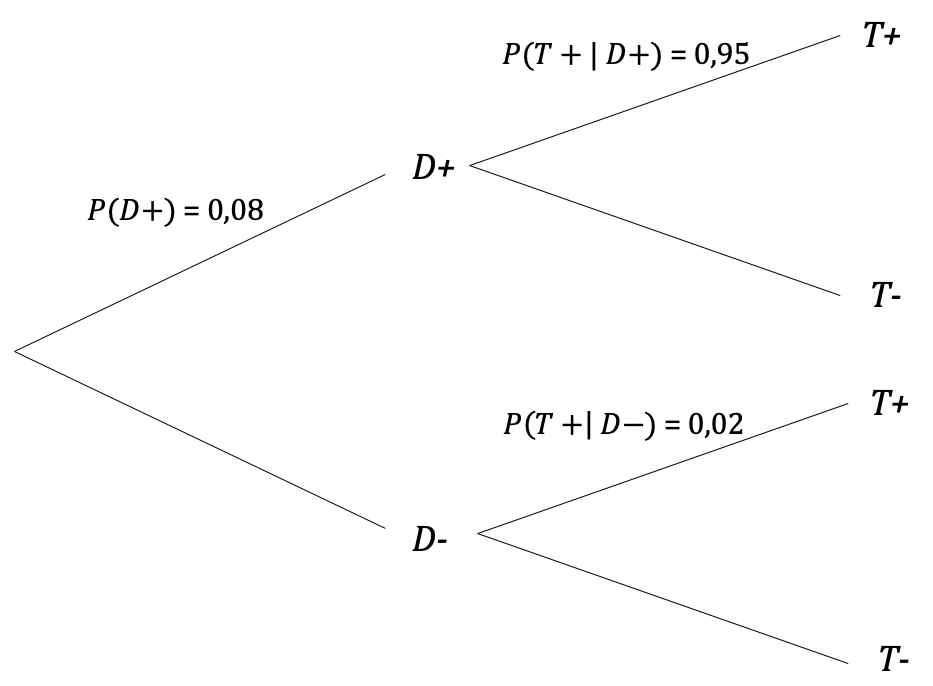
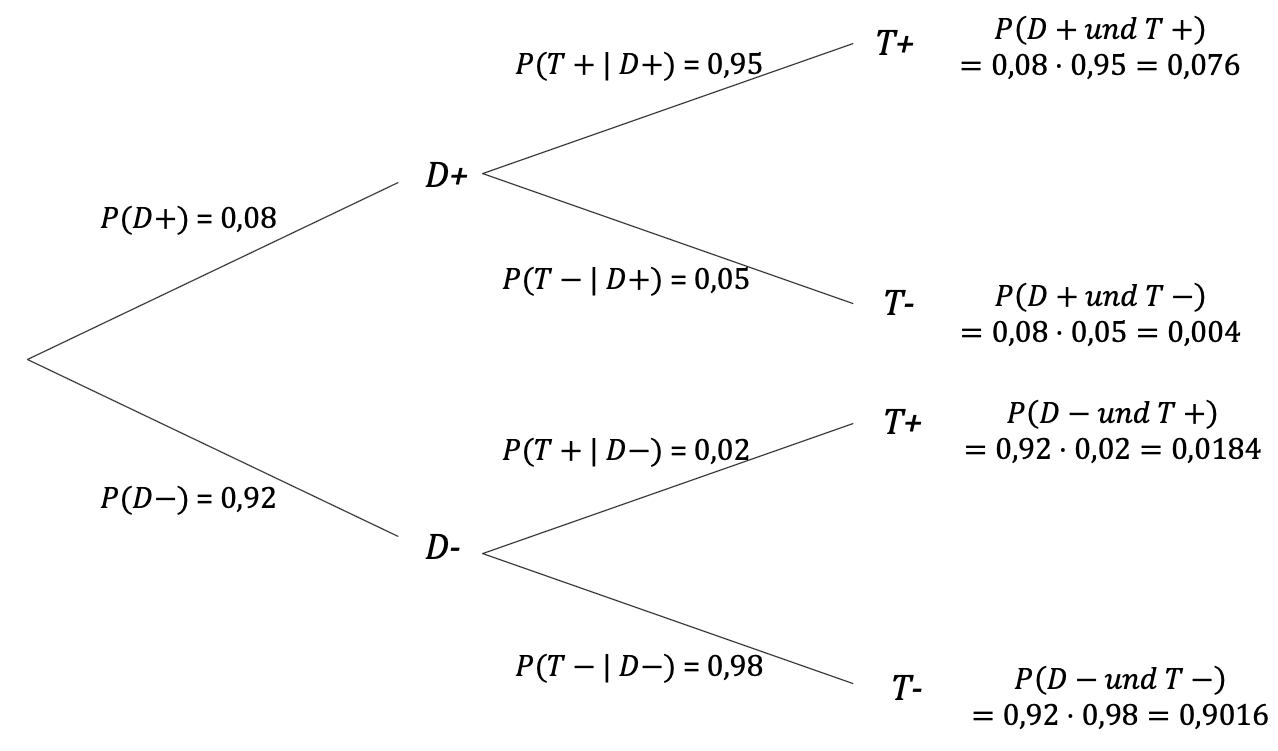
1. Einführung von Bezeichnungen und Übertragung der gegebenen Daten in ein Baumdiagramm D+: Eine Person ist an Diabetes erkrankt, also `P(D+) = 0,08 ` D-: Eine Person ist nicht an Diabetes erkrankt, also `P(D-) = 0,92 ` T+: Der Test fällt positiv aus. T-: Der Test fällt negativ aus. Beachten Sie, dass die Wahrscheinlichkeiten für T+ und T- nicht gegeben sind. Vielmehr sind bedingte Wahrscheinlichkeiten gegeben: Des Weiteren ist die bedingte Wahrscheinlichkeit gegeben `P(T+|D-) = 0,02 `. |
Mit diesen Daten und Bezeichnungen ergibt sich das Baumdiagramm:
|
2.
Vervollständigung des Baumdiagramms
Es können sofort die Gegenwahrscheinlichkeiten `P(D-) = 0,92`, `P(T-|D+) = 0,05` und `P(T-|D-) = 0,98 ` eingetragen werden. Nach der Pfadregel ergeben sich auch die Wahrscheinlichkeiten an den Pfadenden:
`P(D+ "und" T+) = 0,08⋅0,95 = 0,076`
[gelesen: Wahrscheinlichkeit für Diabetes und positiver Test]
`P(D+ "und" T-) = 0,08⋅0,05 = 0,004`
`P(D- "und" T+) = 0,92⋅0,02 = 0,0184`
`P(D- "und" T-) = 0,92⋅0,98 = 0,9016`
Somit hat man das vollständige Baumdiagramm:
II. Schritt
Variante a: Bearbeiten der Aufgabe - mit einem Baumdiagramm
zu a. Berechnen Sie die Wahrscheinlichkeit dafür, dass das Testergebnis „kein Diabetiker“ lautet.
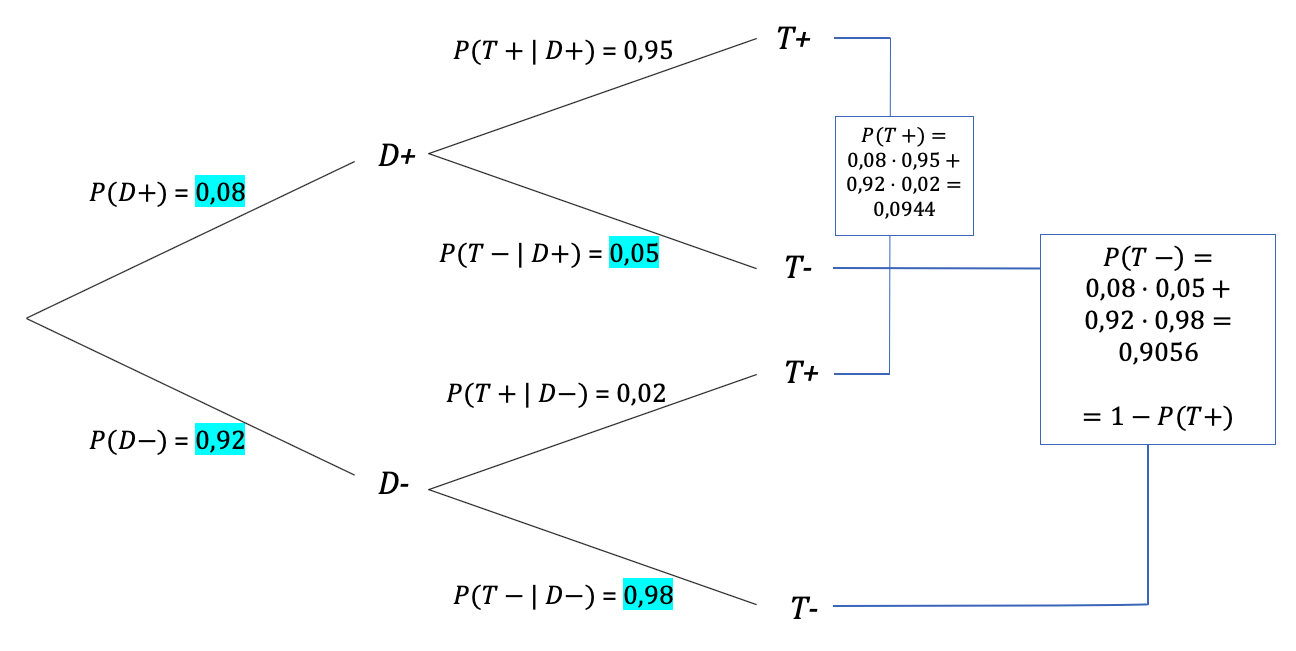
Die Frage, mit welcher Wahrscheinlichkeit das Testergebnis „kein Diabetiker“ lautet, kann nun beantwortet werden. Es ist also `P(T-)` zu bestimmen. Nach dem Satz von der totalen Wahrscheinlichkeit ist dies die Summe der Wahrscheinlichkeiten der beiden Pfade, die zu dem Ereignis T- gehören:
`P(T-) = P(D+ "und" T- ) + P(D- "und" T-) = 0,004 + 0,9016 = 0,9056`.
Also erhalten 90,56% der Getesteten ein negatives Testergebnis.
zu b. Berechnen Sie die Wahrscheinlichkeit dafür, dass ein als Diabetiker eingestufter Spender (Test positiv) tatsächlich an Diabetes erkrankt ist.
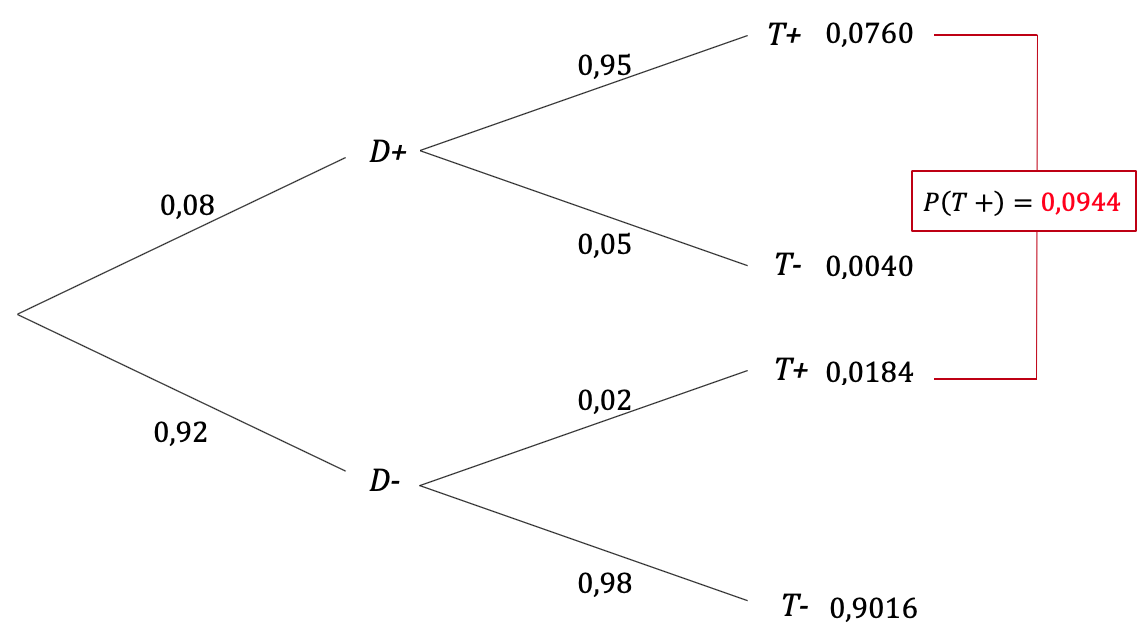
Das ist die Frage nach dem positiven Vorhersagewert `P(D+|T+)`, den Sie nicht direkt aus dem obigen Baumdiagramm ablesen können. Addieren Sie allerdings die Pfadwahrscheinlichkeiten der Pfade, die zu T+ führen, so erhalten Sie `P(T+)` und damit auch `P(T-) = 1 - P(T+)`.
Damit können Sie das umgekehrt Baumdiagramm aufstellen, weil die Pfadwahrscheinlichkeiten gleich bleiben.
| Baumdiagramm | umgekehrtes Baumdiagramm |
 |
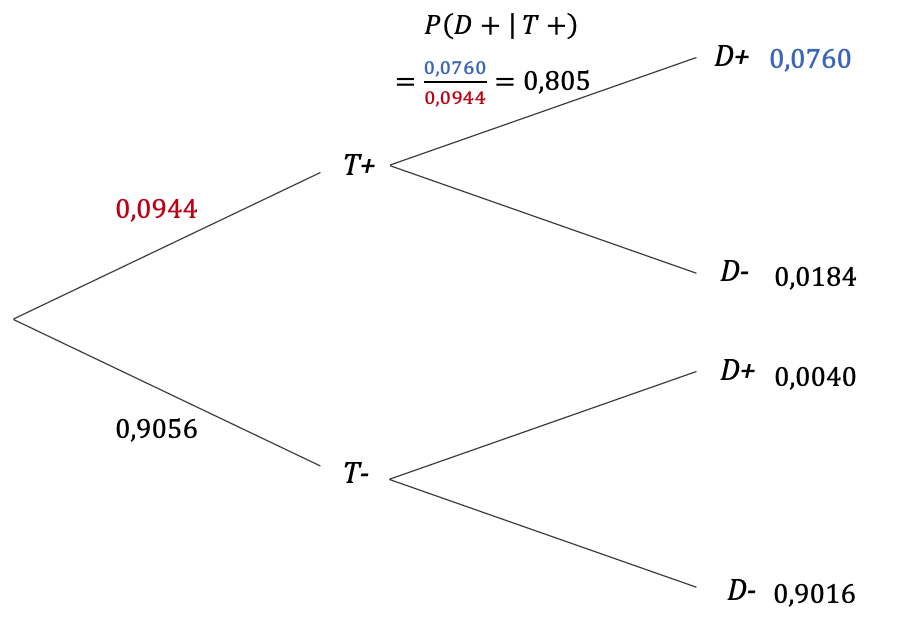 |
Die Wahrscheinlichkeit, dass der positiv Getestete tatsächlich an Diabetes erkrankt ist, liegt also "nur" knapp über 80%.
Das ist die Frage nach dem positiven Vorhersagewert `P(D+|T+)`, den Sie mithilfe des Satzes von Bayes direkt berechnen können. Es gilt:
`P(D+|T+) = (P(D+)*P(T+|D+))/(P(D+)*P(T+|D+)+P(D-)*P(T+|D-)) `
Am Baumdiagramm können die benötigten Werte abgelesen bzw. bestimmt werden:
`P(D+) = 0,08` und `P(D-) = 0,92`
`P(T+|D+) = 0,95` und `P(T+|D-) = 0,02`
Dann gilt nach dem Satz von Bayes:
`P(D+|T+) = (0,08*0,95)/(0,08*0,95 + 0,92*0,02) = 95/118 ~~ 0,805 = 80,5%`
Die Wahrscheinlichkeit, dass der positiv Getestete tatsächlich an Diabetes erkrankt ist, liegt also "nur" knapp über 80%.
Analog berechnen Sie auch den negativen Vorhersagewert `P(D-|T-)`.
`P(D-|T-) = (0,92*0,98)/(0,92*0,98 + 0,08*0,05) = 1127/1132 ~~ 0,996 = 99,6%`
Die ‚Negativ-Aussage‘ des Test ("Sie haben keine Diabetes-Erkrankung.") ist also sehr sicher.
Variante b: Bearbeiten der Aufgabe - mit einer Vierfeldertafel:
zu a. Berechnen Sie die Wahrscheinlichkeit dafür, dass das Testergebnis „kein Diabetiker“ lautet.
0,076 0,004 0,0184 0,9016 In den inneren vier Feldern stehen die Pfadwahrscheinlichkeiten, z.B. `P(D+ "und " T+) = 0,076` (siehe Baumdiagramme) . Die Randwahrscheinlichkeiten ergeben sich durch Aufsummierung.
Vierfeldertafel
T+
T-
Summen
D+
0,08
D-
0,92
Summen
0,0944
0,9056
1
zu b. Berechnen Sie die Wahrscheinlichkeit dafür, dass ein als Diabetiker eingestufter Spender (Test positiv) tatsächlich an Diabetes erkrankt ist.
Die zweite Frage, mit welcher Wahrscheinlichkeit ein als Diabetiker Eingestufter (Test positiv) tatsächlich an Diabetes erkrankt ist, schreibt sich formal `P(D+|T+)`. Dabei handelt es sich um den positiven Vorhersagewert. Die gesuchte Wahrscheinlichkeit `P(D+|T+)` ist nicht direkt aus der Vierfeldertafel ablesbar. Sie ergibt sich aber durch folgende Rechnung: `P(D+|T+) = (P(T+ " und " D+))/(P(T+))=(0,076)/(0,0944)≈0,805` Begründung: Es handelt sich um den Anteil der Personen, die an Diabetes erkrankt sind und positiv getestet wurden bezogen auf die Gesamtheit der positiv Getesteten.
Variante c: Bearbeiten der Aufgabe - mit absoluten Häufigkeiten:
zu a. Berechnen Sie die Wahrscheinlichkeit dafür, dass das Testergebnis „kein Diabetiker“ lautet.
7600 ` 400 1840 90160
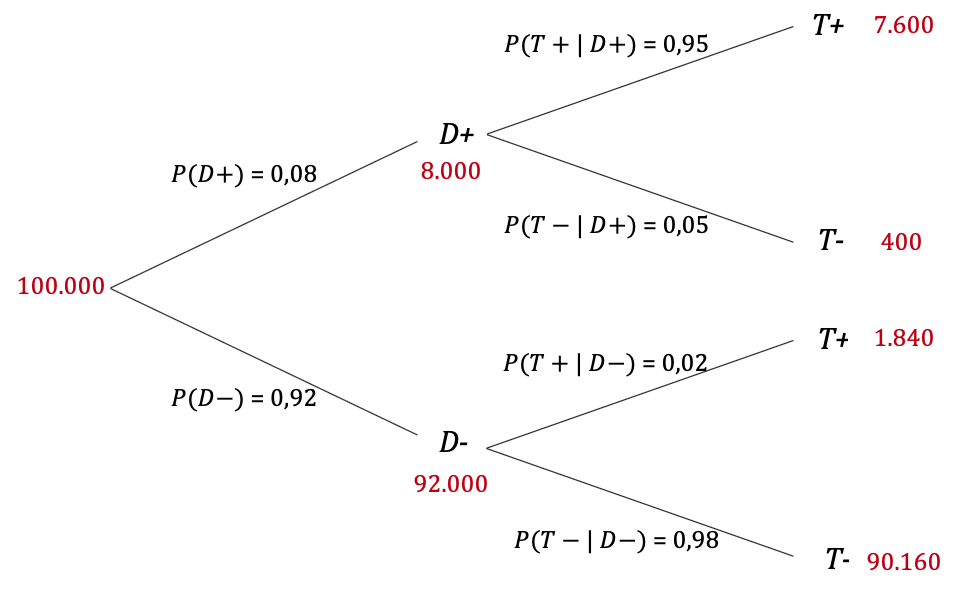
Vierfeldertafel
T+
T-
Summen
D+
8000
D-
92000
Summen
9440
90560
100000
Von 100000 Personen sind 8%, also 8000 an Diabetes erkrankt und folglich 92000 nicht erkrankt. Ein negatives Testergebnis erhalten 5% von den 8000 Erkrankten, also 400 Personen, sowie 98% der Nichterkrankten, also 90160 Personen. Das ergibt 400 + 90160 = 90560 Personen. 90560 von 100000 Personen erhalten also ein negatives Testergebnis: `P(T+) = 90,56%`.
zu b. Berechnen Sie die Wahrscheinlichkeit dafür, dass ein als Diabetiker eingestufter Spender (Test positiv) tatsächlich an Diabetes erkrankt ist.
Ein positives Testergebnis erhalten 95% von den 8000 Erkrankten, also 7600 Personen, sowie 2% der Nichterkrankten, also 1840 Personen. Das ergibt 7600 + 1840 = 9440 Personen. Mit den absoluten Zahlen sollten Sie die Lösung finden, da es sich letztlich um die bekannte Bestimmung mit der Laplace-Regel handelt: "Zahl der günstigen Fälle durch Zahl der möglichen Fälle." "Günstig" meint hier, dass 7600 tatsächlich Erkrankte zu erwarten sind, "möglich" sind alle, die ein positives Testergebnis erhalten werden, also 9440. Die Division ergibt das gesuchte Ergebnis: `P(D+|T+) = 7600/9440 ≈ 80,5 %`.
Dieses Ergebnis für positiven Vorhersagewert sollte Sie überraschen, da der Test zunächst wegen der Richtigdiagnosen mit 95 % bzw. 98 % sehr sicher aussieht. Die Wahrscheinlichkeit an Diabetes erkrankt zu sein, beträgt bei diesen Vorgaben nur ca. 80%, wenn der Test positiv ausgefallen ist! Also zu fast 20% würde er ein falsches Ergebnis liefern. Das gilt natürlich nur für Getestete, für die keine weiteren Informationen bekannt sind. Das ist z.B. ein Grund dafür, keine flächendeckenden Tests bei der Gesamtbevölkerung durchführen zu lassen.
Da bedingte Wahrscheinlichkeiten bei diagnostischen Tests eine besonders große Rolle spielen, sind im Folgenden die dort verwendeten Begriffe erläutert:
Wahrscheinlichkeitsbegriffe für einen diagnostischen Test einer Krankheit
Prävalenz/ Prävalenzrate : absolute oder relative Häufigkeit dieser Krankheit in der betrachteten Gruppe
K+ / K- : Die Krankheit ist vorhanden / nicht vorhanden
T+ / T- : Der Test fällt positiv (er zeigt die Krankheit an) / negativ (er zeigt die Krankheit nicht an) aus.
Gütekriterien eines Tests:
Diese Werte werden in Studien an erkrankten bzw. nichterkrankten Personen ermittelt.
Sensitivität = P(T+ | K+) : Die Sensitivität eines Tests ist die Wahrscheinlichkeit dafür, dass der Test bei einem Erkrankten ein positives Ergebnis anzeigt. " Der Test ist sensibel für diese Krankheit."
Spezifität = P(T- | K-) : Die Spezifität eines Tests gibt die Wahrscheinlichkeit dafür an, dass der Test bei einem Nichterkrankten ein negatives Testergebnis anzeigt. "Der Test reagiert nur speziell auf diese Krankheit."
Für die getesteten Personen sind normalerweise zwei andere Wahrscheinlichkeiten wichtiger:
positiver Vorhersagewert = P (K+ | T+) : Der pos.VHW ist die Wahrscheinlichkeit dafür, dass eine positiv getestete Person tatsächlich erkrankt ist. (auch: positiver prädiktiver Wert / positive predictive value; PPV )
negativer Vorhersagewert = P (K- | T-) : Der neg.VHW ist die Wahrscheinlichkeit dafür, dass eine negativ getestete Person tatsächlich nicht erkrankt ist. (auch: negativer prädiktiver Wert / negative predictive value; NPV )
Diese beiden Werte hängen sehr stark von der Prävalenz in der betrachteten Gruppe ab!
negativer/positiver Vorhersagegewinn = P(K+ | T+) - P(K+) / P(K- | T-) - P(K-) : Der Vorhersagegewinn eines Tests gibt demnach die Erhöhung der Erkenntniswahrscheinlichkeit für Krankheit oder Nichtkrankheit bei einem entsprechenden Testausfall an. Die Summe der beiden Werte ergibt den gesamten Vorhersagegewinn des Tests.
Ein älteres, aber sehr gutes Lernprogramm zu den Diagnostischen Tests ist "Visual Bayes", das an der Universität in Freiburg entwickelt wurde.
Vorhersagewert veranschaulichen und bestimmen
Vorhersagewert - Baumdiagramm mit Schieberegler
Vorhersagewert - graphisch veranschaulicht
|
Hier können Sie das Programm Z_Mathematik herunterladen (z_mathematik.zip), in welchem das Zusammenspiel zwischen Baumdiagramm und Vier- bzw. Sechsfeldertafel demonstriert wird. Wählen Sie im Menü "Stochastik I" den Punkt "Baumdiagramm und Vier-/sechsfeldertafel (Demonstration)":
Wählen Sie im zugehörigen Untermenü "Baumdiagramm in duales Baumdiagramm und Vier-/Sechsfeldertafel":
Durch Drücken des Button "Demonstration" werden die oben ausgeführten Schritte 1 bis 4 demonstriert. |
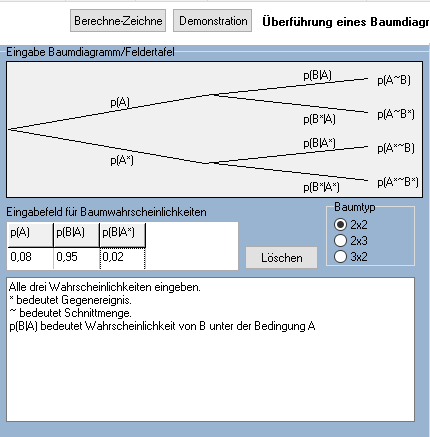
Im sich öffnenenden Fenster wählen Sie Baumtyp 2x2 und geben die Wahrscheinlichkeiten p(A), p(B|A) sowie p(B|A*) ein (D+ entspricht A, T+ entspricht B, D- entspricht A*).
|


 Unterscheidung von P(B | A) und P(B und A)
Unterscheidung von P(B | A) und P(B und A)