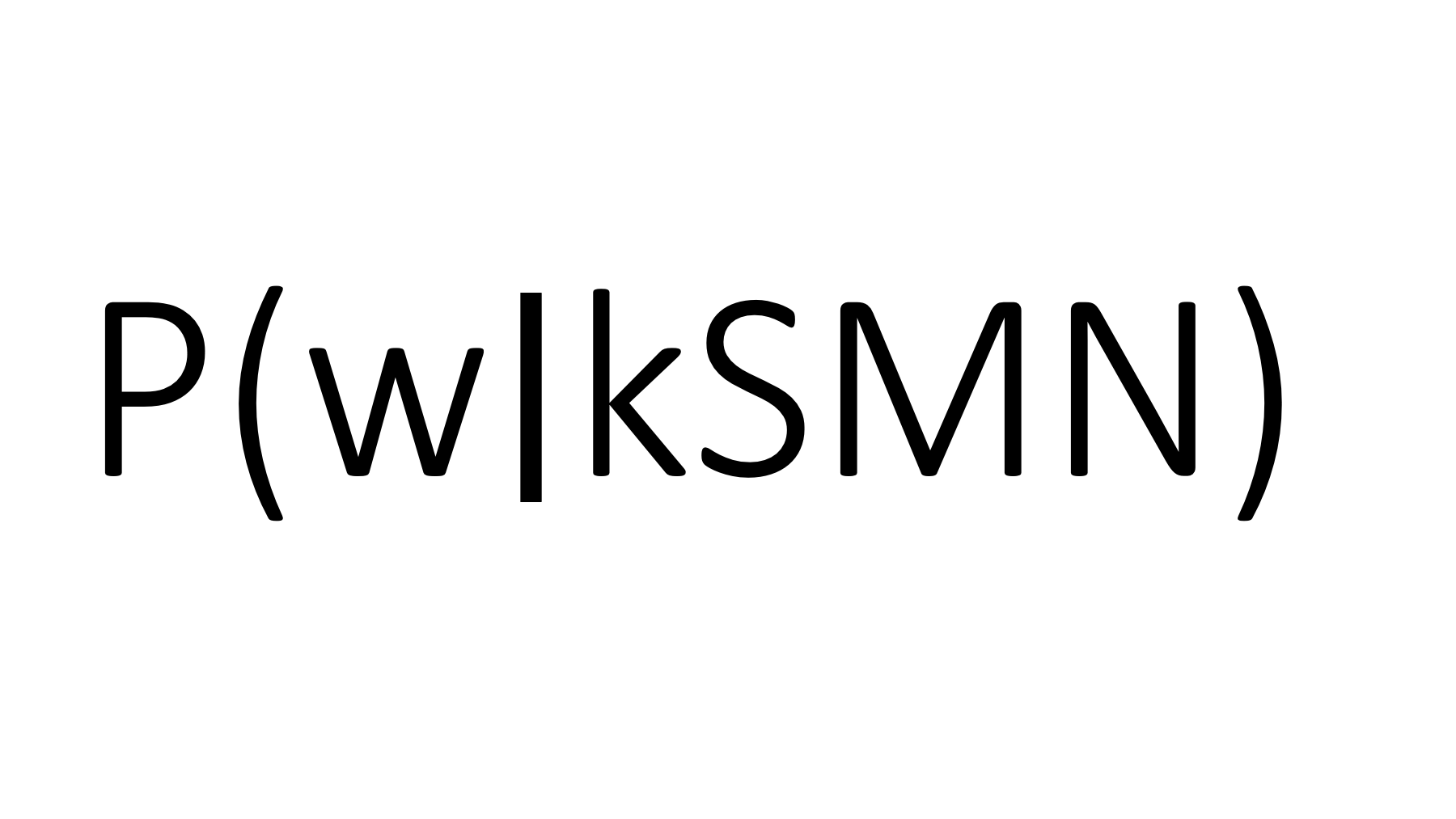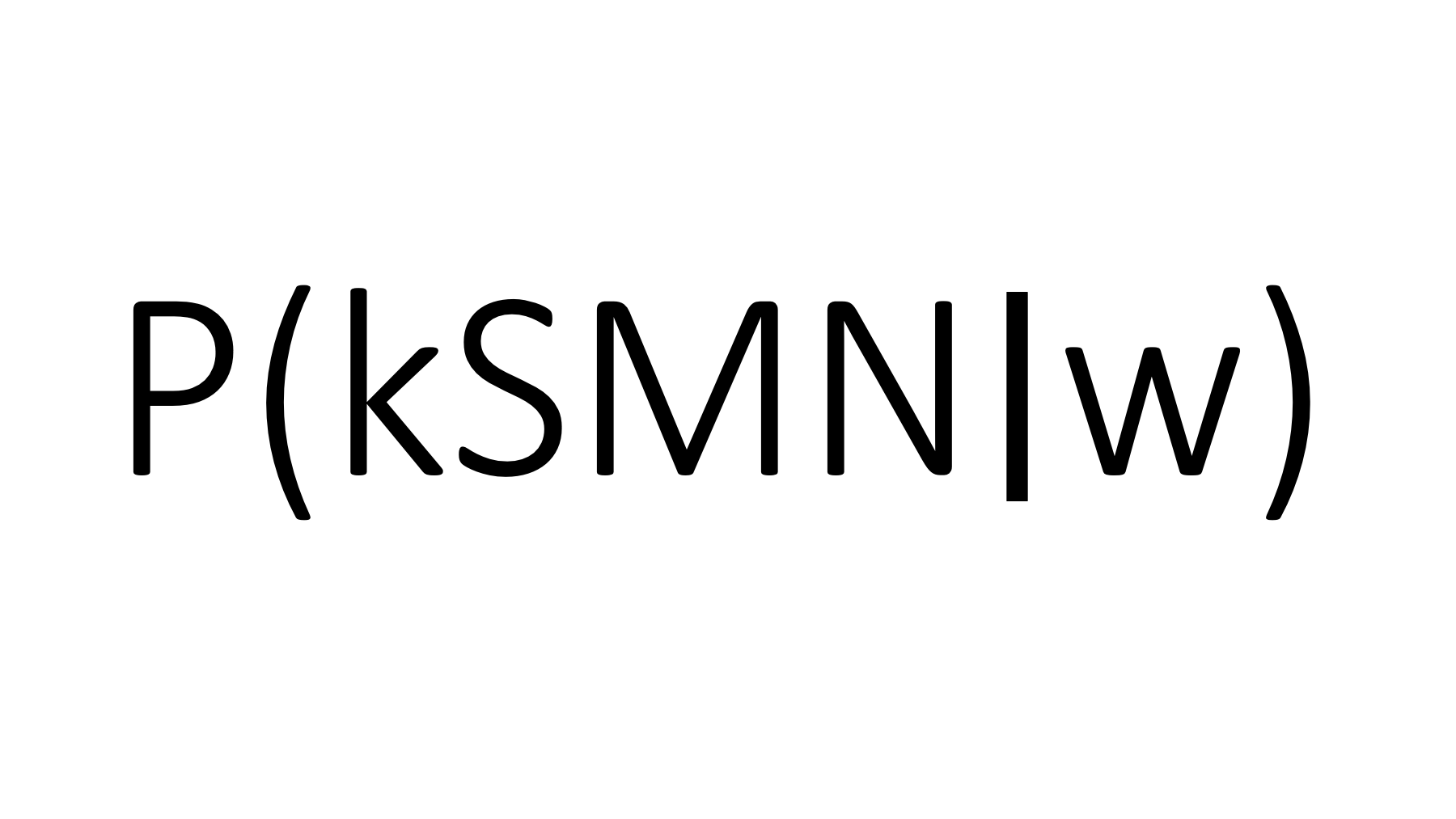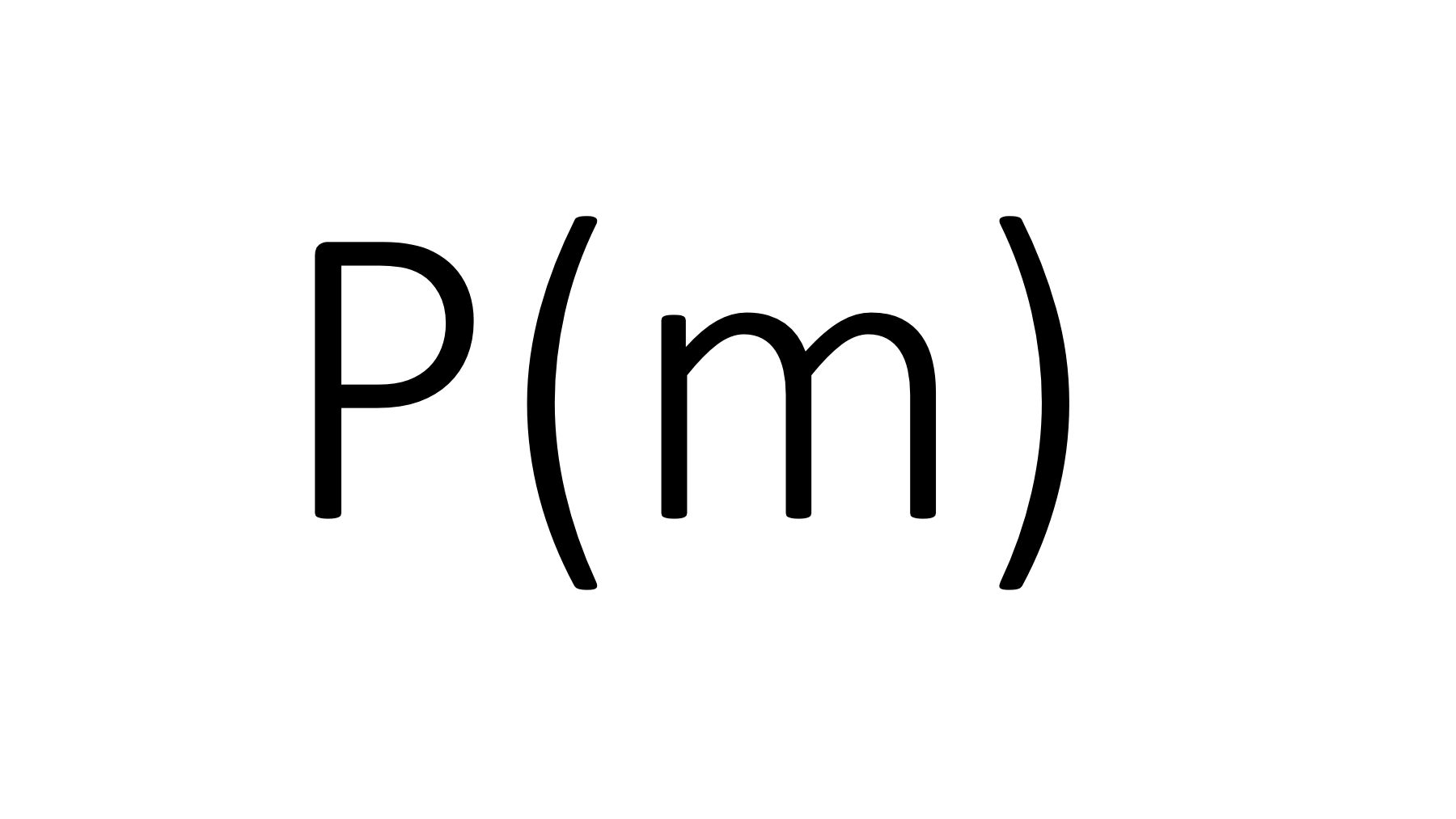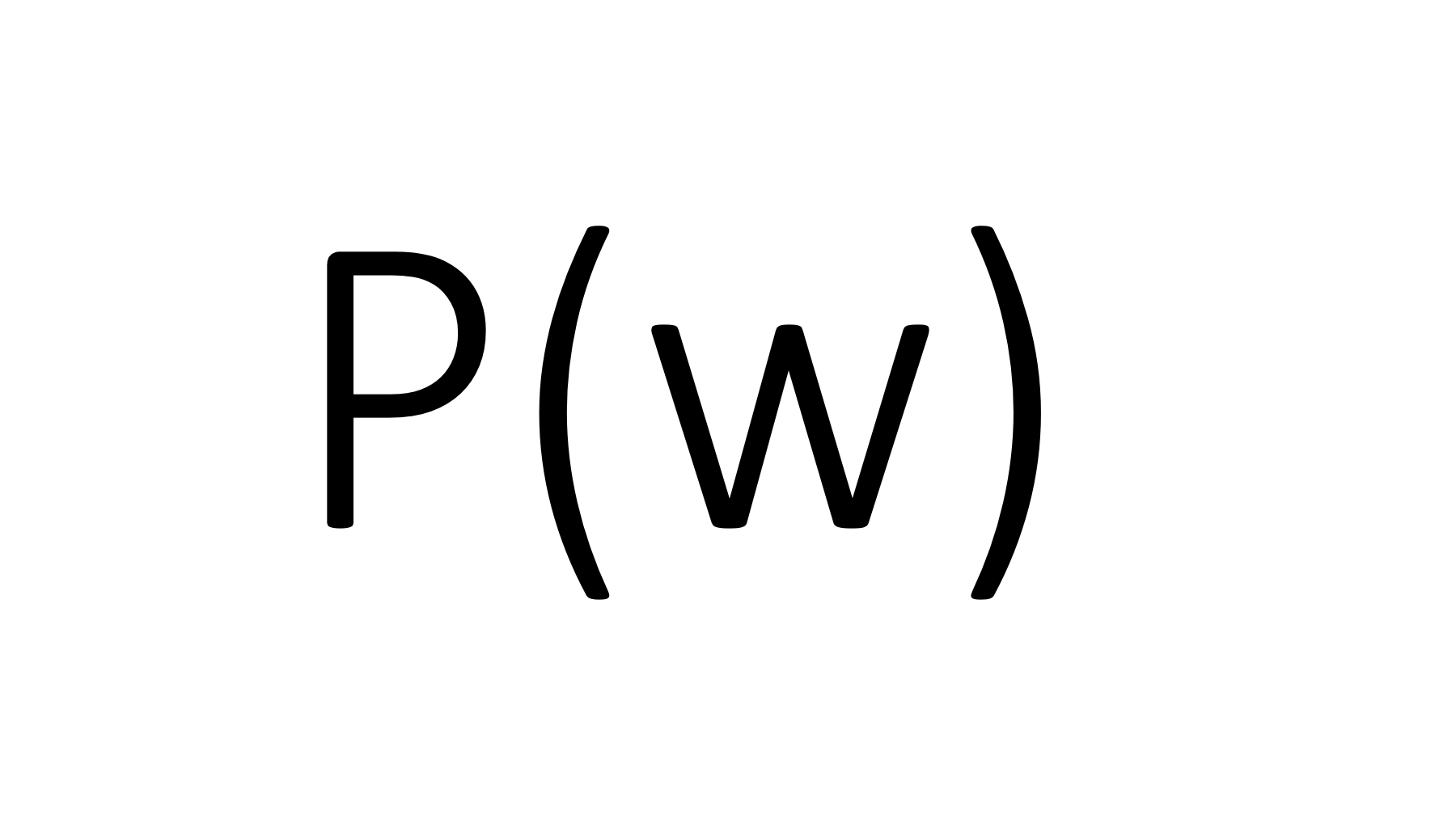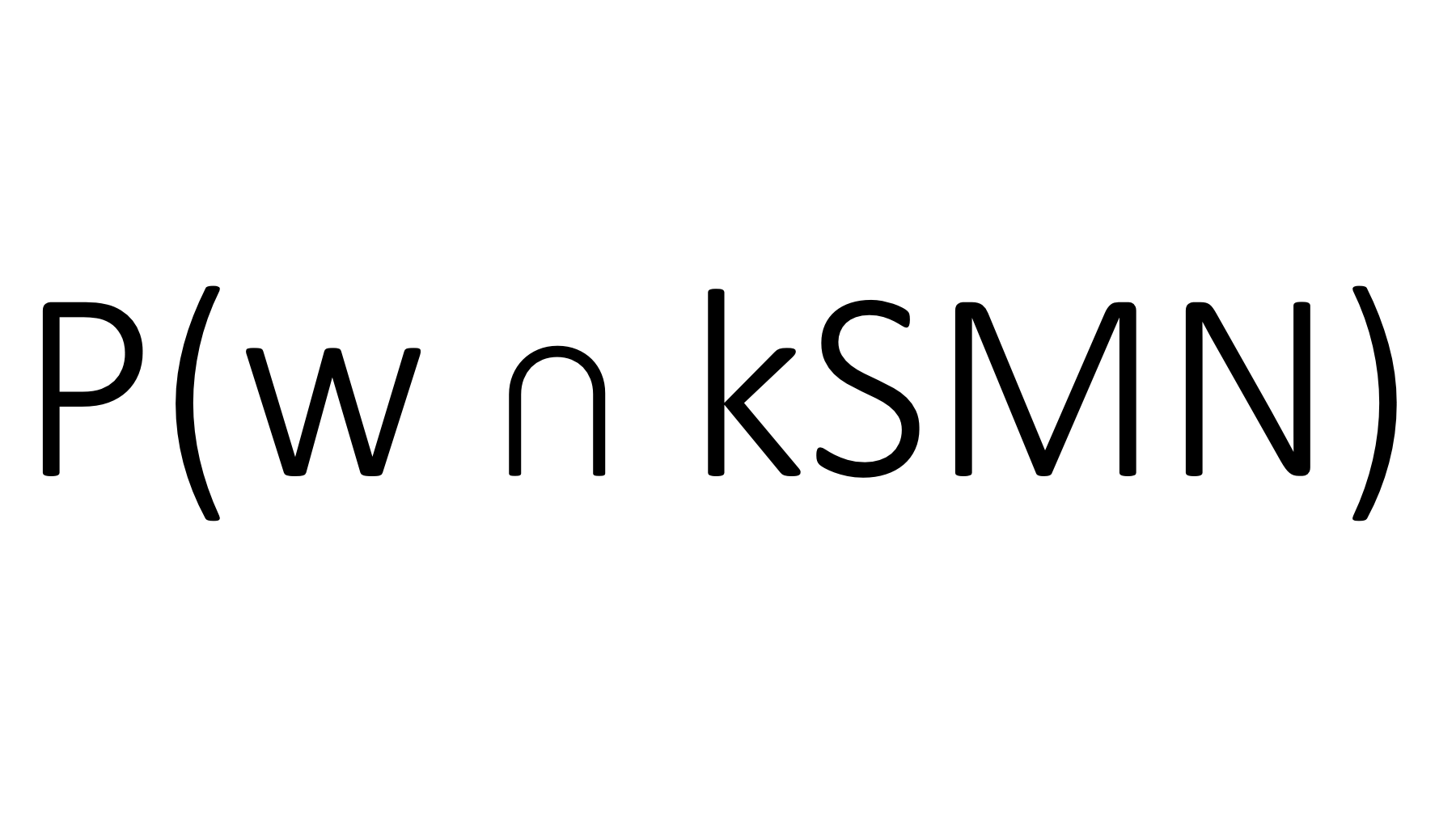Quelle: https://nwm2.net-schulbuch.de/index.php
Druckversion vom 15.05.2024 23:31 Uhr
Startseite
Einführungsphase
Stochastik
Bed. Wahrscheinlichkeit
Bayes-Wahrscheinlichkeit
Bedingte Wahrscheinlichkeiten & der Satz von Bayes - Aufgaben 1
 Aufgabe A1 Aufgabe A1 |
|
Blutspenden werden auf Diabetes untersucht, eine Krankheit, die mit ca. 8 % in der Bevölkerung verbreitet ist.
Der Test erkennt an Diabetes Erkrankte mit einer Wahrscheinlichkeit von 98 %, während 1 % der Testpersonen als Diabetiker eingestuft wird, obwohl sie es nicht sind.
- Stellen Sie ein Baumdiagramm zu dem Sachverhalt auf.
- Errechnen Sie die Wahrscheinlichkeit für das Testergebnis „Diabetiker".
- Berechnen Sie die Wahrscheinlichkeit dafür, dass ein positiv Getesteter tatsächlich nicht erkrankt ist.
Was ist bereits sicher eingetreten?
Eine Person wurde bereits positiv getestet und dann möchte man wissen, ob diese Person tatsächlich nicht erkrankt ist. Also die Wahrscheinlichkeit, dass man tatsächlich "nicht krank" ist unter der Bedingung, dass der Test positiv (T+) ist. Sprich "P nicht krank unter der Bedingung T+", d.h. P(nicht krank|T+).
|
 Aufgabe A2 Aufgabe A2 |
|
Betrachten Sie den folgenden Drogentest zur Prüfung auf Ecstasy.
Geben Sie die folgenden Wahrscheinlichkeiten an und erläutern Sie diese in Worten:
-
Erläutern Sie die Bedeutung der folgenden Angaben:
`P(E+) = 1 % `
`P(T+|E+) = 96 %`
`P(T-|E-) = 98 %`
E+ : Eine Person hat Ecstasy konsumiert.
E- : Eine Person hat kein Ecstasy konsumiert.
T+ : Der Drogentest fällt positiv aus.
T- : Der Drogentest fällt negativ aus.
- Erstellen Sie ein vollständiges Baumdiagramm mit den Daten aus a.
- Füllen Sie die nachfolgende Vierfeldertafel aus und erläutern Sie, warum man erst das Baumdiagramm aufstellen muss.
-
Geben Sie den Wert für die jeweilige Wahrscheinlichkeit an und erläutern Sie seine Bedeutung:
`P(E+ `und ` T-)`
`P(E- `und ` T-) `
- Berechnen Sie `P(E+|T+)` und `P(E-|T+)` und erläutern Sie die Bedeutung der beiden Wahrscheinlichkeiten.
|
 Aufgabe A3 Aufgabe A3 |
|
Ein Supermarkt verwendet für die Bearbeitung zurückgegebener Pfandflaschen eine Maschine.
Diese akzeptiert einwandfreie Flaschen (Annahme) mit 95 % Sicherheit, deformierte Flaschen (Zurückweisung) werden mit 90 % Sicherheit erkannt.
- Stellen Sie ein Baumdiagramm zum Sachverhalt auf, wenn erfahrungsgemäß 20 % der abgegebenen Flaschen nicht einwandfrei sind.
- Eine Flasche wird abgewiesen. Berechnen Sie die Wahrscheinlichkeit dafür, dass die Flasche trotzdem in Ordnung ist.
|
 Aufgabe A4 Aufgabe A4
|
|
Ein anderer Supermarkt verwendet für die Bearbeitung zurückgegebener Pfandflaschen eine qualitativ andere Maschine.
Diese akzeptiert einwandfreie Flaschen (Annahme) mit 99 % Sicherheit, deformierte Flaschen (Zurückweisung) werden mit 97 % Sicherheit erkannt.
- Stellen Sie ein Baumdiagramm zum Sachverhalt auf, wenn rund 90 % einwandfreie Flaschen abgegeben werden. Arbeiten Sie diesmal mit absoluten Häufigkeiten. Gehen Sie dazu von 100.000 abgegebenen Flaschen aus.
- Eine Flasche wird akzeptiert. Berechnen Sie die Wahrscheinlichkeit dafür, dass die Flasche trotzdem deformiert ist.
|
 Aufgabe A5 Aufgabe A5 |
|
Wird jemand auf Hepatitis C (HCV) untersucht, so werden immer zwei Tests gemacht. Beachten Sie dazu Aufgabe 6.
Der erste Test (Elisa) weist bei Nicht-Infizierten in Deutschland eine falsch-positive Rate von 1 % auf.
Die Wahrscheinlichkeit, dass ein HCV-positiver Mensch auch positiv getestet wird, liegt bei 98 %.
Die Erkrankungsrate (Prävalenz) in Deutschland liegt bei etwa 0,5 %.
- Stellen Sie ein Baumdiagramm zum Sachverhalt auf.
- Berechnen Sie die Wahrscheinlichkeit für einen positiven Test.
- Berechnen Sie die Wahrscheinlichkeit dafür, dass eine positiv getestete Person tatsächlich nicht erkrankt ist.
|
 Aufgabe A6 (Hinweis: erst Aufgabe 5 bearbeiten) Aufgabe A6 (Hinweis: erst Aufgabe 5 bearbeiten) |
|
Erhält ein Proband beim ersten HCV-Test ein positives Ergebnis, so wird ein zweiter Test gemacht, der HCV-Erkrankte mit 99,9 % Sicherheit als erkrankt diagnostiziert und Nicht-Erkrankte mit 99,8 % Sicherheit als nicht erkrankt erkennt.
- Begründen Sie P(HCV+)=0,33
Das Baumdiagramm zu Test 1 mit auf 3 Nachkommastellen gerundeten Ergebnissen: 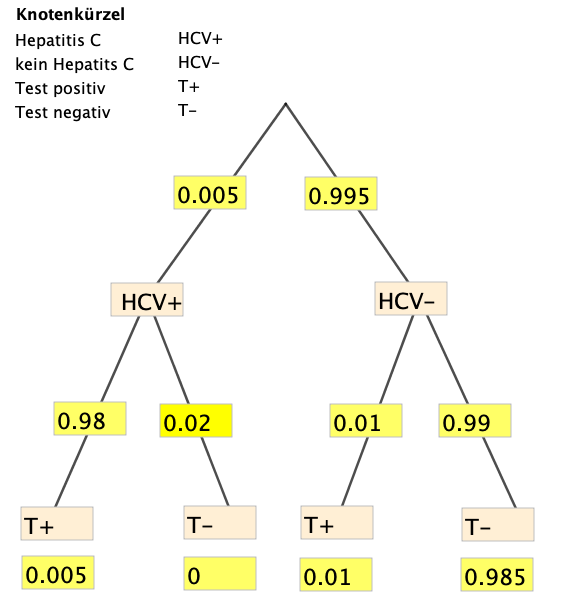
- Geben Sie das Baumdiagramm für diesen 2. Test an.
- Berechnen Sie jetzt die Wahrscheinlichkeit für ein positives Testergebnis.
- Berechnen Sie die Wahrscheinlichkeit für eine tatsächlich vorliegende HCV-Infektion bei einem positiven zweiten Test.
|
 Aufgabe A8 Aufgabe A8 |
|
Der schweizerische Pharmakonzern F. Hoffmann-La Roche AG aus Basel hat im Roche-Entwicklungslabor im oberbayerischen Penzberg einen neuen Bluttest für den Antikörpernachweis bei SARS-CoV-2 ("Corona-Virus") entwickelt, der als Laborbluttest innerhalb von wenigen (ca. 3) Stunden bis zu 100 Nachweise führen kann. Die Testdaten wurden auf einer Pressekonferenz vorgetragen. (s.Artikel rechts)
Nutzen Sie bei der Bearbeitung der Aufgabe diese Ereignisse:
T+ / T- : Der Test zeigt ein positives / negatives Ergebnis
A+ / A- : Der Proband hat Antikörper / keine Antikörper
- Formulieren Sie die im Artikel angeführten Begriffe Sensitivität und Spezifität als Wahrscheinlichkeiten.
- Beschreiben Sie kurz, wie der Hersteller den Spezifitätswert nachweisen könnte und geben Sie mögliche Fehlerquellen und Schwierigkeiten an.
- Geben Sie Zahlenbeispiele an, die die Aussage "zehn- bis zwanzigmal zuverlässiger" stützen würden.
- Weisen Sie nach, dass man vollständig sicher sein kann, dass man keine Antikörper besitzt, wenn der Test im Ergebnis negativ ist.
- Berechnen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Proband tatsächlich Antikörper besitzt, wenn der Test positiv ist und der Proband aus Gangelt [Gemeinde im Kreis Heinsberg mit einem "Durchseuchungsgrad" von ca. 15% lt. der Heinsberg-Studie aus Bonn.] bzw. Rostock [ca. 0,5% "Durchseuchung" als vorsichtige Schätzung der zum Zeitpunkt der Testvorstellung Infizierten.] stammt.
- Bewerten Sie die unterschiedlichen Ergebnisse aus d. im Hinblick auf die Nutzungsmöglichkeiten und Einsatzgebiete des Tests.
|

Auszüge aus einem online-Artikel der ZEIT vom 07.05.2020
Der Antikörpertest
… Ein neuer Antikörpertest der Firma Roche könnte die Antwort bringen. Der Test erreiche ein neues Qualitätsniveau, sagte Christoph Franz, der Verwaltungsratsvorsitzende des Unternehmens, …
Bei der Prüfung hat der Test jede Blutprobe von mit Covid-19 Infizierten korrekt identifiziert. Die sogenannte Sensitivität erreicht also 100 Prozent. Wichtiger aber ist die Spezifität: … Laut Roche sind es 99,8 Prozent. … Damit wäre Roches Verfahren zehn- bis zwanzigmal zuverlässiger als andere derzeit angebotene Tests. …
|
 Aufgabe A9 Aufgabe A9 |
|
Die folgende Vierfeldertafel bezieht sich auf Menschen mit einem Internetzugang in Deutschland und einer Untersuchung zur Nutzung von Social-Media.
|
 |
|
- Berechnen Sie die fehlenden Felder in der Vierfeldertafel.
- Bestimmen Sie `P(m)` und `P(SMN)`.
- Berechnen Sie `P(w|kSMN)` und `P(kSMN|w)`.
Geben Sie Ihre Werte in die GeoGebra-App zu Vierfeldertafeln ein und prüfen Sie Ihre Ergebnisse zu b und c. Hinweis zur Nutzung von GeoGebra-Applets: Nutzen Sie die Split-Screen Funktion Ihres Browsers, sodass sie sich Aufgabe und Applet nebeneinander auf einem Bildschirm anzeigen lassen können.
- Ordnen Sie die Sprechweisen den entsprechenden Schreibweisen zu.
|


 Aufgabe A9
Aufgabe A9 


 Baumansatz
Baumansatz Hier ist die Vorlage für eine Vierfeldertafel mit absoluten Häufigkeiten
Hier ist die Vorlage für eine Vierfeldertafel mit absoluten Häufigkeiten