Druckversion vom 15.05.2024 14:46 Uhr
Startseite Einführungsphase Stochastik Bed. Wahrscheinlichkeit Bayes-Wahrscheinlichkeit
Bedingte Wahrscheinlichkeiten & der Satz von Bayes - Basisaufgaben
 Aufgabe B1 Aufgabe B1 |
||||||||||||||||||
|
A und B seien zwei Ereignisse.
| ||||||||||||||||||
Mit diesem Chat können Benutzer des Net-Schulbuches, die derselben Lehrkraft zugeordnet sind, miteinander chatten. Dabei gelten folgende Regeln:
 Aufgabe B1 Aufgabe B1 |
||||||||||||||||||
|
A und B seien zwei Ereignisse.
| ||||||||||||||||||
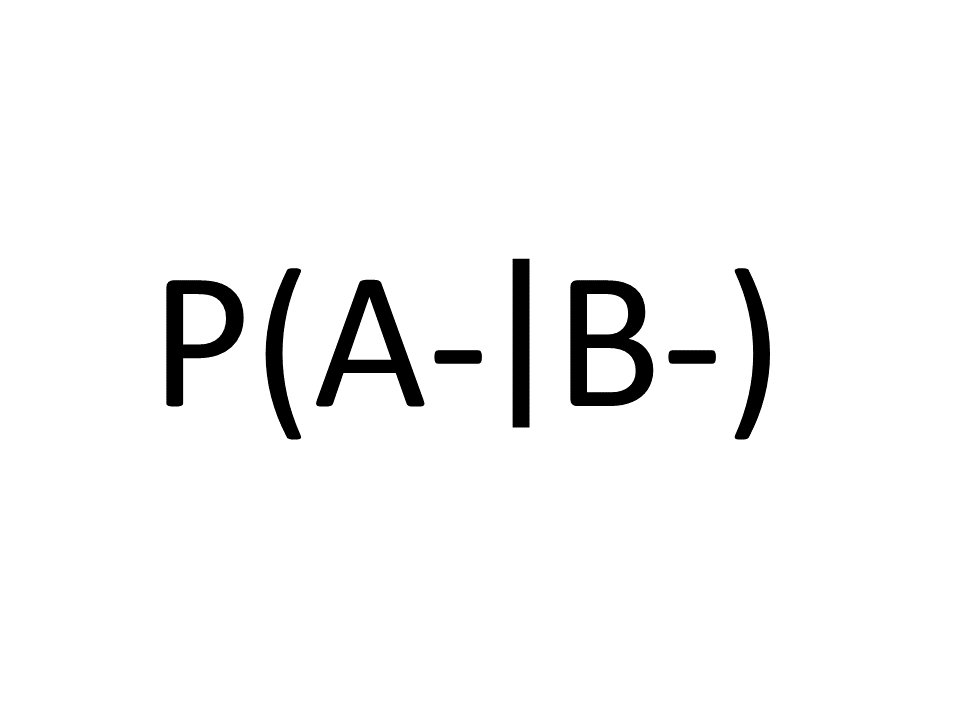 |
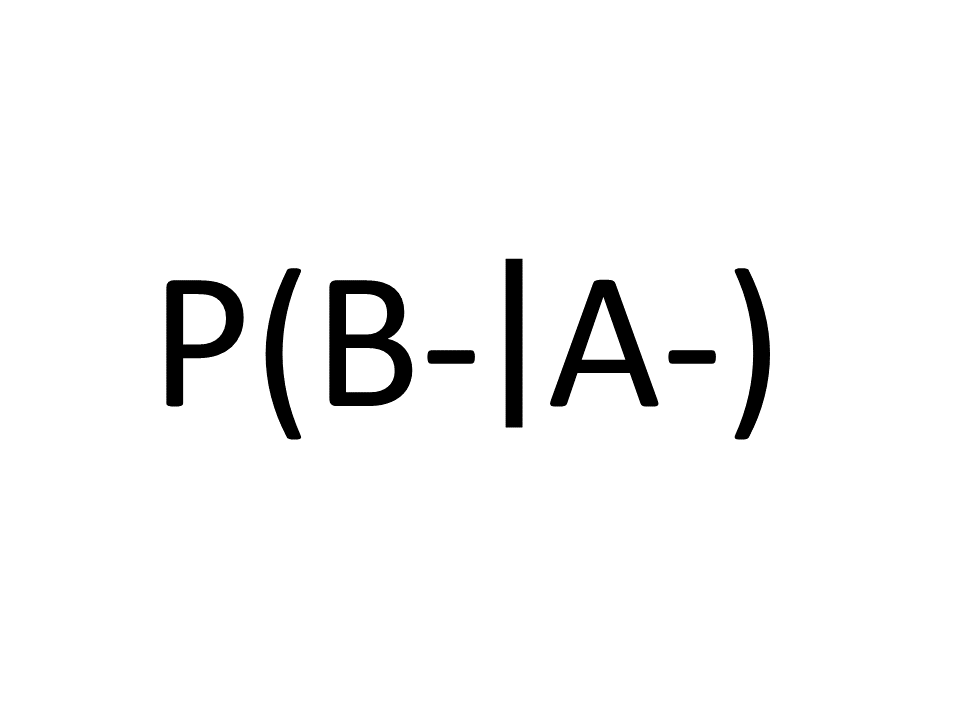 |
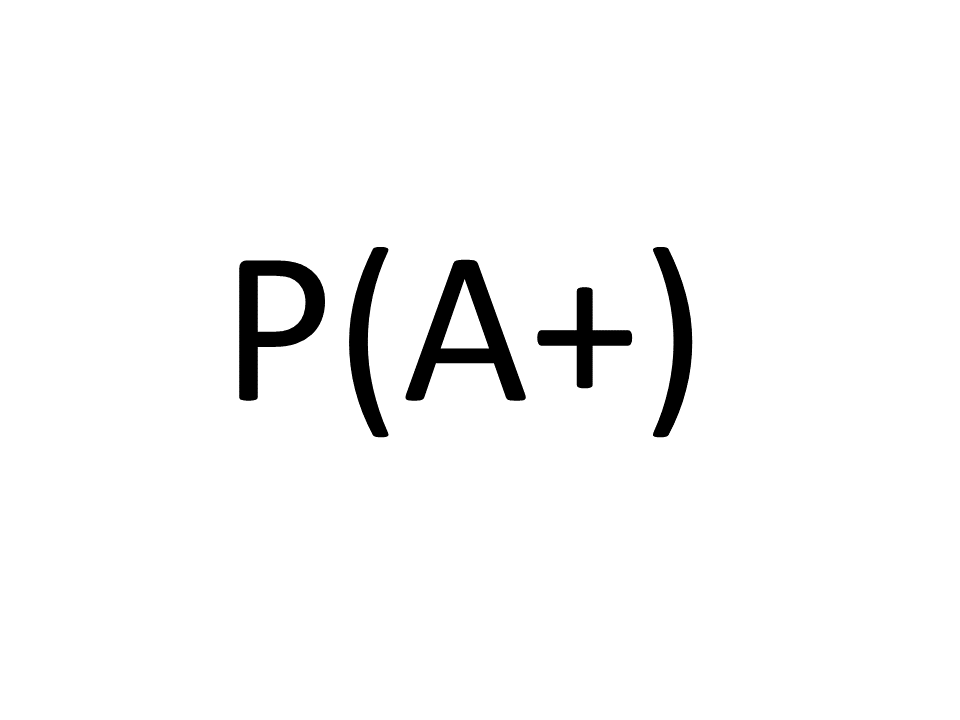 |
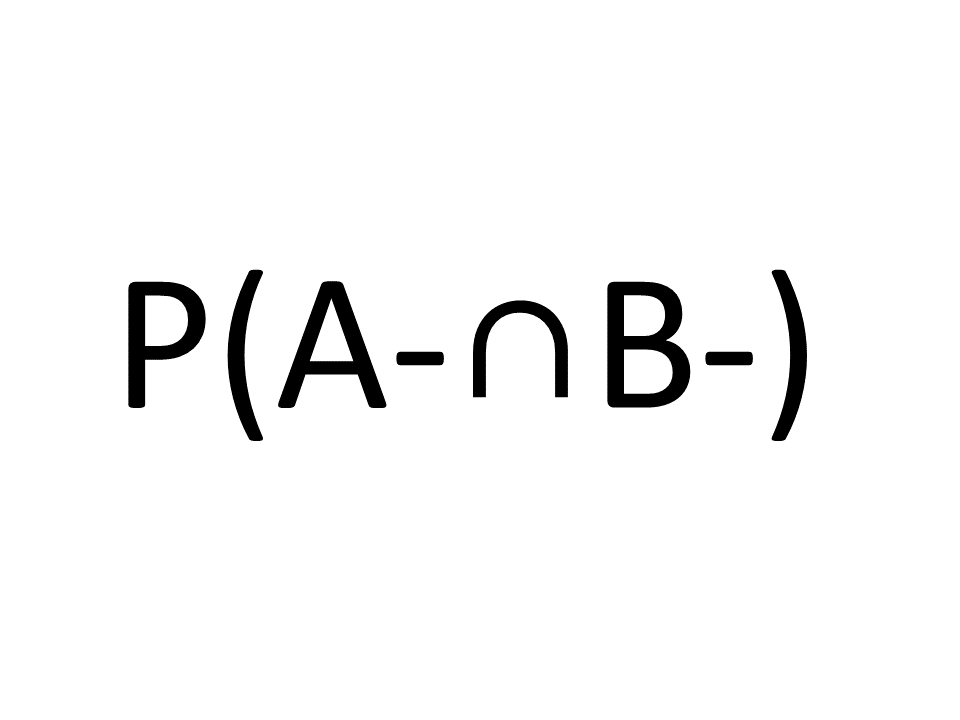 |





 Aufgabe B2 Aufgabe B2 |
|
In Deutschland leben rund 15% der Menschen in Ostdeutschland, jeder 25. dort ist Ausländer. In Westdeutschland liegt der Anteil bei rund 11,7% (Stand 2016).
|
 Aufgabe B3 Aufgabe B3 |
|
|
Die Produzenten der Fernsehsendung 'Visite' im NDR wollen mehr über ihre Zuschauer wissen. Sie haben deshalb eine Umfrage durchführen lassen, die folgende Informationen lieferte:
Informationen zur Sendung Visite - das Gesundheitsmagazin. |
|
 Aufgabe B4 Aufgabe B4 |
|
|
Das Statistische Bundesamt meldet: Im Jahr 2018 gab es insgesamt 288184 Unfälle mit Personenschaden (ohne Autobahnen). Innerorts gab es 213124 solcher Unfälle, dabei verloren 984 Menschen ihr Leben. Außerorts wurden trotz deutlich geringerer Unfallzahlen 4470 Menschen getötet.
Viele weitere Zahlen beim Statistischen Bundesamt! |
|
|
20% der Bevölkerung eines Landes sind über 65 Jahre alt. Sie werden hier Senioren (Abkürzung: S+) genannt. 10% der Bevölkerung sind Senioren und nutzen das Internet. Insgesamt sind 85% der Bevölkerung Internetnutzer (Abkürzung: I+).
Überlegen Sie auch bei anderen Aufgaben, welches Verfahren Ihnen am einfachsten erscheint! |