Druckversion vom 27.07.2024 14:58 Uhr
Startseite Einführungsphase Stochastik Bed. Wahrscheinlichkeit Bayes-Wahrscheinlichkeit
Bedingte Wahrscheinlichkeiten & der Satz von Bayes - Erforschen 1
|
Seit 2018 kann man in Deutschland sogenannte Heimtests für HIV und andere sexuell übertragbare Krankheiten kaufen. Mit so einem Heimtest kann man sich innerhalb von wenigen Minuten zuhause selbst auf eine HIV-Infektion untersuchen. Aber Vorsicht: Wie zuverlässig ist das Testergebnis? Und was bedeutet überhaupt ein positives Testergebnis?
Ein häufig gekaufter Heimtest wirbt mit folgenden Werten:
Aus Daten des Robert-Koch-Instituts kann man ableiten, dass der Anteil der HIV-infizierten Menschen in Deutschland bei `0.01 %` liegt (sogenannte Erkrankungsrate oder Prävalenz).
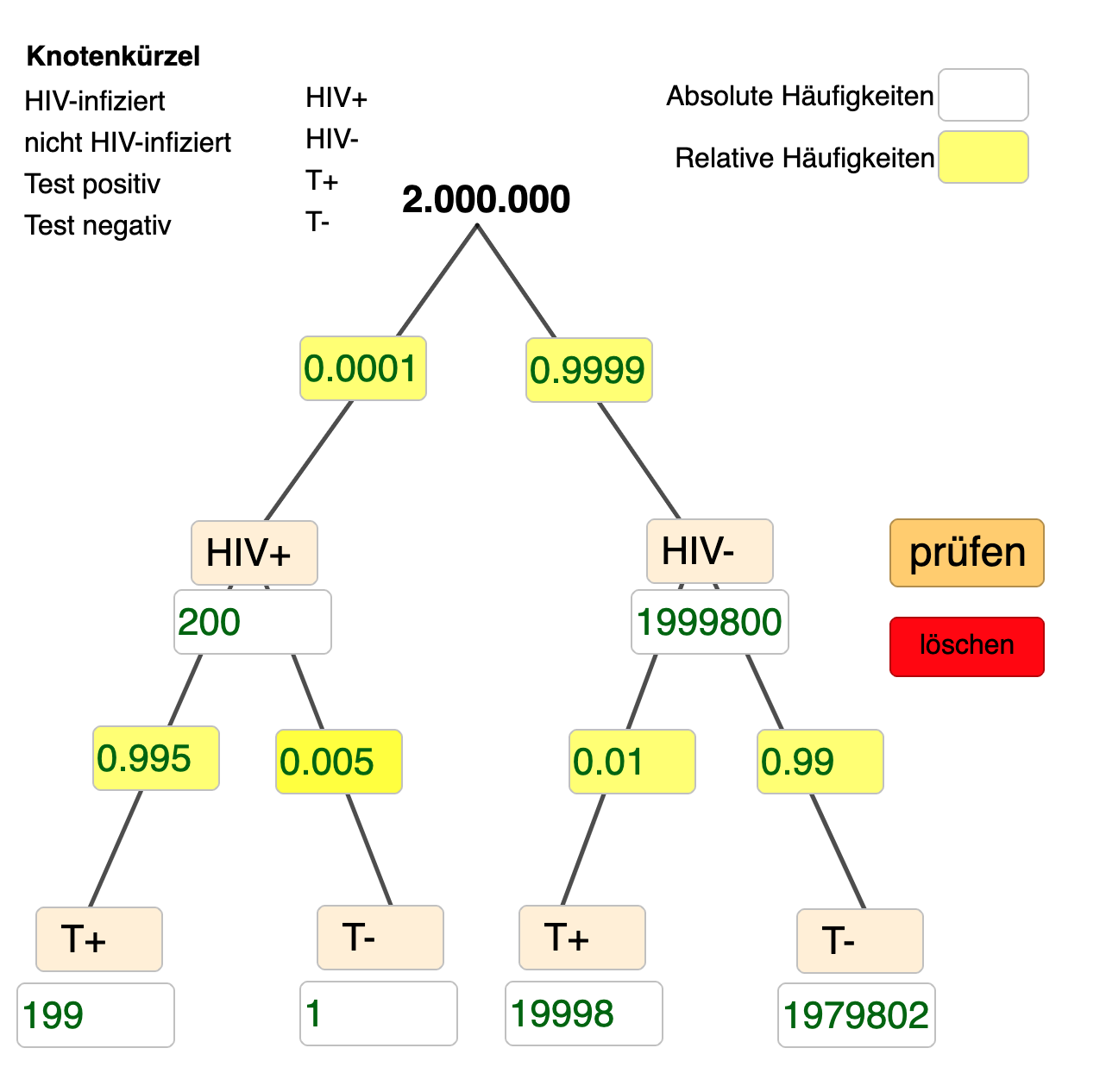
In die gelben Felder können Sie die Wahrscheinlichkeiten bzw. relativen Häufigkeiten als Dezimalzahl eintragen (d.h. `0.02 %` als `0.0002`). In die weißen Felder können Sie die Anzahl der jeweils Betroffenen (absolute Häufigkeiten) eintragen.
Versuchen Sie diese Aufgabe einmal mit einer Vierfeldertafel zu bearbeiten! Können alle angegebenen Werte in einer Vierfeldertafel eingetragen werden? Überlegen Sie sich stets, ob Sie eine Aufgabe eher mit einem Baumdiagramm oder einer Vierfeldertafel bearbeiten möchten... bzw. können.
|
|
Sie können den Zusammenhang zwischen der Prävalenz und dem positiven Vorhersagewert ganz allgemein mit der nachfolgenden GeoGebra - APP erkunden.
Wie beeinflusst die Prävalenz den Vorhersagewert?
Formulieren Sie vorweg eine Vermutung und anschließend Ihre Erkenntnis.
Der negative Vorhersagewert:
Manche Hersteller formulieren auf ihrer Homepage: "Wenn der Test negativ ist, können Sie davon ausgehen, dass Sie nicht HIV-infiziert sind." Weisen Sie durch Rechnung nach, dass der Satz mit hoher Sicherheit richtig ist.
Berechnung mit relativen statt absoluten Häufgkeiten:
Sie können die Vorhersagewerte statt mit absoluten Häufigkeiten (Anzahlen) auch mithilfe der Pfadwahrscheinlichkeiten berechnen. Schreiben Sie den entsprechenden Term für den negativen oder positiven Vorhersagewert mit Pfadwahrscheinlichkeiten auf und begründen Sie, warum sowohl bei den absoluten Häufigkeiten als auch bei Nutzung der Pfadwahrscheinlichkeiten dasselbe Ergebnis herauskommt.
Bei Untersuchungen von Schnelltest werden einige spezielle Begriffe benutzt. Hier finden Sie eine Übersicht mit den Bedeutungen einzelner Begriffe:
K+ / K- : Die Krankheit ist vorhanden / nicht vorhanden
T+ / T- : Der Test fällt positiv (er zeigt die Krankheit an) / negativ (er zeigt die Krankheit nicht an) aus.
Gütekriterien eines Tests: [Diese Werte werden in Studien an Erkrankten bzw. Nichterkrankten ermittelt.]
Sensitivität = P(T+ | K+) : Die Sensitivität eines Tests ist die Wahrscheinlichkeit dafür, dass der Test bei einem Erkrankten ein positives Ergebnis anzeigt. [" Der Test ist sensibel für diese Krankheit."]
Spezifität = P(T- | K-) : Die Spezifität eines Tests gibt die Wahrscheinlichkeit dafür an, dass der Test bei einem Nichterkrankten ein negatives Testergebnis anzeigt. ["Der Test reagiert nur speziell auf diese Krankheit."]
Für die getesteten Personen sind normalerweise zwei andere Wahrscheinlichkeiten wichtiger:
positiver Vorhersagewert = P (K+ | T+) : Der pos.VHW ist die Wahrscheinlichkeit dafür, dass eine positiv getestete Person tatsächlich erkrankt ist. (auch: positiver prädiktiver Wert / positive predictive value; PPV )
negativer Vorhersagewert = P (K- | T-) : Der neg. VHW ist die Wahrscheinlichkeit dafür, dass eine negativ getestete Person tatsächlich nicht erkrankt ist. (auch: negativer prädiktiver Wert / negative predictive value; NPV )

Weitergehende Informationen zu den HIV-Heimtests finden Sie hier.
Über HIV-Symptome.de
Zu den Rechnungen:
Bitte beachten Sie: Als Zwischenwerte bei der Berechnung z.B. der Vierfeldertafel treten Dezimalzahlen auf, die dem Kontext (Anzahl von Menschen) nicht gerecht werden. Sie werden dennoch nicht gerundet, erst die Lösung wird - falls es sich aus dem Sachzsammenhang ergibt - angepasst.
zu a.
0,01% von 2 Mio. sind 200 Personen.
Rechnung: `2.000.000 * 0,0001 =200`
zu b.
Von den 200 HIV-Infizierten bekommen 199 ein positives Testergebnis.
Rechnung: `200*0,995=199`
zu c.
Von den Gesunden erhalten 19998 ein positives Testergebnis.
Rechnung: `1.999.800 *0,01 = 19998`
Hier wird bereits das Problem des Testes ersichtlich.
zu d.
Gesucht ist `P(HIV+| T+)`.
`P(HIV+| T+)` ist die Wahrscheinlichkeit mit HIV infiziert zu sein unter der Bedingung, dass man ein positives Testergebnis bekommen hat.
Ein positives Testergebnis haben `199 + 19998 = 20 197` Untersuchte erhalten.
Nur `199` der Testergebnisse zeigten eine vorliegende HIV-Infektion richtig an.
Die Wahrscheinlichkeit errechnet sich dann als Anteil dieser an allen mit positivem Testergebnis.
Also: `P(HIV+|T+) = 199 / (199 + 19998) ~~ 0.0099 = 0.99 %`.
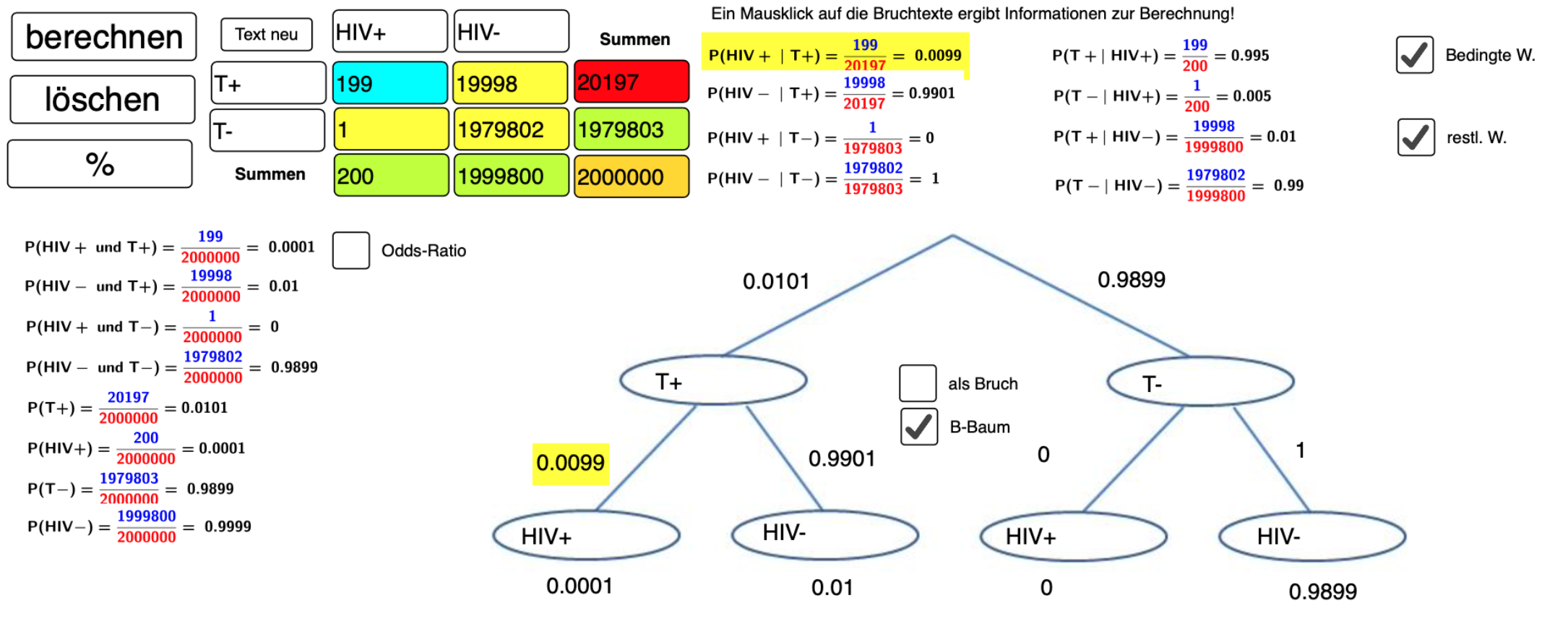
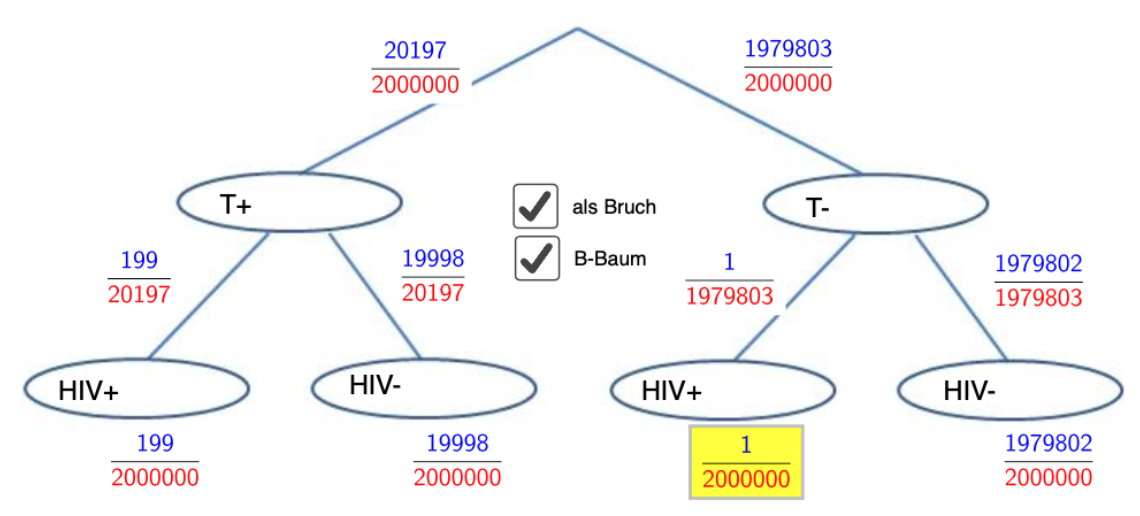
Die Wahrscheinlichkeit infiziert zu sein, ist durch die Bedingung eines positiven Testergebnisses von `0.01 %` auf fast `1 %` gestiegen, dennoch ist sie mit knapp `1 %` noch sehr gering.
Die Wahrscheinlichkeit, dass jemand mit HIV infiziert ist und ein positives Testergebnis bekommt, ist (mithilfe der Pfadregel) `0.0001*0.995 = 0.0000995`.
Die Wahrscheinlichkeit, dass jemand nicht mit HIV infiziert ist und ein positives Testergebnis bekommt, ist (mithilfe der Pfadregel) `0.9999*0.01 = 0.009999`
Daraus berechnet sich die Wahrscheinlichkeit, dass jemand HIV infiziert ist unter der Voraussetzung, dass der Test positiv war:
`P(HIV+|T+) = (0.0000995) / (0.0000995 + 0.009999) ~~ 0.0099 = 0.99 %`.
Bzw. mit der Vierfeldertafel oder dem umgekehrten Baumdiagramm:
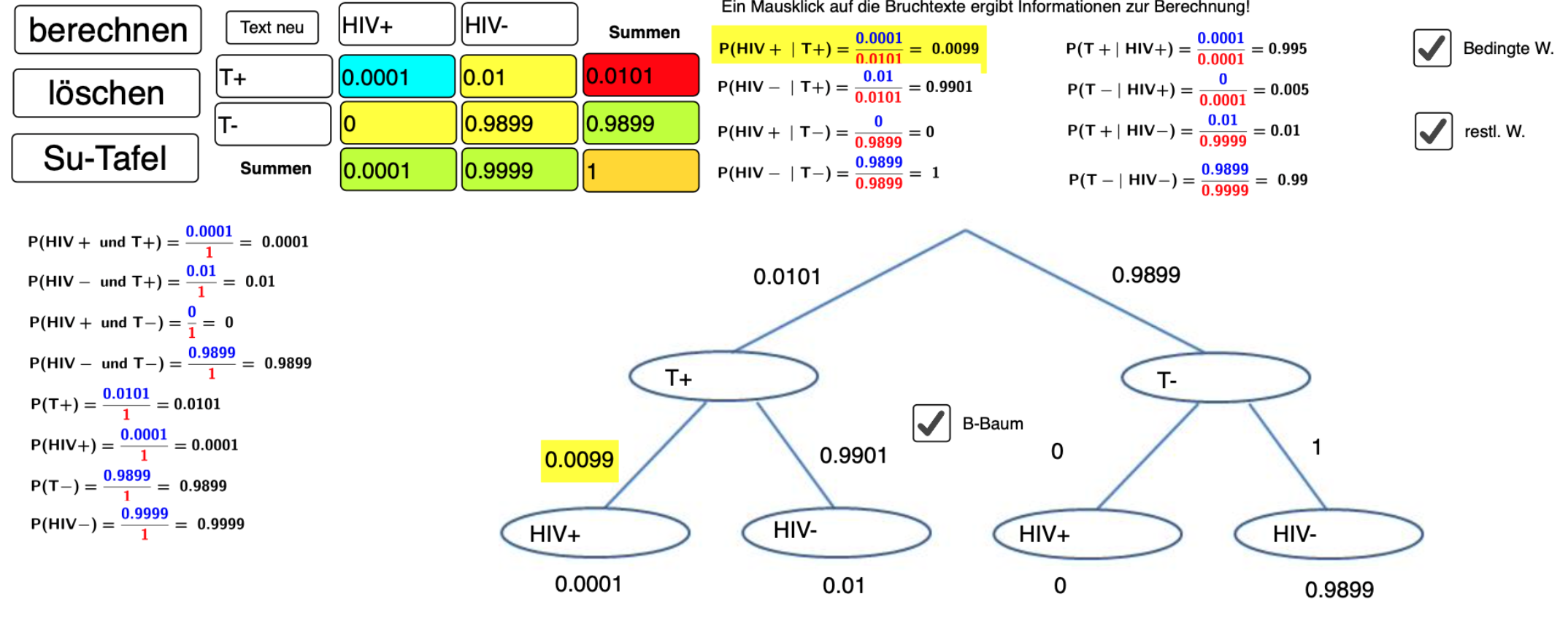
zu e.
Die Problematik ist oben schon angedeutet:
Es werden zwar fast alle Infizierten erkannt, aber viel zu viele Gesunde erhalten ein positives Testergebnis, was natürlich gewaltigen Stress verursacht.
Daher wird es an Gesundheitsämtern so gehandhabt, dass das Ergebnis "positiv" erst dann an den Getesteten herausgegeben wird, wenn ein Bestätigungstest auch positiv war.
Die Abhängigkeit des positiven Vorhersagewertes `P(HIV+|T+)` bzw. allgemein von `P(K+|T+)` deutet sich schon in Teilaufgabe d. an.
Mit der GeoGebra-APP können Sie nun die Prävalenz beliebig ändern und damit zeigen, dass der positive Vorhersagewert um so höher ist, je größer die Prävalenz ist.
zum negativen Vorhersagewert:
Von den Infizierten erhält eine Person ein falsch-negatives, von den Nicht-Infizierten erhalten `1979802` ein richtig negatives Testergebnis.
Also ist `P(HIV-|T-) = 1979802/(1+1979802) ~~ 0.999999 ~~ 99.99 %`.
Ein negativ getesteter Mensch ist also mit sehr hoher Wahrscheinlichkeit nicht HIV-infiziert.
Die Aussage der Testhersteller ist berechtigt.
zur Berechnung mit relativen statt absoluten Häufigkeiten:
Bei den Pfadwahrscheinlichkeiten werden die ermittelten Anzahlen jeweils durch `2.000.000` geteilt und dieser Wert kürzt sich dann wieder heraus.
Man erhält also für den negativen Vorhersagewert:
`P(HIV-|T-) = (0.989901)/ (0.0000005 + 0.989901) ~~ 0.999999`.
Die Berechnung des positiven Vorhersagewert finden Sie bei Teilaufgabe d).


 Warum ist hier ein Baumdiagramm und keine Vierfeldertafel?
Warum ist hier ein Baumdiagramm und keine Vierfeldertafel?