
Quelle: https://nwm2.net-schulbuch.de/index.php
Druckversion vom 15.05.2024 17:17 Uhr
Startseite
Einführungsphase
Stochastik
Bed. Wahrscheinlichkeit
Bayes-Wahrscheinlichkeit
Bedingte Wahrscheinlichkeiten & der Satz von Bayes - weitergehende Aufgaben
 Aufgabe W1 Aufgabe W1 |
|
Während der ELISA-Test auf Hepatitis C (HCV) bei Normalpersonen eine falsch-positive Rate von 2 % aufweist, liegt diese für Personen mit Immunschwäche (z. B. HIV) bei rund 20 %. Die Wahrscheinlichkeit, dass ein HCV-positiver Mensch auch positiv getestet wird, liegt für beide Gruppen bei 99 %. Die Verbreitung von HCV liegt laut Schätzungen des Robert Koch Institus in der Normalbevölkerung etwa bei 0,5%, in der Gruppe der Immunschwächepatienten liegen Prävalenzschätzungen bei bis zu 30%.
- Berechnen Sie die Wahrscheinlichkeit, tatsächlich HCV+ zu sein, wenn der ELISA-Test positiv ist (für Normalpersonen, für Menschen mit Immunschwäche).
- Berechnen Sie für beide Gruppen die Wahrscheinlichkeit, nicht infiziert zu sein, wenn der ELISA-Test negativ ausgeht.
- Erklären Sie den Unterschied zwischen P(HCV+ | T+) und P(T+ | HCV+).
ELISA - enzyme-linked immunosorbent assay
So wird ein Testverfahren bezeichnet, das Antikörper oder Antigene mit Hilfe von beteiligten Enzymen auch farblich nachweisen kann. ELISA-Tests gibt es für viele verschiedene 'Krankheiten'. |
 Aufgabe W2 Aufgabe W2 |
|
Nach Umfragen der Zeitschrift Brigitte sind rund 45 % der Frauen (sogenannte "Inzidenz"), die einen Schwangerschaftstest machen, tatsächlich schwanger. Die Sensitivität (P(T+|Schwangerschaft)) und die Spezifität (P(T-|keine Schwangerschaft)) des Tests betragen beide 99%.
- Berechnen Sie unter diesen Bedingungen den Informationsgewinn durch einen positiven bzw. negativen Test.
- Erklären Sie mathematisch, warum die Unsicherheit viel größer ist, wenn man nur von einer a priori-Wahrscheinlichkeit (Inzidenz) von 1 % ausgeht.
|
 Aufgabe W3 Aufgabe W3 |
|
Beim Down Syndrom ist das Chromosom 21 drei- statt zweimal vorhanden, weshalb man in solchen Fällen auch von Trisomie 21 spricht. Symbolisch wird daher der 21.3. als Trisomie21-Tag begangen.
Kinder, die mit dieser Anomalie geboren werden, brauchen in der Regel etwas länger um Schreiben oder Lesen zu lernen. In Deutschland werden jährlich nach unterschiedlichen Quellen etwa 800 bis 1200 Kinder mit dieser Behinderung geboren, insgesamt leben hier etwa 50000 Menschen mit Down Syndrom.
Als Risiko-Gruppe gelten insbesondere Mütter ab 35 Jahren. Beruhend auf Fallzahlen von 2016 kann man das Gesamtrisiko für Trisomie 21 mit 1 : 400, für Mütter unter 35 Jahren mit 1 : 888 und ab 35 Jahren mit 1 : 158 beziffern.
Anfang des 21. Jahrhunderts wurde als erste nicht invasive Methode zum vorgeburtlichen Nachweis der Trisomie-21 das erweiterte Ersttrimesterscreening (11. – 14. Schwangerschaftswoche) eingeführt. Dabei werden u.a. spezifische Eiweiße und Hormone im mütterlichen Blut bestimmt und mit Ultraschall die sogenannte „Nackentransparenz“ gemessen. Nach Angaben von Docplayer beträgt die Sensitivität dieses Verfahrens 85,6%, die Spezifität 95%.
- In der Gruppe der Mütter mit 35 Jahren und älter werden jährlich zwischen 200.000 und 220.000 Geburten registriert. Mit wie vielen Kindern mit Downsyndrom muss man jährlich rechnen?
- Bestimmen Sie den positiven Vorhersagewert (d.h. die Wahrscheinlichkeit, dass ein Kind mit einem positiven Erstsemesterscreening tatsächlich das Down Syndrom hat). Gehen Sie davon aus, dass die werdende Mutter 35 Jahre und älter ist.
- Die Deutsche Gesellschaft für Gynäkologie und Geburtshilfe e.V. schreibt in einer Empfehlung, dass man bei einem positiven Erstsemesterscreening ("erhöhtes Risiko") den nicht invasiven Pränataltest als Zweittest empfehlen könne. Dieser hat eine Sensitivität von 99,2 % und eine Spezifität von 99,91 %, muss aber bis jetzt noch selbst bezahlt werden. Begründen Sie durch Rechnung, welche Vorteile dieser zweite Test bringt.
- Zeigen Sie durch Rechnung, dass bei einem negativen Erstsemesterscreening kein weiterer Test nötig ist.
Das Thema Pränataldiagnostik wird in Deutschland heftig diskutiert. Sie könnten die Argumente von Befürwortern und Gegner zusammentragen und im Philosophie- oder Religionsunterricht weiter diskutieren.
|
 Aufgabe W4 : Antigentests Aufgabe W4 : Antigentests |
|
Das RKI hat die beiden nachfolgenden Grafiken am 10.12.2020 veröffentlicht. Sie sollen die Einordnung der Schnelltestergebnisse erlauben - links bei Massentests, rechts bei gezielten Tests (Menschen mit Symptomen).
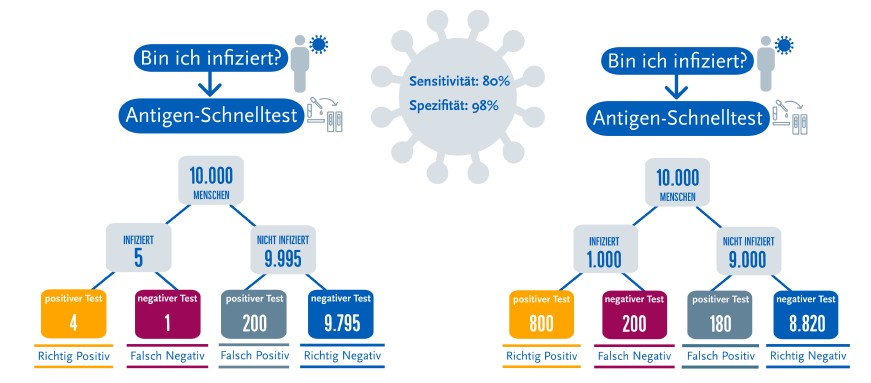
- Ermitteln Sie mit Hilfe der angegebenen Daten, mit welcher Prävalenz (Anteil der unentdeckt Infizierten) in den beiden Fällen gerechnet wird.
- Berechnen Sie für beide Fälle die Wahrscheinlichkeit, dass ein positiv Getesteter auch tatsächlich infiziert ist (positiver Vorhersagewert).
- Ermitteln Sie entsprechend den negativen Vorhersagewert.
- Viele Fachleute gehen davon aus, dass die vom RKI zugrunde gelegte Prävalenz für die Massentests zu niedrig ist. Zum Zeitpunkt der Veröffentlichung ging es von 300.000 aktiv Infizierten aus. Machen Sie auf der Basis eine eigene Abschätzung, indem sie eine Dunkelziffer von 5 voraussetzen. Diese Zahl wurde vom RKI immer mal wieder genannt und meint, dass auf einen nachgewiesenen Fall fünf unentdeckt Infizierte kommen. Nur letztere kommen ür einen Antigentest in Frage.
- Berechnen Sie auf dieser Basis ebenfalls den positiven und negativen Vorhersagewert.
- Formulieren Sie eine Empfehlung für jemanden, der ein positives (bzw. negatives) Testergebnis erhalten hat und dies nicht einordnen kann.
|
 Aufgabe W5 Aufgabe W5 |
|
Bertrandsches Schubfachproblem
(nach Joseph Bertrand, einem französischen Mathematiker des 19.Jahrhunderts. [1822–1900])
Drei gleichartige Schränke haben jeweils zwei Schubladen.
In jeder Schublade befindet sich eine Münze.
Der eine Schrank enthält zwei Goldmünzen, der zweite Schrank zwei Silbermünzen und der dritte Schrank je eine Gold- und Silbermünze.
Ein Schrank wird zufällig gewählt und eine der Schubladen aufgezogen.
In ihr liegt eine Goldmünze.
Berechnen Sie die Wahrscheinlichkeit, dass auch die zweite Münze in diesem Schrank aus Gold ist.
|
  
    
 
|
|
 Aufgabe W6: Grüne und SUV Aufgabe W6: Grüne und SUV |
|
In der „Frankfurter Allgemeinen Sonntagszeitung (F.A.S.) vom 16. Mai 2021 wird unter der Überschrift „Die Liebe der Grünen zum SUV“ berichtet, dass Anhänger der Partei Bündnis90/Die Grünen mehr als Anhänger anderer Parteien einen SUV fahren würden. Grundlage des Berichts sind die bisher unveröffentlichten Ergebnisse einer Befragung des Marktforschungs- und Beratungsunternehmens puls von 1.042 Personen, die in den nächsten sechs Monaten die Anschaffung eines Autos planen oder in den vergangenen zwölf Monaten ein Auto gekauft haben. In dieser Gruppe fahren Anhängerinnen und Anhänger der Partei Bündnis 90/Die Grünen am häufigsten einen SUV (16,3 Prozent), gefolgt von Wählerinnen und Wählern der SPD (16,0 Prozent), der AfD (15,9 Prozent), der CDU/CSU (15,6 Prozent), der FDP (13,4 Prozent) und der Linken (7,7 Prozent). Die F.A.S. folgert aus diesen Ergebnissen: „Jeder sechste Grünen-Sympathisant hat laut der Puls-Studie einen Geländewagen vor der Tür stehen“.
Aus: Unstatistik des Monats, 28.5.2021
- Überlegen Sie, wie die Auswahl der Befragten erfolgt ist und wie die Fragen der Umfrage gelautet haben könnten.
- Prüfen Sie, ob der angegebene Prozentsatz für die Grünen in etwa zur Angabe im letzten Satz passt.
- Zeigen Sie an den nachfolgenden Beispielen, dass die bedingten Wahrscheinlichkeiten nicht durcheinander geworfen werden dürfen:
- Beispiel 1: 2017 gab es bei der Bundestagswahl 46 515 492 gültige Stimmen, die Anzahl der SUV lag Anfang 2021 bei rund 4,3 Mio.. Nehmen Sie an, dass es unter den SUV-Fahrern 75,4% Wähler (zufällig die Wahlbeteiligung 2017) gab.
- Formulieren Sie diese Annahme als bedingte Wahrscheinlichkeit.
- Drehen Sie nun die bedingte Wahrscheinlichkeit um, d.h. vertausche das vorausgesetzte Ereignis mit dem Folgeereignis. Formulieren Sie die Aussage als bedingte Wahrscheinlichkeit.
- Zeigen Sie die Unzulässigkeit des Vertauschens, indem Sie die daraus resultierende Zahl der SUV-Fahrer berechnen.
- Formulieren Sie den Generalfehler im Umgang mit bedingten Wahrscheinlichkeiten, allgemein und an dem Artikel oben.
- Beispiel 2: 2017 gab es 12 447 656 CDU-Wähler. Nehmen Sie an, dass es unter den befragten SUV-Fahrern 50 % CDU-Wähler gab.
Zeigen Sie an dem Beispiel erneut die Unzulässigkeit der Umkehrung, die im Artikel vorgenommen wurde.
-
Beispiel 3: Von den Sportunfällen bei Männern passieren rund 60 % beim Fußball. Daraus wird häufig geschlossen, dass der Fußball die gefährlichste Sportart ist. Notieren Sie dazu die bedingten Wahrscheinlichkeiten und erläutern Sie den Fehler.
-
Beispiel 4: Nehmen Sie an, dass 90 % aller sport-treibenden Männer „Kopfstand-Yoga“ als Sport ausüben. Wenn in dem Sport genauso viele Unfälle passieren wie bei den anderen Sportarten, können schnell Fehlurteile passieren. Benennen und erläuteren Sie sie.
- Zeigen Sie, dass die Auswahl der Befragten zu Fehlern führen kann:
- Sehen Sie sich die Auswahl der Befragten in dem Bericht der F.A.S. an. Erläutern Sie, inwiefern relevante Gruppen nicht erfasst werden, wenn man zuverlässige Aussagen zu Autonutzung und Parteienpräferenz machen will. Nennen Sie einige Gruppen.
- Ein weiteres Beispiel: Männer verdienen im Durchschnitt mehr als Frauen. Aber selbst wenn sie den gleichen Stundenlohn hätten, kann es deutliche Unterschiede geben. Löhne beziehen nämlich nur Beschäftigte ein. Erläutern Sie auch an diesem Beispiel die Problematik der Befragten-Auswahl.
Achtung:
In den Aufgabenteilen c. und d. ist mit „SUV-Fahrern“ immer gemeint: Personen, die in der Umfrage angaben, dass sie in den nächsten sechs Monaten die Anschaffung eines SUV planen oder in den vergangenen zwölf Monaten ein SUV gekauft haben.
|
 Bild von Sismadi Pujiantoro auf Pixabay Bild von Sismadi Pujiantoro auf Pixabay |
©2024 NET-SCHULBUCH.DE



 ELISA
ELISA





