Druckversion vom 27.07.2024 08:37 Uhr
Startseite Einführungsphase Stochastik Zufallsprozesse
Zufallsprozesse
| Grundlagen
In diesem Kapitel werden die Grundkenntnisse aus dem Unterricht in der Sekundarstufe I wiederholt, aufgearbeitet und neu gewichtet. |
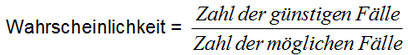 |
|
|
In Alltagssituationen statistische Wahrscheinlichkeiten Im alltäglichen Umfeld spielen statistische Wahrscheinlichkeiten bisher oft eine Rolle, wenn es heißt: |
|
|
|
 |
|
| Simulation von Zufallsexperimenten
Es gibt "vertrackte" Situationen, in denen man sich leicht verschätzt. Dann helfen oft Simulationen, um die hinter dem Experiment verborgenen Wahrscheinlichkeiten anzunähern. |
 |
|
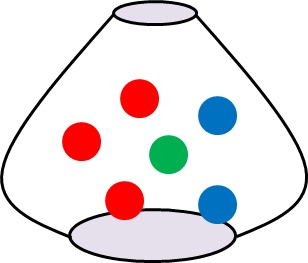
| Urnenmodelle
Zur systematischen Analyse von Zufallsversuchen werden Urnenmodelle genutzt, die zum Vergleich mit dem Experiment herangezogen werden. |
 |
|
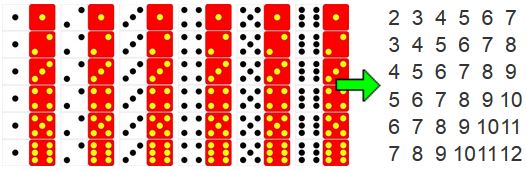
| Zufallsgröße
Der zentrale Begriff Zufallsgröße wird definiert und an Beispielen erklärt. |
 |
|
| Erwartungswert
Der zentrale Begriff Erwartungswert wird definiert und in Aufgabenstellungen vertieft. |
E(X) = a1p1 + a2p2 + ... + ampm | |
| Dunkelfeldforschung (optional)
Haben Sie bei der Klausur gemogelt? Haben Sie einmal etwas gestohlen? Wenn man Menschen zu sozial unerwünschten Verhaltensweisen befragt, kann man davon ausgehen, dass viele nicht wahrheitsgemäß antworten, Bei der Randomized-Response-Technik - die auf den folgenden Seiten erklärt wird - sorgt eine Zufallsverschlüsselung dafür, dass die Wahrheit ans Licht kommt. |
 |


