Quelle: https://nwm2.net-schulbuch.de/index.phpDruckversion vom 25.09.2023 18:25 Uhr
Startseite Qualifikationsphase Analytische Geometrie
Lineare Algebra Grundlagen
Analytische Geometrie - Grundlagen
Die Schulgeometrie befasst sich mit der Anwendung von mathematischen Verfahren und Techniken zur Messung und Beschreibung von Objekten, die durch feste Orte (Punkte) in einem zwei- oder dreidimensionalen Raum definiert sind.
Viele dieser mathematischen Grundlagen aus den Vorjahren werden vorausgesetzt. So zum Beispiel:
| gleichseitiges~, gleichschenkliges~, rechtwinkliges~ / Umfang, Fläche / Höhe, Seitenhalbierende, Winkelhalbierende / Schwerpunkt / Winkelsumme |
|
| Quadrat, Rechteck, Raute, Trapez / Umfang, Fläche / Diagonale |
|
| Würfel, Quader / Volumen, Oberfläche / Raumdiagonale |
|
| Umkehrung des Satzes des Pythagoras, Höhensatz, Satz des Thales |
|
| Sinus, Kosinus, Tangens, Bogenmaß |
Stichworte dazu
| Punkte im Raum
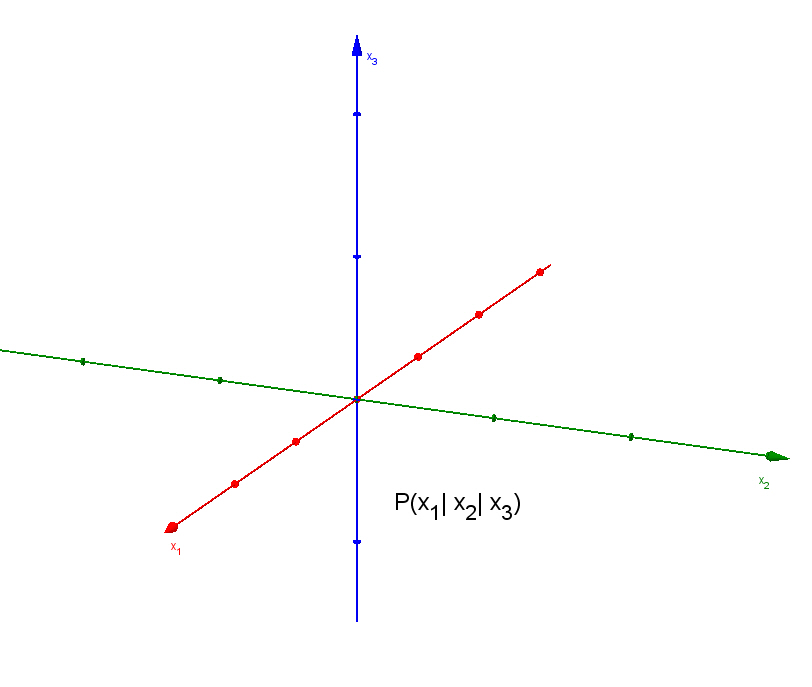
In der Geometrie der zwei- und dreidimensionalen Räume heißt der Ursprung üblicherweise `O`(origin) und erhält im Standardkoordinatensystem die Werte `(0|0|0)`. Es hat sich das kartesische Koordinatensystem zur Darstellung, Rechnung und Beschreibung bewährt, in dem die Achsen senkrecht zueinander stehen.Normalerweise erfolgt eine Bezeichnung wie in der nebenstehenden Skizze. Ausführliche Informationen dazu finden Sie in der Einführungsphase |
|
|
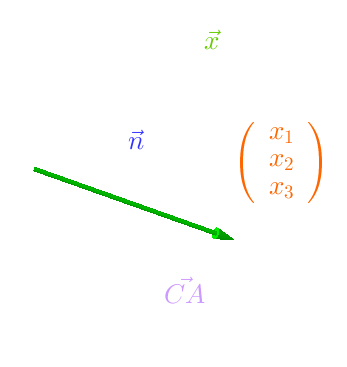
Gerade Bewegungen im Raum sind durch einen Startpunkt und einen Endpunkt festgelegt. Im Koordinatensystems können diese Bewegungen auch als als Verschiebung betrachtet werden, deren Richtung und Länge durch die Koordinaten x1, x2, x3 bestimmt sind. Man bezeichnet diese Bewegungsklasse als Vektor und schreibt sie im Normalfall als untereinander gestelltes Zahlentripel im dreidimensionalen kartesischen Koordinatensystem .Ausführliche Informationen dazu finden Sie in der Einführungsphase |
|
