Druckversion vom 15.05.2024 08:10 Uhr
Startseite Einführungsphase Funktionen & Analysis Funktionen Winkelfunktionen
Winkelfunktionen - Lehrtext
|
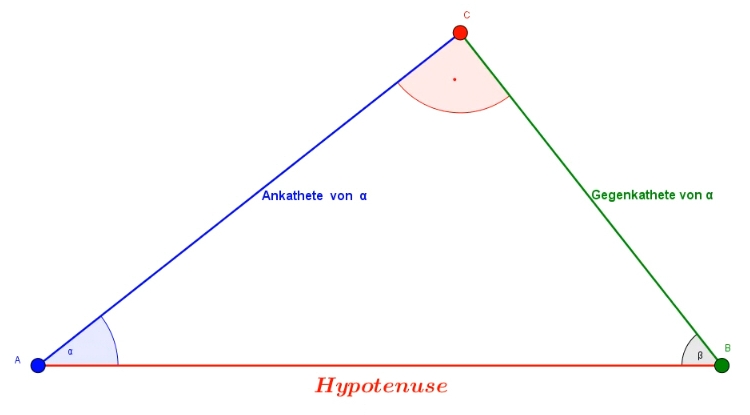
In jedem rechtwinkligen Dreieck gilt für die beiden Winkel an der Hypotenuse:
Sinus eines Winkels = `\color{green}{"Gegenkathete des Winkels"}/\color{red}{"Hypotenuse"}` Kosinus eines Winkels = `\color{blue}{"Ankathete des Winkels"}/\color{red}{"Hypotenuse"}` Tangens eines Winkels = `\color{green}{"Gegenkathete des Winkels"}/\color{blue}{"Ankathete des Winkels"}`
Die entsprechenden Funktionen im Taschenrechner kann man nutzen, um gesuchte Dreiecksseiten bzw. Winkel zu bestimmen. |
 |
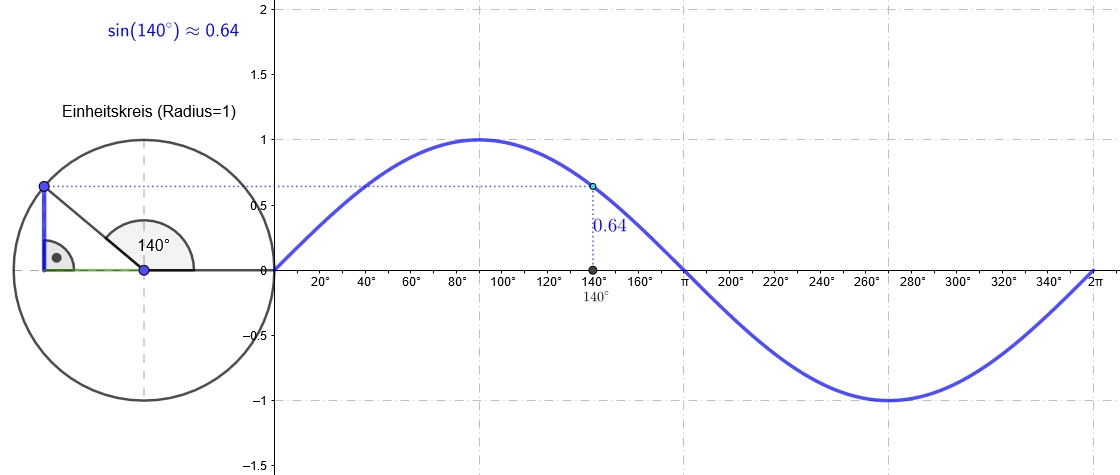
Wenn Sie diesen Graphen der sinus-Funktion genau betrachten, so fällt Ihnen sicher auf, dass die Achseneinteilungen auf der x-Achse und auf der y-Achse nicht gleich sind:
Die Funktionswerte auf der y-Achse liegen zwischen `-1` und `1`, die Werte auf der x-Achse zwischen `0^@` [Grad] und `90^@` [Grad].
Eine Vereinheitlichung der Einteilungen ist ein Grund für die Einführung des Bogenmaßes.
Geometrischer Bezug:
"Das Bogenmaß entsteht durch das Abrollen des Einheitskreises auf der x - Achse."
|
|
So haben Sie den Bogen raus!
|
Für den Umfang `U` eines Keises gilt: `U = 2*pi*r`.
Für einen Einheitkreis gilt `r = 1`, also ist `U = 2pi`.
Jeder im Einheitskreis eingebettete Winkel (s.o.) verfügt über einen Abschnitt des Kreisrandes.
Damit gilt für beliebige Winkel `alpha` und für das zugehörige Bogenmaß (`hat =` Länge des Kreisrandabschnitts) `x:`
`x/(2*pi) = alpha/360`.
Die Umrechnung eines Bogenmaßes in Grad erfolgt also nach folgender Formel:
`"Grad" = "Bogenmaß" *180/π`
Umgekehrt gilt:
`"Bogenmaß" = "Grad"*pi/180`
Im Englischen heißt das Bogenmaß radian, daher finden Sie häufig die Abkürzung RAD oder R auf Ihrem TR.
Hinweise zur Nutzung des Taschenrechners:
Bei Verwendung von trigonometrischen Funktionen muss der Taschenrechner zuvor
auf Bogenmaß oder Gradmaß eingestellt werden.
Schauen Sie dazu in die Bedienungsanleitung Ihres Taschenrechners.
Bei einigen Rechnern wählen Sie (evtl. shift-) MODE oder die DRG-Taste.
Beachten Sie auch die Anzeigen im Display des Taschenrechners.
|
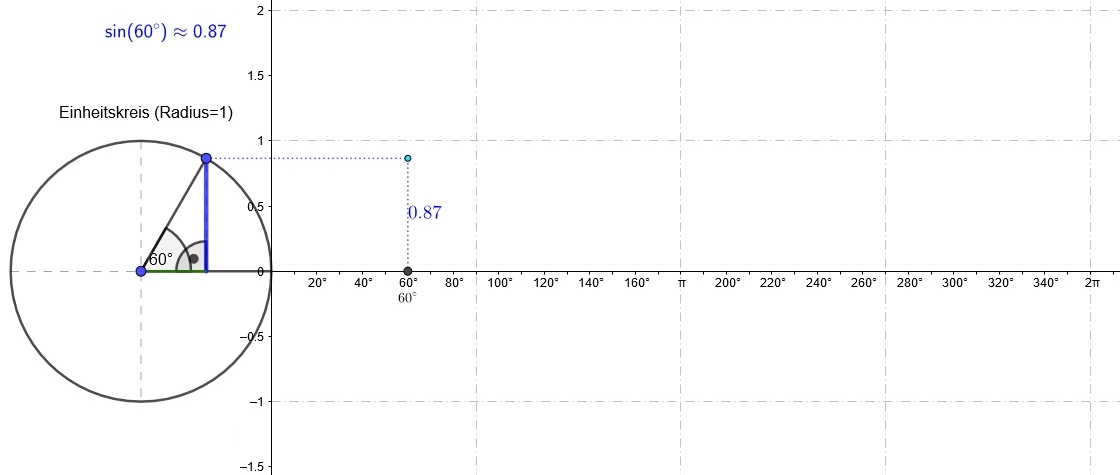
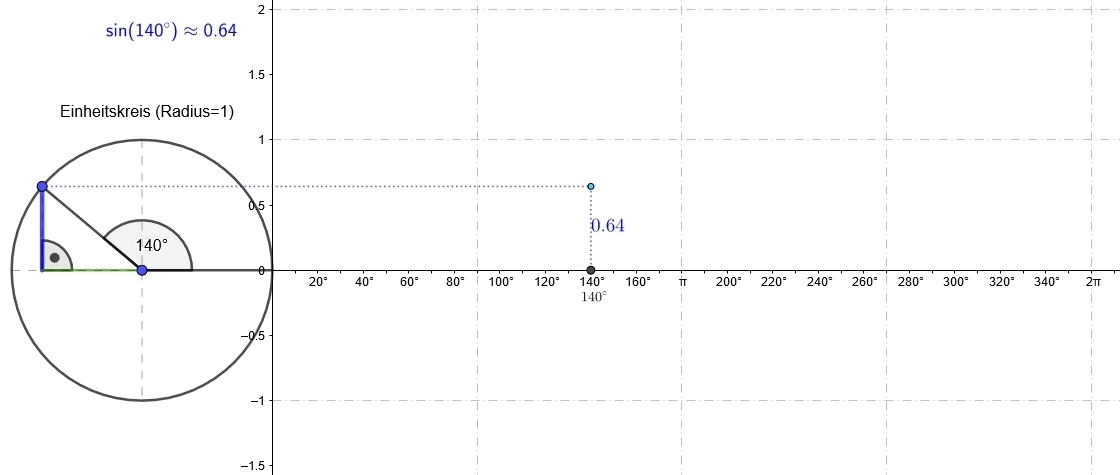
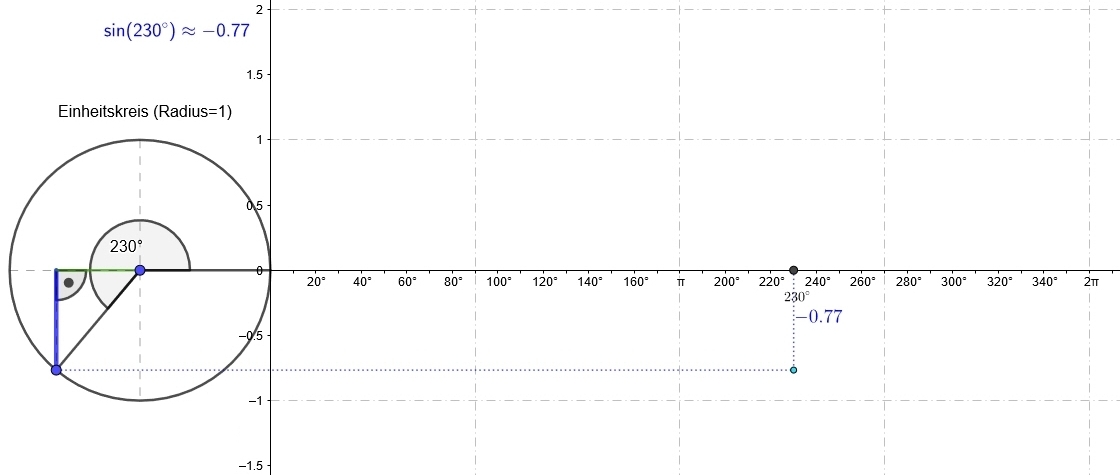
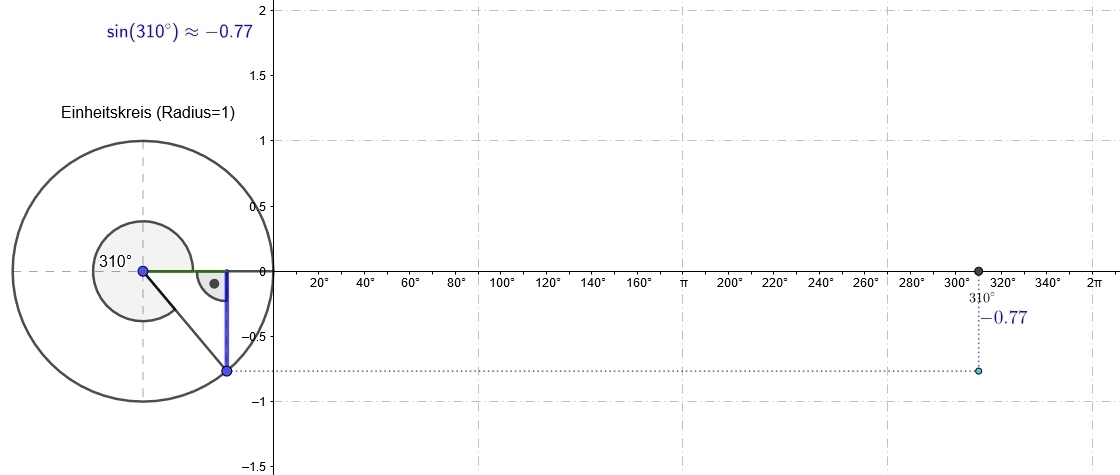
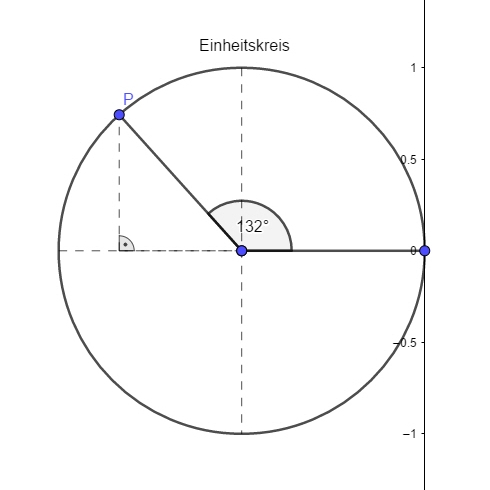
Ein im Einheitskreis (Kreis mit `r = 1`) eingebetteter Winkel `alpha` dient als Grundlage der Definition der Werte der Winkelfunktionen Sinus, Kosinus und Tangens.
Der Scheitelpunkt des Winkels ist der Kreismittelpunkt `(0 | 0)` in einem eigenen Koordinatensystem.
Ein Schenkel des Winkels wird durch den Punkt `(1 | 0)` auf dem Kreisrand festgelegt.
Der zweite Schenkel wird durch einen weiteren "freien" Punkt `P` mit den Koordinaten `(x | y)` auf dem Kreisrand bestimmt.
Die "Drehrichtung" des Schenkels wird mathematisch positiv - "gegen die Uhr" festgelegt.
Dann gelten die folgende Definitionen:
|
 |
|
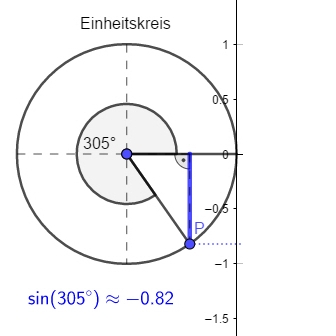
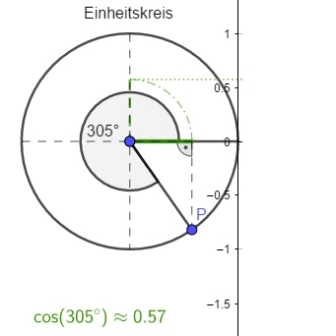
| Der Sinus des Winkels `alpha [sin(alpha) ]` ist der y-Wert von `P`. | Der Kosinus des Winkels `alpha [cos(alpha) ]` ist der x-Wert von `P`. |
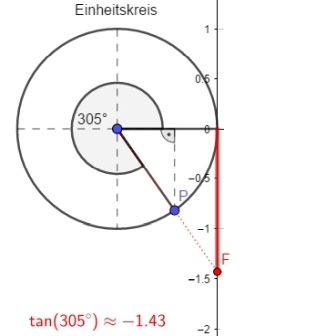
Die Gerade durch `P` und den Mittelpunkt des Kreises schneidet die Senkrechte zum festen Schenkel von `alpha` in `(1 | 0)` im Punkt `F`.
Der Tangens des Winkels `alpha [tan(alpha) ]` ist der y-Wert von `F`.
|
 |
 |
 |
|
Bei vielen Aufgabenstellungen ist es notwendig, zu bekannten Werten einer Winkelfunktion den zugehörigen Winkel zu ermitteln.
Diese Berechnungen erfolgen mit den jeweiligen Umkehrfunktionen (Arkusfunktionen) der Winkelfunktionen.
Sie tragen die Bezeichnungen: `arcsin` oder `sin^-1` `arccos` oder `cos^-1` `arctan` oder `tan^-1` .
Die Umkehrfunktionen existieren nur in Bereichen, in denen die Funktionen streng monoton sind. Daher wird bei der Funktion `sin^-1` für den Definitionsbereich `[-1 ; 1]` der Wertebereich `[-pi/2 ; pi/2] "/" [-90^@;+90^@]` im TR gewählt.
Für `cos^-1` ist analog dazu für den Definitionsbereich `[-1 ; +1]` der Wertebereich im Normalfall auf `[0 ; pi] "/" [0^@ ; 180^@]` beschränkt.
Bei `tan^-1` mit dem Definitionsbereich `[-oo ; + oo]` wird der Wertebereich `[- pi/2 ; pi/2] "/" [-90^@ ; +90^@]` gewählt.
Beispiele: `sin alpha = 0.3 rArr alpha = sin^-1(0.3) ~~ 17.46^@ ~~ 0.30` (Bogenmaß) `cos alpha = 0.3 rArr alpha = cos^-1(0.3) ~~ 72.54^@ ~~ 1.27` (Bogenmaß) `tan alpha = 0.3 rArr alpha = tan^-1(0.3) ~~ 16.70^@ ~~ 0.29` (Bogenmaß) Weitere Werte finden sie in den Tabellen weiter unten. |
Es gilt: `sin (alpha) = cos (90^@ - alpha)` bzw. `cos(alpha) = sin (90^@ - alpha)`
- "Sinus und Kosinus sind um `90^@` gegeneinander verschoben."
Die Sinusfunktion und die Kosinusfunktion sind für alle reellen Zahlen `x` (Bogenmaß!) `(x in RR)` definiert.
Die Werte liegen im Bereich von `-1` bis `+1`.
Es gilt z.B.:
`sin (x + 2pi) = sin(x)` und `cos(x + 2pi) = cos(x)`.
Man sagt dazu: Die Sinusfunktion und die Kosinusfunktion sind periodisch mit der Periode `2pi` `(hat = 360^@)`.
`sin(-x) = - sin(x)`, d.h. die Sinusfunktion ist punktsymmetrisch zum Ursprung des Koordinatensystems.
`cos(-x) = cos(x)`, d.h. die Kosinusfunktion ist achsensymmetrisch zur y-Achse.
`cos(x) = sin(x + 1/2 pi)`
`tan (alpha) = sin(alpha)/cos(alpha)`
| Winkel in Grad | sin | cos | tan |
|---|---|---|---|
| 0° | `1/2*sqrt 0` = 0 | `1/2*sqrt 4` = 1 | 0 |
| 30° | `1/2*sqrt 1` = 0,5 | `1/2*sqrt 3` ≈ 0,866 | `1/3*sqrt 3` ≈ 0,577 |
| 45° | `1/2*sqrt 2` ≈ 0,707 | `1/2*sqrt 2` ≈ 0,707 | 1 |
| 60° | `1/2*sqrt 3` ≈ 0,866 | `1/2*sqrt 1` = 0,5 | `sqrt 3` ≈ 1,732 |
| 90° | `1/2*sqrt 4` = 1 | `1/2*sqrt 0` = 0 | nicht definiert / ±∞ |
| 120° | `1/2*sqrt 3` ≈ 0,866 | `-1/2*sqrt 1` = -0,5 | `-sqrt 3` ≈ -1,732 |
| 135° | `1/2*sqrt 2` ≈ 0,707 | `-1/2*sqrt 2` ≈ -0,707 | -1 |
| 150° | `1/2*sqrt 1` = 0,5 | `-1/2*sqrt 3` ≈ -0,866 | `-1/3*sqrt 3` ≈ -0,577 |
| 180° | `1/2*sqrt 0` = 0 | `-1/2*sqrt 4` = -1 | 0 |
| 210° | `-1/2*sqrt 1` = -0,5 | `-1/2*sqrt 3` ≈ -0,866 | `1/3*sqrt 3` ≈ 0,577 |
| 225° | `-1/2*sqrt 2` ≈ -0,707 | `-1/2*sqrt 2` ≈ -0,707 | 1 |
| 250° | `-1/2*sqrt 3` ≈ -0,866 | `-1/2*sqrt 1` = -0,5 | `sqrt 3` ≈ 1,732 |
| 270° | `-1/2*sqrt 4` = -1 | `1/2*sqrt 0` = 0 | nicht definiert / ±∞ |
| 300° | `-1/2*sqrt 3` ≈ -0,866 | `1/2*sqrt 1` = 0,5 | `-sqrt 3` ≈ -1,732 |
| 315° | `-1/2*sqrt 2` ≈ -0,707 | `1/2*sqrt 2` ≈ 0,707 | -1 |
| 330° | `-1/2*sqrt 1` = -0,5 | `1/2*sqrt 3` ≈ 0,866 | `-1/3*sqrt 3` ≈ -0,577 |
| 360° | `1/2*sqrt 0` = 0 | `1/2*sqrt 4` = 1 | 0 |
| Winkel in Bogenmaß | sin | cos | tan |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| `pi/6 hat =` 30° | 0,5 | ≈ 0,866 | ≈ 0,577 |
| `pi/4 hat =` 45°` | ≈ 0,707 | ≈ 0,707 | 1 |
| `pi/3 hat =` 60°` | ≈ 0,866 | 0,5 | ≈ 1,732 |
| `pi/2 hat =` 90°` | 1 | 0 | nicht definiert / ±∞ |
| `pi hat =` 180°` | 0 | -1 | 0 |
| 0,5 ≈ 28,648° | ≈ 0,479 | ≈ 0,878 | ≈ 0,546 |
| 1 ≈ 57,296° | ≈ 0,841 | ≈ 0,540 | ≈ 1,557 |


 Bogenmaß am Einheitskreis
Bogenmaß am Einheitskreis