Druckversion vom 27.07.2024 06:22 Uhr
Startseite Qualifikationsphase Analytische Geom., Lineare Alg
Analytische Geometrie und Lineare Algebra
| Grundlagen Einige grundlegenden Inhalte der Analytischen Geometrie aus der Einführungsphase werden noch einmal kurz dargestellt. Zur Ausführlichen Bearbeitung verweisen wir auf die Ausführungen in der Einführungsphase. (net-code: ac_index) |
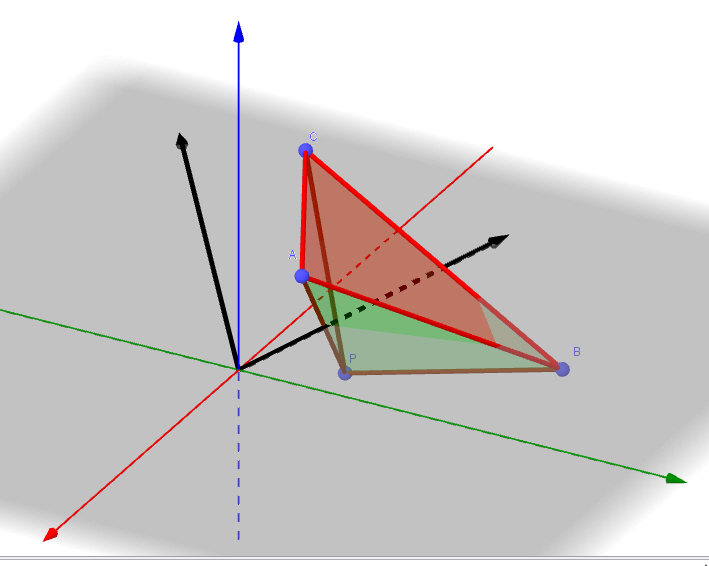 |
|
Grundlagen (Alternative am Beispiel der Spidercam) Einige Inhalte der Analytischen Geometrie aus der Einführungsphase werden noch einmal kurz am Beispiel der Spidercam dargestellt. Zur Ausführlichen Bearbeitung verweisen wir auf die Ausführungen in der Einführungsphase |
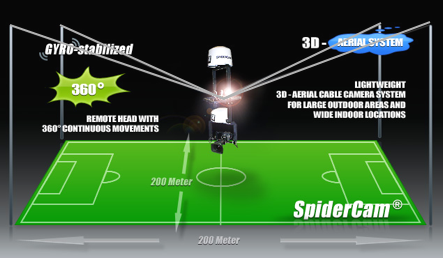 |
| Lineare Gleichungssysteme
Es wird an ein Lösungsverfahren für lineare Gleichungssysteme erinnert, das Sie aus der Mittelstufe kennen. Dann lernen Sie das universelle Gauss-Verfahren kennen, mit dem Sie auch große lineare Gleichungssysteme mit elementaren Umformungen lösen können. Danach wenden Sie das Gelernte an und in der Zusammenfassung werden exemplarisch alle Lösungsmöglichkeiten aufgezeigt. |
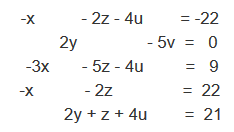 |
| Geraden
"The vector equation of the line through points A and B is given by If a is vector OA and b is vector OB, then the equation of the line can be written: So meint es Wikipedia! [https://en.wikipedia.org/wiki/Line_(geometry)] Hier erfahren Sie, wie es in diesem Buch gemeint ist! Ab dem Schuljahr 2023/24 gehört das Kapitel "Geraden" in NRW zum Lehrplaninhalt in der Einführungsphase.
Daher wird das identische Kapitel ebenfalls in der EF gelistet. (net-code: ac_) |
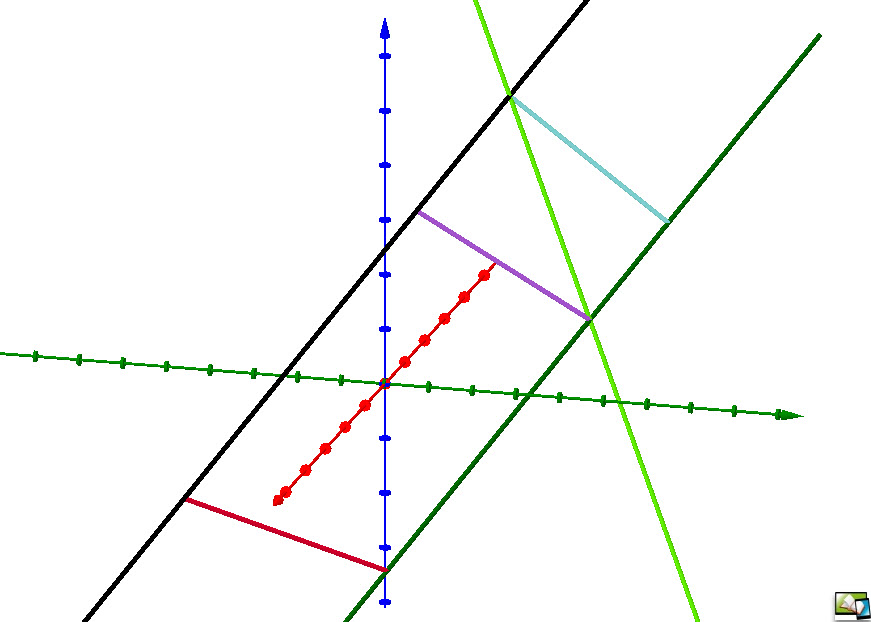 |
| Skalarprodukt
Het scalaire product van twee vectoren is 0 als de vectoren loodrecht op elkaar staan. The scalar product of two vectors is 0 if the vectors are perpendicular to each other. Le produit scalaire de deux vecteurs est égal à 0 si les vecteurs sont perpendiculaires entre eux. El producto escalar de dos vectores es 0 si los vectores son perpendiculares entre sí. Il prodotto scalare di due vettori è 0 se i vettori sono perpendicolari tra loro. |
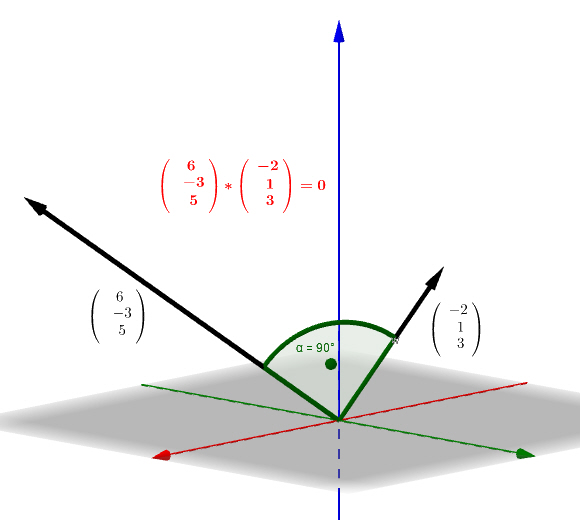 |
| Ebenen
Hier erfahren Sie endlich, warum ein dreibeiniger Hocker nie wackelt! Mit der Drei-Punke-Form und der Parameterform der Ebenengleichung werden Ebenen im Raum charakterisiert. Vertiefend wird auch die Koordinatenform behandelt. |
 |
| LK: Erweiterungen
In diesem - vorwiegend für Leistungskurse konzipierten Teil - werden folgende Inhalte behandelt:
|
 |
| Matrizen (optional) In diesem Teil werden zunächst die Grundlagen der Matrizenrechnung erarbeitet. Mithilfe von Übergangsmatrizen und stochastischen Matrizen werden Austauschprozesse und Populationsentwicklungen behandelt. Abbildungsmatrizen sind ein geeignetes Mittel, um z.B. Kongruenzabbildungen genauer zu untersuchen.
|
 |
| Komplexe Aufgaben
Neben mehreren anspruchsvolleren Aufgaben finden Sie hier eine Sammlung von Abituraufgaben mit ausführlichen Lösungen. Zum Teil werden die Lösungen in einem Video vorgerechnet. Kunst und Bewegung in der dreidimensionalen Welt fordern die Vektorgeometrie! |
 |
 Hinweis auf Materialien zu diesem Thema aus der
Hinweis auf Materialien zu diesem Thema aus derMathematik-Unterrichts-Einheiten-Datei des MUED e.V.

Das vom MUED e.V. in zwei Größen vertriebene 3D-Modell und seine Ergänzungen erlauben eine experimentelle und anschauliche Darstellung der Zusammenhänge bei der Spidercam




 Hinweis
Hinweis