Quelle: https://nwm2.net-schulbuch.de/index.phpDruckversion vom 29.04.2024 04:54 Uhr
Startseite Qualifikationsphase Analysis LK: Funktionenscharen
LK: Funktionenscharen - Lehrtext
Die Bezeichnung der Schar erfolgt mit dem zusätzlichen Parameter als Index z.B. `f_a(x)`
Die Funktionseigenschaften (Extrempunkte / Nullstellen / Verhalten im Unendlichen / ...) hängen neben der Grundstruktur dann entscheidend von dem Parameter ab.
|
Beispiel 1:
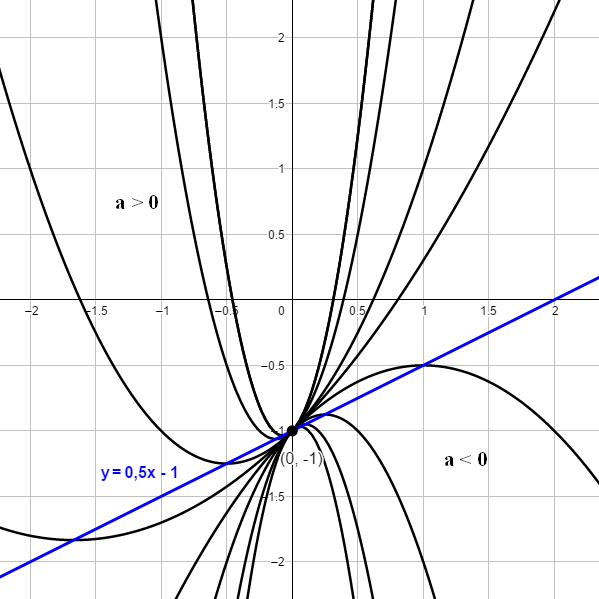
`f_a` mit `f_a(x) = ax^2 + x - 1 a in RR` Für a≠0 handelt es sich um quadratische Parabeln. [`f_0(x) = x - 1` ist eine Gerade mit der Steigung 1 durch `(0| -1)`.]
Alle Graphen verlaufen durch den Punkt `( 0 | -1 )`.
Für a>0 sind die Parabeln nach oben, für a < 0 nach unten geöffnet. Die Scheitelpunkte sind: `S_a = ( - 1/(2a) | -(1 + 1/(4a)))`. Diese Scheitelpunkte liegen alle auf der Geraden mit der Gleichung `y=0,5x-1`. `f_a(0) = - 1`
Umformung in die Scheitelpunktform: `f_a(x) = ax^2 + x - 1` `= a*( x^2 + 1/ax) - 1` `= a*(x^2 + 1/ax + 1/(4a^2)) - 1/(4a) - 1` `= a*( x + 1/(2a))^2 - (1 + 1/(4a))` `rArr S_a = ( - 1/(2a) | -(1 + 1/(4a)))` oder `f_a^'(x) = 2ax + 1` `f_a^'(x) = 0 hArr x = - 1/(2a)` Da `f_a` quadratische Parabeln sind, ist das die Stelle des jeweiligen lokalen Extremums mit `f_a(- 1/(2a)) = a*(- 1/(2a))^2 + (- 1/(2a)) - 1` `= 1/(4a) - 1/(2a) - 1 = - (1 + 1/(4a))` . Für die Scheitelpunkte gilt: `x = - 1/(2a) rArr a = - 1/(2x)` `y = -(1 + 1/(4a))` `= - ( 1 + 1/(4*(- 1/(2x))))` `= - (1 - x/2) = 0.5x - 1`
|
 |
|
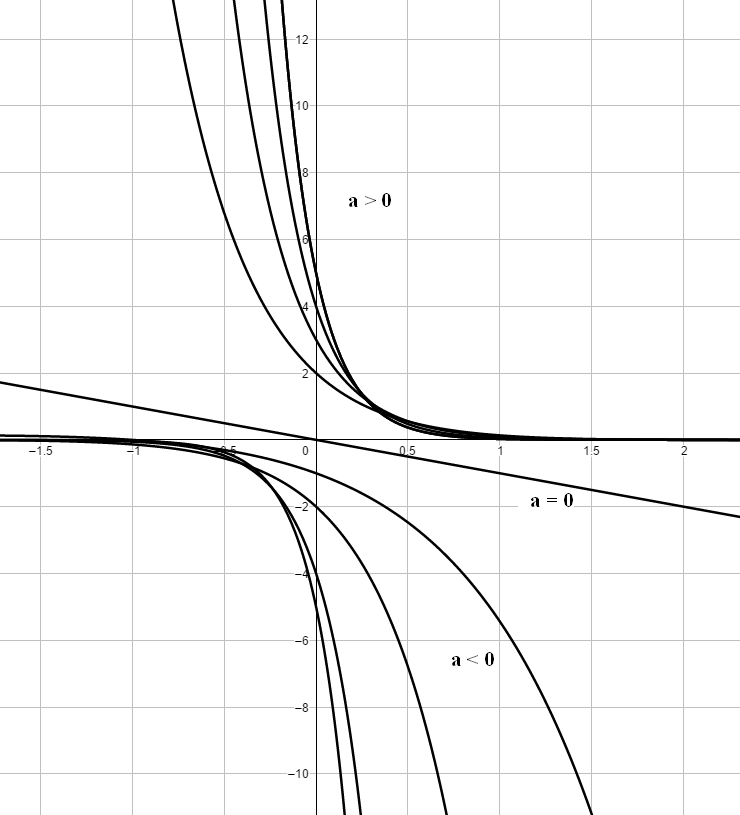
Beispiel 2: `f_a` mit `f_a(x) = (a - x) * e^(-ax) a in RR ` Für a = 0 handelt es sich um die Gerade y = -x. Die Graphen dieser Produktfunktionen aus einem Exponentialfaktor und einem ganzrationalen Faktor bilden eine Kurvenschar, deren Verlauf entscheidend vom Vorzeichen des Parameters a abhängt. Eigenschaften: Nullstelle: `x = a` lokale/relative Extremstelle: `x = a + 1/a` Wendestelle: `x = a + 2/a` Grenzwerte: `a > 0 rArr` `lim_(x->+oo)f_a(x) = uarr 0` und `lim_(x->-oo)f_a(x) = +oo` `a < 0 rArr` `lim_(x->+oo)f_a(x) = -oo` und `lim_(x->-oo)f_a(x) = darr 0` Sei `a != 0` Aufgrund der Eigenschaft der e-Funktion [ex > 0 für alle x] haben alle Graphen wegen des ersten Faktors genau eine Nullstelle bei x = a. Mit der linearen Kettenregel und der Produktregel gilt:`f_a^'(x) = -e^(-ax) + (a-x)*(-a)*e^(-ax)` `= (-1 - a^2 + ax)*e^(-ax)` `rArr f_a^'(x) = 0 hArr x = (a^2+1)/a = a + 1/a` `f_a^('')(x) = a*e^(-ax) + (-1 - a^2 + ax)*(-a)*e^(-ax)` `= (a + a + a^3 - a^2x)*e^(-ax)` `= (2a + a^3 - a^2x)e^(-ax)` `rArr f_a^('')((a^2+1)/a) = ( 2a + a^3 - (a^2*(a^2 + 1))/a)*e^(-a*(a^2+1)/a))` `= (2a + a^3 - a^3 - a)e^(-a^2-1)` `= a*e^(-a^2-1) [(> 0 "für" a>0),(< 0 "für" a<0)]` `rArr "lokaler" [( "TP für" a>0),( "HP für" a<0)]` mit `f_a((a^2+1)/a) = (a -(a^2+1)/a)*e^(-a^2-1) = - 1/a*e^(-a^2-1)` `f_a^('')(x) = 0 hArr x = (2a + a^3)/a^2 = a + 2/a` Aufgrund der lokalen Extrema und der Grenzwerte handelt es sich um Wendepunkte mit `f_a(2/a+a) = - 2/a*e^(2-a^2)` |
 |
|
`f_a(x) = a^2x^3 - a^3x^2 + 2a =>` `f_a^'(x) = 3a^2x^2 - 2a^3x =>` `f_a^('')(x) = 6a^2x - 2a^3 => ` `f_a^(''')(x) = 6a^2` |
`f_a(x) = (ax^2 - a)*e^(-a^2x) rArr` `f_a^'(x) = 2ax*e^(-a^2x) + (ax^2 - a)*(-a^2)*e^(-a^2x)` `= (-a^3x^2 + 2ax + a^3)*e^(-a^2x)` `f_a^('')(x) = (-2a^3x + 2a)*e^(-a^2x) + (-a^3x^2 + 2ax + a^3)*(-a^2)*e^(-a^2x)` `= (-2a^3x + 2a + a^5x^2 - 2a^3x - a^5)*e^(-a^2x)` `= ( a^5x^2 - 4a^3x + 2a - a^5)*e^(-a^2x)` |
|
Bei der Untersuchung von Funktionenscharen müssen oft Fallunterscheidungen gemacht werden um die Auswirkungen des Parameters beschreiben zu können.
Diese Fallunterscheidung wird auch Klassifizierung genannt.
z.B. `f_a(x) = ax^2 + a^2`
1.Fall: `a > 0` : nach oben geöffnete Parabelschar ohne Nullstellen
2.Fall: `a < 0`: nach unten geöffnete Parabelschar mit den beiden Nullstellen `+- sqrt(-a)`
3.Fall: `a=0` `f_0(x) = 0 `
Scheitelpunkt jeweils `S=(0|a^2)`
|