×
Net-Mathebuch
Sekundarstufe 2
 

Seite: bbg_aufgaben2
Diese Seite wurde aktualisiert am 03.10.2023

LOGIN
Benutzer:
Passwort:
 
Geogebra-

Chat

Quelle: https://nwm2.net-schulbuch.de/index.php
Druckversion vom 29.04.2024 06:08 Uhr
Startseite Qualifikationsphase Analysis LK: Funktionenscharen
Startseite Qualifikationsphase Analysis LK: Funktionenscharen Diese Seite wurde aktualisiert am 03.10.2023

LK: Funktionenscharen - Aufgaben 2

 

Aufgabe I1  

Eine an ihren Enden frei aufgehängte nicht dehnbare Kette, die nur von der Schwerkraft beeinflusst ist, bildet den Graphen einer sogenannten Kettenlinie.

[Wenn Sie 'mal in der Gegend sind: Das kleine Örtchen Moustiers Sainte-Marie oberhalb des Lac de St.Croix in der Provence verfügt über eine über 200m lange Metallkette an der an vergoldeter Stern aufgehangen wurde.]

Diese Graphen werden von Funktionen der Funktionenschar `f_a(x) = a/2*(e^(x/a) + e^(-x/a))`  mit  `a !=0`  gebildet.

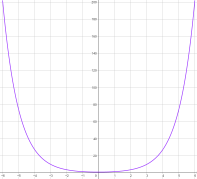
Für a = 1 bildet der Graph den sogenannten cosinus hyperbolicus.

cosh

Veranschaulichen Sie die Ergebnisse der folgenden Berechnungen für `f_-1`  und  `f_4` und nutzen Sie dabei das Definitionsintervall `[-4;+4]`.

  1. Untersuchen Sie die Funktionen auf Symmetrie und berechnen Sie Nullstellen und lokale/relative Extrema.
  2. Berechnen Sie die Größe der Fläche zwischen Kettenlinie und x-Achse in den Grenzen von -b bis b (b > 0) für beliebiges a.

    Beschreiben Sie den Zusammenhang zwischen der Flächenmaßzahl und dem Integral je nach Vorzeichen von a.

  3. Bei Rotation der Kettenlinie um die x-Achse entsteht ein Drehkörper, ein sogenanntes Katenoid.
    Berechnen Sie das Volumen des Katenoidabschnitts in den Grenzen von -b bis b (b > 0).

    Untersuchen Sie, ob das Vorzeichen von a Einfluss auf das Vorzeichen der Volumenmaßzahl hat.
    Prüfe Sie dafür die Berechnungsformel und speziell den Ergebnisterm.

Stern an der Kette über Moustiers!

Näheres zur Legende

 

 

Aufgabe I2  

Gegeben ist die reelle Funktionenschar  `f_a(x) = (a + ln x)/x`  mit `a in RR`.

Stellen Sie den Verlauf der Funktionsgraphen von `f_-1`,  `f_0`, `f_1` und `f_2` im Intervall `(0 ; 3]` parallel zur Aufgabenlösung mit Hilfe von GeoGebra oder Ihrem GTR dar.

  1. Untersuchen Sie das Verhalten der `f_a` am Rande des Definitionsbereiches.
  2. Untersuchen Sie die Funktionen auf Nullstellen, Extrema und Wendepunkte und zeigen Sie, dass jeweils genau eine Nullstelle und ein Extremwert existiert.
  3. Zeigen Sie durch Anwendung von Integrationsregeln, dass `F_a(x) = a*ln x + 1/2 ln^2 x` eine Stammfunktionsschar ist.
  4. Berechnen Sie die Fläche zwischen dem Funktionsgraphen von `f_1`und der x-Achse im Intervall `[ e^-1 ; 1]`.
  5. Zeigen Sie, dass die vom Graph und der x-Achse eingeschlossene Fläche für alle Funktionen zwischen Nullstelle und Extremwert konstant ist und geben Sie den Wert an.

 

Aufgabe I3  

Gegeben sei die Funktionenschar `f_a`  mit `f_a(x) =  (10x)/(x^2 + a^2)      a > 0`.

  1. Untersuchen Sie die Funktionen `f_a` auf Symmetrie, Polstellen und ihr Verhalten für große und kleine x-Werte.
  2. Bestimmen Sie Nullstellen, Extrem- und Wendepunkte.
  3. Zeichnen Sie mit Hilfe von GeoGebra oder Ihrem GTR die Graphen der Funktionen `f_1` und `f_2` und bestimmen Sie die besonderen Punkte mithilfe der Ergebnisse aus Teilaufgabe b..
  4. Zeigen Sie: Alle Funktionsgraphen haben einen gemeinsamen Punkt.
  5. Bestimmen Sie die Funktionsvorschriften für die Ortskurven der Extrempunkte und der Wendepunkte.
  6. Bestimmen Sie die Maßzahl der Fläche, die zwischen den Graphen von `f_1` und `f_2` liegt.
  7. Zeigen Sie, dass `int_-b^b f_a(x) dx = 0`.

 

 

Aufgabe W1  

In einer Keksfabrik wird täglich in  6-Stunden-Schichten produziert.

In der Einheit Tonnen/Stunde kann man die in jeder Schicht von den Teigmaschinen zum Zeitpunkt `0 <= x <= 6` (x in Stunden) momentan hergestellte Teigmenge mit der Funktionenschar

`f_a(x)  = e^(-ax)*(5x + 1)`   beschreiben. `a > 0`

Stellen Sie den Verlauf der Funktionsgraphen parallel zur Aufgabenlösung mit Hilfe von GeoGebra oder Ihrem GTR dar.

  1. Berechnen Sie den Zeitpunkt, an dem nach dieser Modellierung das absolute Maximum der Produktion in der Schicht erreicht wird. Bestimmen Sie den Wert für den Scharparameter a, so dass dieses Maximum nach genau einer Stunde erreicht wird.

  2. Berechnen Sie den Wert des Scharparameters a, so dass diese Modellierung für eine analoge Beschreibung aller aufeinanderfolgenden Arbeitsschichten genutzt werden könnte. Beschreiben Sie die Problematik des "Schichtübergangs" in dem Modell.

  3. Berechnen Sie durch Anwendung von Integrationsregeln eine Stammfunktionenschar der `f_a` und berechnen Sie den Term für die in einer Schicht hergestellte Teigmenge.
    Geben Sie die Gesamtteigmenget für das a aus Teilaufgabe b. exakt an.

 

Aufgabe W2  

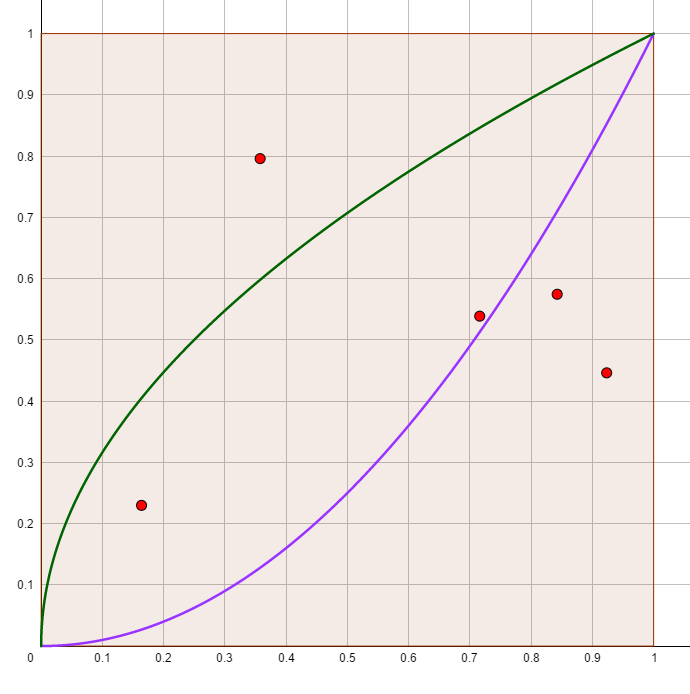
Die beiden Funktionsgraphen von `f(x) = x^2` und `g(x) = sqrt(x)` begrenzen das Trefferfeld innerhalb des 1x1-Quadrates einer Standard-Parabel-Dart-Scheibe in einem Spielautomaten. (s.Graphik)

Mit einem Zufallszahlengenerator werden dabei 5 Punkte in der 1x1-Fläche erzeugt.

Ein Mathematiker kam auf die Idee, die Parabel-Dart-Scheibe allgemeiner als ein Quadrat mit der Seitenlänge a `(a > 0) ` zu beschreiben.

Als begrenzende Funktionen wählte er `f_a(x) = 1/a x^2`  und `g_a(x) = sqrt(ax)`.

Die Zufallswerte für die Punktkoordinaten werden jeweils aus dem Intervall `[0;a]`  erzeugt.

  1. Berechnen Sie die Wahrscheinlichkeit für die Standard-Scheibe, bei einem "Wurf" einen Treffer zu erzielen, d.h. einen Punkt zu erhalten, der innerhalb der Fläche liegt.
  2. Berechnen Sie die Wahrscheinlichkeit, bei 5 gleichzeitigen "Würfen" des Automaten mindestens einen und höchstens drei Treffer zu erzielen.
  3. Zeigen Sie, dass die beiden genutzten Funktionenscharen im Definitionsbereich `[0;a]` folgende Eigenschaften haben:
    1. Die Graphen der Funktionen `f_a` und `g_a` haben genau zwei gemeinsame Punkte `(0|0)`  und `(a|a)`.
    2. Die Funktionen sind jeweils Umkehrfunktionen zueinander.
  4. Zeigen Sie, dass die Trefferwahrscheinlichkeit nicht von a abhängt.

 

Aufgabe W3  

In der Forschung zur Abwehr und Bekämpfung von ‚Naturgiften’ (Schlangengifte / Pilzgifte / Froschgifte / Fischgifte  …) macht man immer wieder die Entdeckung, dass häufig die Wirkung des Giftes dadurch so fatal ist, dass der Giftstoff dafür sorgt, dass ein eigentlich im Körper vorhandener (und letzten Endes auch lebenswichtiger) Stoff in Unmengen vom Körper produziert wird und er sich dadurch letztlich selbst vergiftet.

Um diesen Prozess umzukehren bzw. den Körper wieder an die normale Stoffkonzentration heranzuführen muss ein ‚Gegengift’ daher versuchen, eigene Körperstoffe kurzfristig stark abzubauen (gegen den ’Willen’ des Körpers) und anschließend den Körper zur Stoffproduktion auf ‚normalem’ Niveau zu bringen.

Zur Darstellung und Berechnung derartiger Ansätze kann man mathematische Funktionsmodelle zu Hilfe nehmen und versuchen, diese Modelluntersuchungen zu übertragen bzw. zu interpretieren.

Die Funktionenschar  `f_a(x) = (a*ln^2(x))/x^2 + a   (a > 0)` stellt ein solches Hilfsmodell der Stoffproduktion in der Zeit dar, wobei eine sinnvolle Interpretation der Funktionswerte wegen des Logarithmus erst ab `x ~~ 1/e`  sinnvoll ist.

  1. Untersuchen Sie diese Funktionenschar mit Hilfe der Standardmittel der Analysis und interpretieren Sie dabei die Ergebnisse für das Modell.
  2. Zeigen Sie mit Hilfe der Integrationsregeln, dass `F_a(x) = (-a*(ln^2x + 2ln x - x^2 + 2))/x` eine Stammfunktionsschar ist und berechnen Sie die Fläche unter `f_a(x)` im Intervall `[1;e]` und geben Sie an, für welches a diese Fläche eine Größe von 1 FE hätte.
  3. Berechnen Sie die gesamte Überproduktion des körpereigenen Stoffes im Modell innerhalb der (unendlichen) Zeit, wenn a die Standardproduktionsmenge angibt.

Quotientenregel in Kurzform:

`(u/v)^' = (u'*v - v'*u)/v^2`

und

Falls `t(x) = (ln^2 x)/x^2`

`rArr T(x) = ( - ln^2 x  - 2ln x - 2)/x`

Kugelfisch / Satansröhrling / Grüne Mamba / Pfeilgiftfrosch

Quelle: https://pixbay.com

 

 

©2024 Net-Schulbuch.de
©2024 NET-SCHULBUCH.DE

10.09  0.1676  8.1.28