Druckversion vom 27.07.2024 04:41 Uhr
Startseite Vorkurs Weitere Gleichungen und Funktionen Funktionsbegriff
Funktionsbegriff - Lehrtext
Eine Zuordnung zwischen den Elementen einer Menge D und den Elementen einer Menge W heißt Funktion, wenn diese Zuordnung eindeutig ist. Eindeutig heißt, dass einem Element der Menge D höchstens ein Element der Menge W zugeordnet wird. Die Art der Zuordnung wird auch Zuordnungsvorschrift genannt.
Beispiel 1:
Betrachtet werden die Wochentage Montag (28.03.2022) bis Freitag (01.04.20022). Diesen Tagen wird der Schlusskurs des DAX (Deutscher Aktienindex) um jeweils 17.00 Uhr zugeordnet. Dies ergibt folgende Tabelle:
| Wochentag | Montag | Dienstag | Mittwoch | Donnerstag | Freitag |
|---|---|---|---|---|---|
| 14417 | 14820 | 14606 | 14414 | 14446 |
Die Menge D besteht also aus den 5 Wochentagen, die Menge W aus Zahlen (welche hier alle verschieden sind).
Die Zuordnung/Zuordnungsvorschrift lautet: Wochentag → Kurs (gelesen: "Wochentag wird zugeordnet Kurs").
Beispiel 2:
Der Seitenlänge eines Quadrats wird der Flächeninhalt des Quadrats zugeordnet. Wird die Seitenlänge mit der Variablen x bezeichnet, so lautet die Zuordnung x → x2. Gibt man der Funktion einen Namen (üblich sind kleine Buchstaben wie f und g), so schreibt man:
f: x → x2 (gelesen: "Funktion f mit x wird zugeordnet x2") oder f(x) = x2 (gelesen: "f von x gleich x2") oder f: y = x2 (gelesen: "Funktion f mit y gleich x2")
f: x → x2 heißt Zuordnung/Zuordnungsvorschrift; f(x) = x2 und y = x2 heißen Funktionsgleichungen; x2 heißt Funktionsterm.
Die Menge D heißt Definitionsmenge und wird auch unter Verwendung des Funktionsnamens mit Df bezeichnet.
Die Menge W heißt Wertemenge und wird auch unter Verwendung des Funktionsnamens mit Wf bezeichnet.
In vorstehender Definiton sind bereits folgende Darstellungsarten genannt worden:
1. Zuordnung/Zuordnungsvorschrift (x → x2)
2. Funktionsgleichung (f(x) = x2 bzw. y = x2)
3. Wertetabelle
| x | 1 | 1,5 | 2 | 2,5 | 3 |
| y | 1 | 2,25 | 4 | 6,25 | 9 |
4. Funktionsgraph
|
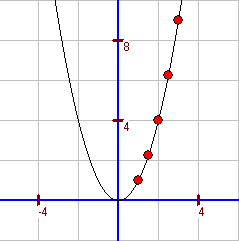
Handelt es sich bei der Definitionsmenge und der Wertemenge um Zahlenmengen (wie im vorliegenden Fall), so lassen sich der x-Wert und der zugehörige y-Wert als Punktkoordinaten interpretieren. Diese Punkte und auch ihre "geschickte" Verbindung miteinander heißt Funktionsgraph. Anmerkung: Im Sachkontext des Flächeninhalts eines Quadrats entfällt natürlich der linke Parabelast. |
 |
Beispiel: f(x) = x2 - x
Setzt man rechts für x eine Zahl ein, z.B. -3, so kann man ausrechnen, welchen Wert der Funktionsterm annimmt (bzw. was sich auf der rechten Seite ergibt). Das Ergebnis nennt man Funktionswert oder auch y-Wert. Die Aufforderung, eine solche Rechnung auszuführen, wird kurz geschrieben als f(-3). Das heißt: Setzen Sie in der Funktion f auf der rechten Seite überall, wo x steht, die Zahl -3 ein. Da mit der -3 noch Rechenoperationen wie "hoch 2" auszuführen sind, setzen Sie vorsichtshalber die einzusetzende Zahl in Klammern.
f(-3) = (-3)2 - (-3) = 9 + 3 = 12
Folgende Aufforderungen bedeuten alle dasselbe (statt x-Wert sagt man auch Stelle):
- "Berechnen Sie den Funktionswert an der Stelle -3."
- "Welchen Wert nimmt der Funktionsterm für x = -3 an?"
- "Welchen y-Wert hat der Punkt auf dem Graphen zu f an der Stelle -3?"
- "Berechnen Sie f(x) für x = -3."
- "Bestimmen Sie f(-3)."
- "Bestimmen Sie zu f die fehlende Punktkoordinaten P(-3; ?)."
Statt konkreter Zahlen kann man auch Variablen, Terme oder Funktionen für x einsetzen:
f(h) = h² - h
f(p + q) = (p + q)² - (p + q) = p² + 2pq + q² - p – q
Im vorhergehenden Abschnitt musste zu einem gegebenen x-Wert der Funktionswert oder y-Wert berechnet werden. Den Auftrag kann man auch umkehren: Berechnen Sie zu einem gegebenen Funktionswert den zugehörigen x-Wert.
In dem Fall ist bekannt, welchen Wert der Funktionsterm auf der rechten Seite der Funktionsgleichung hat. Gesucht ist der passende x-Wert.
Beispiel 1:
Gegeben ist f(x) = x5. Berechnen Sie x für f(x)=1.
x5 = 1; also x = 1.
Antwortmöglichkeiten: f(1) = 1 oder: Der Graph geht durch den Punkt P(1/1).
Beispiel 2:
Gegeben ist f(x) = x4. Berechnen Sie x für f(x)=1.
x4 = 1; hier gibt es zwei Lösungen: x1 = 1 und x2 = -1.
Antwortmöglichkeiten: f(1) = 1 und f(-1) = 1 oder: Der Graph geht durch P(1/1) und Q(-1/1).
Achtung:
- Zu einem y-Wert kann es mehrere x-Werte geben. Bei Potenzfunktionen mit geradem Exponenten kann es einen, zwei oder auch keinen x-Wert geben; bei ungeradem Exponenten gibt es immer genau einen x-Wert als Lösung. Zur Erinnerung: Zu einem x-Wert gibt es nie mehrere y-Werte.
- Das Berechnen von x-Werten zu einem gegebenen y-Wert bedeutet immer: Sie müssen folgende Gleichung lösen: Funktionsterm = y-Wert.
|
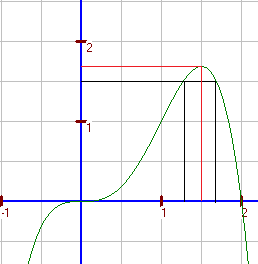
Beispiel 1: a) Welches ist der Funktionswert an der Stelle 1,5? b) Welcher x- Wert gehört zu y = 1,5? Ergänzung: zu a): Die Funktionsgleichung ist f(x) = -x4 + 2x3. f(1,5) ≈ 1,69 Zu b): -x4 + 2x3 = 1,5. Die Gleichung ist mit normalen Mitteln nicht zu lösen. |
 |
|
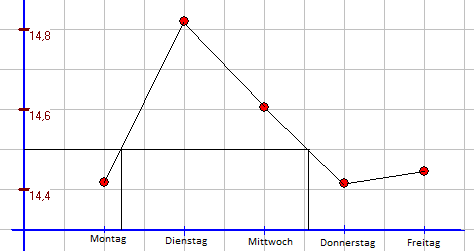
Beispiel 2: Betrachtet wird obiges Beispiel des DAX-Kurses. a) Wie hoch war der Kurs am Dienstag um 15.00 Uhr? Diese Frage lässt sich nicht bantworten, da der Graph nur angenähert die Kursentwicklung widergibt. In Wirklichkeit ist die Kursentwicklung nicht linear. Auch hat z.B. der Zeitpunkt "Montag 17.00 Uhr" gleichzeitig die Bedeutung "Dienstag 9.00 Uhr", da in der Zwischenzeit kein Aktienkurs notiert wird. b) Wann erreichte der Kurs 14500 Punkte? Man kann lediglich sagen: irgendwann am Dienstag und irgenwann am Donnerstag jeweils zwischen 9.00 Uhr und 17.00 Uhr. |
 |
|
Welche der folgenden 6 Funktionen `f_1` bis `f_6` gehören zu den Graphen im rechten Bild? a) `f_1(x)=1/2*x^2+2` b) `f_2(x)=-x^4+2x^3` c) `f_3(x)=x^3-x` d) `f_4(x)=x^3-2x^2+x` e) `f_5(x)=x^2+3` f) `f_6(x)=-2x+3` Lösung: Es gibt nur einen linearen Funktionsgraphen und eine lineare Funktion, nämlich Graph a und `f_6(x)` . Da Achsenabschnitt und Steigung passen, ist Graph a der zu `f_6(x)` zugehörige Graph. Der Scheitelpunkt der Parabel d ist (0; 3). Hierzu passt nur `f_5(x)`. Da `f_5(1)=4`, ist Graph d der zu `f_5(x)` gehörige Graph. Wertetabelle für Graph c:
Hierzu passt nur `f_2(x)`. Dass dies tatsächlich die Lösung ist, wird später im Rahmen der Analysis behandelt. Wertetabelle für Graph b:
Hierzu passt nur `f_3(x)`. Dass dies tatsächlich die Lösung ist, wird später im Rahmen der Analysis behandelt. |
 |
Verfahren zur Identifizierung von Graphen und zugehörigen Funktionsgleichungen:
- Vergleich von charakteristischen Punkten mit einer Wertetabelle.
- Vergleich von charakteristischen Eigenschaften Ihnen bekannter Funktionsklassen mit den vorliegenden Graphen (Linearität, Scheitelpunkt, Symmetrie).
|
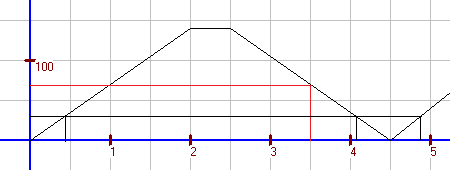
Ein Schüler gelangt von seiner Wohnung über eine geradlinige Straße zu seiner Schule. Betrachtet wird die Funktion "Dauer des Weges → Entfernung von der Wohnung". In nebenstehender Zeichnung sind auf der x-Achse die Minuten seit dem Verlassen der Wohnung und auf der y-Achse die Entfernung von der Wohnung in Metern abgetragen. Beschreibung des Schulweges: a) Wie weit ist der Schüler nach 3,5 Minuten von der Wohnung entfernt? b) Zu welchen Zeitpunkten ist er 25 m von der Wohnung entfernt? (Eine exakte Berechnung wird als Aufgabe im Augabenteil gestellt.) Hinweis: In einer solchen Realsituation verwendet man oft statt der Variablen x andere Variablen, z. B. t für die Zeit in Minuten (t als Abkürzung für time). Dann schreibt man: f: t → f(t), wobei t die Zeit in Minuten seit Verlasssen der Wohnung und f(t) die Entfernung von der Wohnung in Metern ist. Ein Funktionterm für f(t) kann in diesem Fall nicht als geschlossener Term, sondern muss für die 4 Geradenstücke getrennt angegeben werden. |
 |

