Druckversion vom 27.07.2024 09:06 Uhr
Startseite Vorkurs Weitere Gleichungen und Funktionen Quadratische Funktionen (Parabeln)
Quadratische Funktionen - Lösungen
 Aufgabe 1 Aufgabe 1 |
||||
|
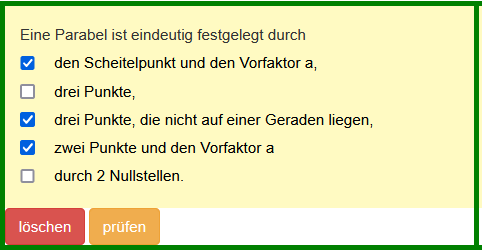
Klicken Sie die richtigen Aussagen an:
|
 Aufgabe 2 Aufgabe 2 |
||||||||
|
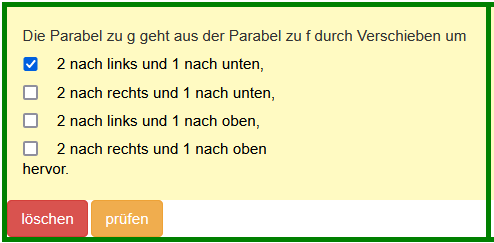
Klicken Sie die richtigen Aussagen an:
|
 Aufgabe 3 Aufgabe 3 |
|
Geben Sie die charakteristischen Eigenschaften (siehe Lehrtext) der Parabeln an und skizzieren Sie die Parabeln.
|
Lösungen
|
a. `f(x)=(x-4)^2+2` Da `a=1`, handelt es sich um eine nach oben geöffnete Normalparabel. Scheitelpunkt: S(4; 2) Nullstellen existieren nicht, da der Scheitelpunkt oberhalb der x-Achse liegt und die Parabel nach oben geöffnet ist. Alle Funktionswerte sind größer als 2. |
 |
|
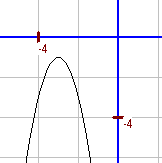
b. `f(x)=-2(x+3)^2-1` Da `a=-2`, handelt es sich um eine nach unten geöffnete und gegenüber einer Normalparabel gestreckte Parabel (schmalere Öffnung als eine Normalparabel). Scheitelpunkt: S(-3; -1) Nullstellen existieren nicht, da der Scheitelpunkt unterhalb der x-Achse liegt und die Parabel nach unten geöffnet ist. Alle Funktionswerte sind kleiner als -1. |
 |
|
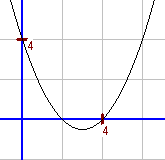
c. `f(x)=0,5*(x-2)*(x-4)` Da `a=0","5`, handelt es sich um eine nach oben geöffnete und gegenüber einer Normalparabel gestauchte Parabel (breitere Öffnung als eine Normalparabel). Die Nullstellen sind `x_1=2` und `x_2=4`. Also ist der x-Wert des Scheitelpunktes `(2+4)/2=3`. Wegen `f(3)=-0","5` folgt S(3; -0,5). Für `x < 2` oder `x > 4` sind alle Funktionswerte positiv. Für `2 < x < 4` sind alle Funktionswerte negativ. |
 |
|
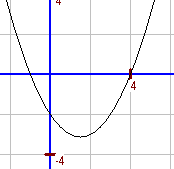
d. `f(x)=-(x-1)^2+9` Da `a=-1`, handelt es sich um eine nach unten geöffnete Normalparabel. Scheitelpunkt S(1; 9) Nullstellen: `-(x-1)^2+9=0 hArr (x-1)^2=9` `hArr x-1=3 vv x-1=-3` `x_1=4` und `x_2=-2` Für `x < -2` oder `x > 4` sind alle Funktionswerte negativ. Für `-2 < x < 4` sind alle Funktionswerte positiv. |
 |
|
e. `f(x)=0","5*x^2-1","5x-2` Da `a=0","5`, handelt es sich um eine nach oben geöffnete und gegenüber einer Normalparabel gestauchte Parabel (breitere Öffnung als eine Normalparabel). Nullstellen: `0","5*x^2-1","5x-2=0 hArr x^2-3x-4=0` `x_(1",")=3/2+-sqrt(9/4+4)=3/2+-5/2` `x_1=4` und `x_2=-1` Also ist der x-Wert des Scheitelpunktes `(4+(-1))/2=1","5`. Wegen `f(1","5)=-3","125` folgt S(1,5; -3,125). Für `x < -1` oder `x > 4` sind alle Funktionswerte positiv. Für `-1 < x < 4` sind alle Funktionswerte negativ.
|
 |
 Aufgabe 4 Aufgabe 4 |
|
|
Ermitteln Sie die Funktionsvorschrift in Normal- und in Scheitelpunktform. |
 |
Lösung
Schwarze Parabel:
Scheitelpunkt S(-2; 4), also: `f(x)=a*(x+2)^2+4`
`a=-1` (Geht man vom Scheitelpunkt 1 nach links oder rechts und 1 nach unten, so trifft man auf einen Punkt der Parabel.)
Scheitelpunktform: `f(x)=-(x+2)^2+4`
`-(x+2)^2+4=-(x^2+4x+4)+4=-x^2-4x`
Normalform: `f(x)=-x^2-4x`
Rote Parabel:
Scheitelpunkt S(2; 3), also `f(x)=a*(x-2)^2+3`
`a= 1/2` (Geht man vom Scheitelpunkt 1 nach links oder rechts und `1/2` nach oben, so trifft man auf eine Punkt der Parabel.)
Alternativ: (0; 5) ist ein Punkt der Parabel, d.h. `a*(0-2)^2+3=5 hArr 4a=2 hArr a=1/2`
Scheitelpunktform: `f(x)=1/2*(x-2)^2+3`
`1/2*(x-2)^2+3=1/2*(x^2-4x+4)+3=1/2x^2-2x+5`
Normalform: `f(x)=1/2x^2-2x+5`
 Aufgabe 5 Aufgabe 5 |
|
Bestimmen Sie Scheitelpunkt- und Normalform. Skizzieren Sie die Graphen.
|
Lösungen
|
a. S(-2; 3), also `f(x)=a*(x+2)^2+3` Aus `f(1)=21` folgt `a*(1+2)^2+3=21 hArr 9a=18 hArr a=2` Scheitelpunktform: `f(x)=2*(x+2)^2+3` `2*(x+2)^2+3=2*(x^2+4x+4)+3=2x^2+8x+11` Normalform: `f(x)=2x^2+8x+11` |
 |
|
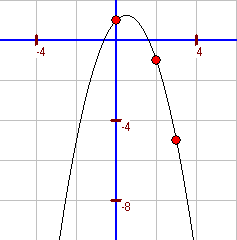
b. In die allgemeine Normalform `f(x)=ax^2+bx+c` werden die Koordinaten der gegebenen Punkte eingesetzt. A: `a*2^2+b*2+c=-1` B: `a*0^2+b*0+c=1` C: `a*3^2+b*3+c=-5` Aus der 2. Gleichung folgt `c=1`. Somit ergibt sich mit der 1. und 3. Gleichung I: `4a+2b+1=-1 hArr 4a+2b=-2` II: `9a+3b+1=-5 hArr 9a+3b=-6` III: `-6a=6` (3·I - 2·II) `a=-1` Einsetzen von `a=-1` in I ergibt `-4+2b=-2 hArr b=1` Somit lautet die Normalform: `f(x)=-x^2+x+1` Bestimmung der Scheitelpunktform: `-x^2+x+1=0 hArr x^2-x-1=0; (p=-1, q= -1)` Die x-Koordinate des Scheitelpunktes hat den Wert `-p/2=1/2` `f(1/2)=-1/4+1/2+1=5/4` Scheitelpunktform: `f(x)=-(x-1/2)^2+5/4` |
 |
|
c. Mit A und B sind zwei Punkte auf der x-Achse gegeben. Die x-Koordinaten dieser Punkte sind folglich Nullstellen. Somit folgt `f(x)=a*(x-2)*(x-6)` Setzt man die Koordinaten von C ein, so erhält man: `a*(8-2)*(8-6)=2 hArr a=1/6` Normalenform: `f(x)=1/6*(x-2)*(x-6)=1/6*(x^2-8x+12)=1/6x^2-4/3x+2` Die x-Koordinate des Scheitelpunkts ist `(2+6)/2 = 4` Da `f(4)=8/3-16/3+2=-2/3` ergibt sich als Scheitelpunktform: `f(x)=1/6*(x-4)^2-2/3` |
 |
|
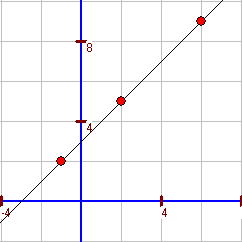
d. In die allgemeine Normalform `f(x)=ax^2+bx+c` werden die Koordinaten der gegebenen Punkte eingesetzt. A: `a*(-1)^2+b*(-1)+c=2 hArr a-b+c=2` (I) B: `a*2^2+b*2+c=5 hArr 4a+2b+c=5` (II) C: `a*6^2+b*6+c=9 hArr 36a+6b+c=9` (III) IV: `3a+3b=3 hArr a+b=1` (II - I) V: `35a+7b=7 hArr 5a+b=1` (III- I) VI: `4a=0` (V-IV) `a=0` Es gibt also keine Parabel, auf der die drei Punkte liegen. Eine weitere Rechnung ergibt `b=1` und `c=3`. Somit folgt als Funktionsgleichung `f(x)=x+3` (Die drei Punkte liegen auf einer Geraden.) |
 |
 Aufgabe 6 Aufgabe 6 |
|
Bestimmen Sie die Schnittpunkte der folgenden Parabeln:
|
Lösungen
|
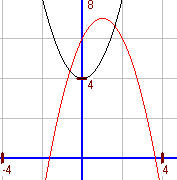
a. `x^2+4=-x^2+2x+6 hArr 2x^2-2x-2=0 hArr x^2-x-1=0` `x_(1","2)=1/2+-sqrt(1/4+1)~~1/2+-1","12` `x_1~~1","62` und `x_2~~-0","62` `f(1","62)~~6","62` und `f(-0","62)~~4","38` Die Parabeln schneiden sich in den Punkten (1,62; 6,62) und (-0,62; 4,38). |
 |
|
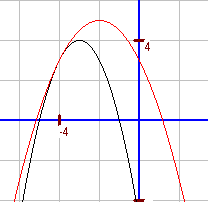
b. `-(x+3)^2+4=-0","5(x+2)^2+5` `hArr -(x^2+6x+9)+4=-0","5(x^2+4x+4)+5` `hArr -x^2-6x-5=-0","5x^2-2x+3` `hArr -0","5x^2-4x-8=0` `hArr x^2+8x+16=0` `hArr (x+4)^2=0 hArr x=-4` Einziger Schnittpunkt ist (-4; 3). |
 |
|
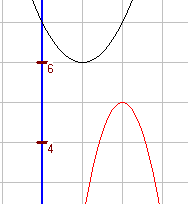
c. `f(x)=(x-1)^2+6` und `g(x)=-3(x-2)^2+5` Der Scheitelpunkt der Parabel zu f liegt höher als der Scheitelpunkt der Parabel zu g. Da die Parabel zu f nach oben und die andere Parabel nach unten geöffnet ist, schneiden sich die beiden Parabeln nicht. |
 |
 Aufgabe 7 Aufgabe 7 |
|
Gegeben ist die Parabel zu `f(x)=x^2`. Berechnen Sie die Schnittpunkte der Parabel mit den folgenden Geraden:
|
Lösungen
|
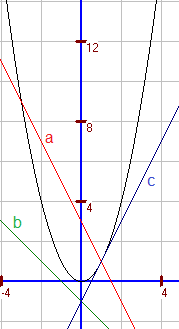
a. `x^2=-2x+3 hArr x^2+2x-3=0` `x_(1","2)=-1+-sqrt(1+3)` `x_1=1` und `x_2=-3`. Die Schnittpunkte sind (1; 1) und (-3; 9). b. `x^2=-x-1 hArr x^2+x+1=0` `x_(1","2)=-0","5+-sqrt(0","25-1)` Gerade und Parabel schneiden sich nicht. c. `x^2=2x-1 hArr x^2-2x+1=0` `hArr (x-1)^2=0 hArr x=1` Gerade und Parabel schneiden sich im Punkt (1; 1). Hinweis für später: Gerade und Parabel berühren sich in diesem Punkt. Die Gerade ist Tangente an die Parabel. |
 |
 Aufgabe 8 Aufgabe 8 |
|
|
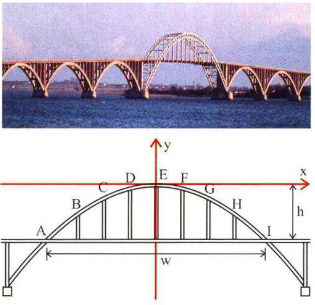
Bestimmen Sie die Gleichung der Funktion, deren Gaph den Brückenbogen darstellt (w = 80 m, h= 20 m).
|
 |
Lösung
Der Skizze entnimmt man, dass der Scheitelpunkt bei (0; 0) liegt. Also gilt `f(x)=a*(x-0)^2+0=a*x^2`.
Ein weiterer Punkt ist (40; -20), d. h. `f(40)=-20 hArr a*1600=-20 hArr a=-1/80`
Der Brückenbogen kann durch `f(x)=-1/80*x^2` beschrieben werden.
 Aufgabe 9 Aufgabe 9 |
|
|
Ein Fußballspielr schießt eine Flanke. Die Flugbahn des Balles kann durch folgende Parabel beschrieben werden ; `f(x)=-0,00625x^2+0,25x` beschrieben werden. Dabei ist x die horizontale Entfernung und f(x) die Höhe des Balles über dem Rasen.
|
 |
Lösungen
a.
`f(5)=-0,00625*25+0,25*5~~1,1 m`
Bei einer horizontalen Entfernung von 5 m beträgt die Höhe des Balles über dem Rasen ca. 1,1 m.
b.
Zu bestimmen ist der Scheitelpunkt. Die x-Koordinate des Scheitelpunktes ist identisch mit dem Wert `-p/2` der p-q-Formel. `p=-(0","25)/(0","00625)=-40` (Beachten Sie, dass vor Anwendung der p-q-Formel durch den Vorfaktor von `x^2` dividiert werden muss).
Die größte Höhe des Balles beträgt folglich `-p/2=20` m.
c.
`f(20)=2,5`.
Der Spieler erreicht den Ball zum Köpfen nicht.
 Aufgabe 10 Aufgabe 10 |
|
|
Um Hühnern freien Auslauf zu bieten, werden oft transportable Käfige (im Bild rot) auf einer Wiese abgestellt und eine rechteckige Futterfläche (im Bild schwarz) eingezäunt. Zur Einzäunung stehen 120 m Zaunmaterial zur Verfügung.
|
Quelle: pixabay.com |
Lösung
a.
Für eine Längs- und eine Querseite steht zusammen die Hälfte des Zaunmaterials, also 60 m zur Verfügung. Da die Länge der Querseite x beträgt, bleibt für die Längsseite 60-x übrig. Somit hat die eingezäunte Flächen den Inhalt `(60-x)*x=60x-x^2`.
b.
Für die x-Koordinate `x_s` des Scheitelpunktes gilt `x_s=-p/2`. Da `p=-60` (beachten Sie, dass vor Anwendung der p-q-Formel durch den Vorfaktor von `x^2` dividiert werden muss), folgt: `x_s=30`.
Alternativ: `-x^2+60x=0 hArr -x(x-60)=0 hArr x=0 vv x=60`
Da die x-Koordinate des Scheitelpunktes in der Mitte der beiden Nullstellen liegt, folgt `x_s=30`.
Da es sich um eine nach unten geöffnete Parabel handelt, ist der y-Wert des Scheitelpunktes der größte Funktionswert.
`f(30)=-30^2+60*30=900`.
Der größte Flächeninhalt, der durch die Einzäunung erreicht werden kann, beträgt 900 m2. Er wird erreicht, wenn ein Quadrat der Seitenlänge 30 m eingezäunt wird.
|
Gegeben ist `f(x)=(x+1)^2+1` und `g(x)=m*x+1`. Für welche Steigungen m haben Parabel und Gerade 0, 1, 2 Schnittpunkte? Skizzieren Sie den Sachverhalt. |
Lösung
|
`(x+1)^2+1=m*x+1 hArr x^2+2x+1=m*x hArr x^2+(2-m)*x+1=0` `x_(1","2)=-(2-m)/2+-sqrt((2-m)^2/4-1)` `=-(2-m)/2+-sqrt((4-4m+m^2)/4-1)` `=-(2-m)/2+-sqrt((m^2-4m)/4)` Ein Schnittpunkt ergibt sich, wenn `m^2-4m=0 hArr m^2=4m hArr m=4 vv m=0` Für `m=0` (rote Gerade) ergibt sich der Schnittpunkt (-1; 1), also der Scheitelpunkt der Parabel. Für `m=4` (grüne Gerade) ergibt sich der Schnittpunkt (1; 5). Hinweis für später: Beide Schnittpunkte werden auch Berührpunkte genannt und die beiden Geraden heißen auch Tangenten an die Parabel. Um zu untersuchen, für welche m der Ausdruck unter der Wurzel positiv/negativ ist, wird folgende Funktion betrachtet: `h(m)=m^2-4m`. Hierbei handelt es sich um die Gleichung einer nach oben geöffneten Parabel mit den Nullstellen 0 und 4 (wie soeben berechnet). Daraus folgt, dass alle Funktionswerte von h für `0 < m < 4` negativ sind. Für `m < 0` und `m > 4` sind die Funktionswerte positiv. Die Funktionswerte von h sind aber gerade die Werte unter der obigen Wurzel und entscheiden folglich darüber, wie viel Schnittpunkte es gibt. Alle Geraden, die im blauen Bereich verlaufen `(0 < m < 4)`, haben keinen Schnittpunkt mit der Parabel. Alle Geraden, die im rosa Bereich `(m < 0)` oder im gelben Bereich `(m > 4)` verlaufen, schneiden die Parabel zweimal. |
 |