Druckversion vom 27.07.2024 08:51 Uhr
Startseite Vorkurs Weitere Gleichungen und Funktionen Quadratische Funktionen (Parabeln)
Quadratische Funktionen - Aufgaben
Weitere Aufgaben finden Sie hier und hier
 Aufgabe 1 Aufgabe 1 |
||||
|
Klicken Sie die richtigen Aussagen an:
|
 Aufgabe 2 Aufgabe 2 |
||||||||
|
Klicken Sie die richtigen Aussagen an:
|
 Aufgabe 3 Aufgabe 3 |
|
Geben Sie die charakteristischen Eigenschaften (siehe Lehrtext) der Parabeln an und skizzieren Sie die Parabeln.
|
 Aufgabe 4 Aufgabe 4 |
|
|
Ermitteln Sie die Funktionsvorschrift in Normal- und in Scheitelpunktform. |
 |
 Aufgabe 5 Aufgabe 5 |
|
Bestimmen Sie Scheitelpunkt- und Normalform. Skizzieren Sie die Graphen.
|
 Aufgabe 6 Aufgabe 6 |
|
Bestimmen Sie die Schnittpunkte der folgenden Parabeln:
|
 Aufgabe 7 Aufgabe 7 |
|
Gegeben ist die Parabel zu `f(x)=x^2`. Berechnen Sie die Schnittpunkte der Parabel mit den folgenden Geraden:
|
 Aufgabe 8 Aufgabe 8 |
|
|
Bestimmen Sie die Gleichung der Funktion, deren Gaph den Brückenbogen darstellt (w = 80 m, h= 20 m). |
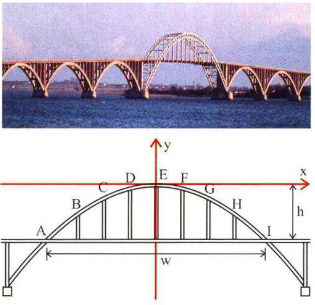 |
 Aufgabe 9 Aufgabe 9 |
|
|
Ein Fußballspieler schießt eine Flanke. Die Flugbahn des Balles kann durch folgende Parabel beschrieben werden ; `f(x)=-0,00625x^2+0,25x` beschrieben werden. Dabei ist x die horizontale Entfernung und f(x) die Höhe des Balles über dem Rasen.
|
 |
 Aufgabe 10 Aufgabe 10 |
|
|
Um Hühnern freien Auslauf zu bieten, werden oft transportable Käfige (im Bild rot) auf einer Wiese abgestellt und eine rechteckige Futterfläche (im Bild schwarz) eingezäunt. Zur Einzäunung stehen 120 m Zaunmaterial zur Verfügung.
|
Quelle: pixabay.com |
|
Gegeben ist `f(x)=(x+1)^2+1` und `g(x)=m*x+1`. Für welche Steigungen m haben Parabel und Gerade 0, 1, 2 Schnittpunkte? Skizzieren Sie den Sachverhalt. |


