
Quelle: https://nwm2.net-schulbuch.de/index.php
Druckversion vom 27.07.2024 09:54 Uhr
Startseite
Aktuelles Thema
Aktuelle Themen und Neues im digitalen Mathebuch
 Aufgabe (Voraussetzung: Exponentialfunktionen) Aufgabe (Voraussetzung: Exponentialfunktionen) |
|
Die Ausbreitung der Wölfe in Deutschland wird heftig diskutiert. Hier zwei Beispiele dazu:
Wölfe breiten sich in Deutschland aus: Kritik am Schutzstatus
"Aktuell ist der Wolf in Deutschland streng geschützt und darf nur unter ganz bestimmten Voraussetzungen gejagt werden. Doch die Zahl der Wölfe in Deutschland steigt." meldet dpa am 5.2. 2023 (siehe dazu Bericht in der Berliner Zeitung)
Nach DNA-Test: Minister bezeichnet Gerüchte über angeblichen Wolfsangriff auf Menschen als "Fake News"
In Mecklenburg-Vorpommern gab es Gerüchte über einen Wolfsangriff auf einen Menschen. Eine DNA-Untersuchung entlastet die Tiere. Der Landwirtschaftsminister wehrt sich zudem gegen Verleumdungen. (28.4.2023 STERN)
|
Das Wolfsrudel ist eine Kleinfamilie. Es besteht aus dem Elternpaar, welches meist auf Lebenszeit verbunden bleibt, den Welpen und den Jungtieren aus dem Vorjahr (Jährlinge). Die Größe des Rudels schwankt im Jahresverlauf meist zwischen 5 und 10 Wölfen. Die Schwankung der Rudelstärke wird durch die Geburt der Welpen, das Abwandern der Jährlinge und durch Todesfälle beeinflusst. Unter bestimmten Bedingungen können auch fremde Wölfe in das Rudel integriert werden.
Ein Wolfsterritorium muss so groß sein, dass die Elterntiere jedes Jahr genug Beute machen können, um ihren Nachwuchs großzuziehen. Je weniger Beutetiere in einer Region leben, desto größer muss das Gebiet sein, in dem das Wolfsrudel zu Hause ist. In Deutschland liegen die Reviergrößen bei rund 200 km².
Die Jungwölfe aus dem elterlichen Territorium ziehen auf der Suche nach einem Partner in der Regel mit Erreichen der Geschlechtsreife in Ihrem zweiten Lebensjahr davon. Da andererseits jedes Jahr neue Welpen geboren werden, bleibt die Anzahl der Wölfe in einem Territorium relativ konstant.
Quelle: http://www.wolf-sachsen.de/de/leben-im-rudel
Quelle für die Zahlen:
Dokumentations- und Beratungsstelle des Bundes zum Thema Wolf (DBBW)
https://www.dbb-wolf.de/Wolfsvorkommen/territorien/entwicklung-diagramm
|
|
Jahr
|
|
Rudel
|
|
Paare
|
|
Einzeltiere
|
|
|
|
2022/23
|
|
47
|
+
|
5
|
+
|
8
|
=
|
60
|
|
2021/22
|
|
161
|
+
|
44
|
+
|
21
|
=
|
226
|
|
2020/21
|
|
158
|
+
|
35
|
+
|
22
|
=
|
215
|
|
2019/20
|
|
131
|
+
|
47
|
+
|
10
|
=
|
188
|
|
2018/19
|
|
105
|
+
|
42
|
+
|
12
|
=
|
159
|
|
2017/18
|
|
77
|
+
|
41
|
+
|
4
|
=
|
122
|
|
2016/17
|
|
60
|
+
|
24
|
+
|
3
|
=
|
87
|
|
2015/16
|
|
47
|
+
|
21
|
+
|
4
|
=
|
72
|
|
2014/15
|
|
32
|
+
|
19
|
+
|
6
|
=
|
57
|
|
2013/14
|
|
25
|
+
|
12
|
+
|
4
|
=
|
41
|
|
2012/13
|
|
17
|
+
|
12
|
+
|
3
|
=
|
32
|
|
2011/12
|
|
14
|
+
|
5
|
+
|
4
|
=
|
23
|
|
2010/11
|
|
7
|
+
|
7
|
+
|
6
|
=
|
20
|
|
2009/10
|
|
7
|
+
|
2
|
+
|
4
|
=
|
13
|
|
2008/09
|
|
5
|
+
|
3
|
+
|
4
|
=
|
12
|
|
2007/08
|
|
3
|
+
|
3
|
+
|
2
|
=
|
8
|
|
2006/07
|
|
3
|
+
|
0
|
+
|
1
|
=
|
4
|
|
2005/06
|
|
2
|
+
|
1
|
+
|
0
|
=
|
3
|
|
2004/05
|
|
1
|
+
|
2
|
+
|
0
|
=
|
3
|
|
2003/04
|
|
1
|
+
|
0
|
+
|
1
|
=
|
2
|
|
2002/03
|
|
1
|
+
|
0
|
+
|
1
|
=
|
2
|
|
2001/02
|
|
1
|
+
|
0
|
+
|
0
|
=
|
1
|
|
2000/01
|
|
1
|
+
|
0
|
+
|
0
|
=
|
1
|
|
Aufgaben
- Lesen Sie die Informationen im obigen Drop-Down-Panel "Zahlen und Informationen ..." sorgfältig durch.
- Berechnen Sie eine obere Grenze für die Zahl der Wolfrudel in Deutschland. Gehen Sie dabei davon aus, dass alle Flächen – bis auf die für Siedlung und Verkehr – für Wolfsrudel geeignet sind.
- Begründen Sie, warum die jährliche Summe der drei Zahlen in der Tabelle Wolfsvorkommen keine geeignete Information bietet.
- Der Text oben spricht von einer „dynamischen Entwicklung“.
- Untersuchen Sie anhand der Rudelanzahlen, ob man von 2005/06 bis 2020/21 auch von einem exponentiellen Wachstum sprechen kann. Hinweis: Hier können Sie die Zahlen als Excel- oder GeoGebra-Datei herunterladen.
- Berechnen Sie die durchschnittliche Wachstumsrate für diesen Zeitraum.
- Bestimmen Sie das Jahr, in dem die obere Grenze erreicht würde, wenn sich die Wohlsrudel exponentiell vermehren würden.
- Begründen Sie, warum es dazu nicht kommen wird.
- Leiten Sie aus der obigen Tabelle eine Abschätzung für die Zahl der Wölfe in Deutschland ab und untersuchen Sie auch deren Wachstumsdynamik.
- Verfahren Sie alternativ mit der Anzahl der erwachsenen Tiere (älter als 2 Jahre).
|

Bild von steve fehlberg auf Pixabay
|
- Fläche Deutschlands rund `357.581 km^2`, abzüglich 14,5% für Siedlungs- und Verkehrsflächen => `305.731 km^2`. Teilt man die Fläche durch `200 km^2`, so erhält man eine obere Grenze von 1528 Wolfsrudeln.
- Spalte 1 enthält die Zahl der Wolfrudel (5 – 10 Tier), Spalte 2 die Wolfspaare (ohne Nachwuchs) und Spalte 3 die Einzeltiere. Man addiert also „Äpfel mit Birnen“
-
- Die jährliche Wachstumsrate ist nicht überall gleich, liegt aber meistens zwischen 1,25 und 1,5. Die exp. Trendlinie zeigt eine ganz gute Anpassung, wobei das letzte Jahr im untersuchten Zeitraum schon abweicht.
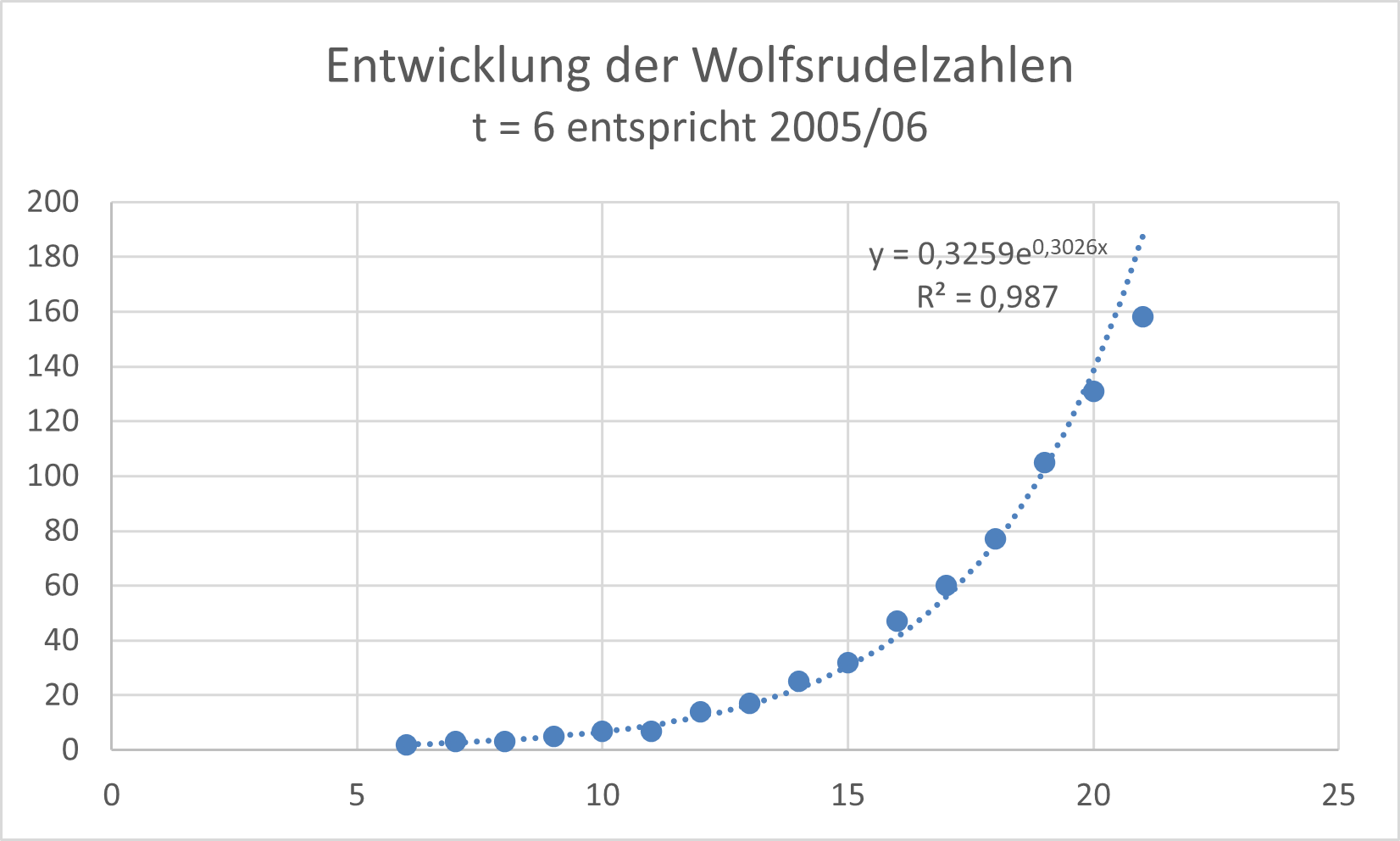
- Die durchschnittliche Wachstumsrate beträgt `root 15 (158/2) ~~ 1,338`.
- Die Wachstumsfunktion wäre dann `f(x) = 2*(1,338)^x`. Die Gleichung `1528 = 2 * (1,338)^x` ergibt nach Logarithmierung: `(ln(764))/(ln(1,338)) = x => x ≈ 22,8`. Die obere Grenze wäre danach im Jahr 2027/28 erreicht.
- Die zur verfügung stehende Nahrung ist nicht überall gleich, evtl. wird dann die Bejagung wieder frei gegeben...
- Für die Zahl der Wölfe wäre eine untere, eine mittlere und eine obere Abschätzung möglich. Dazu nimmt man die Mitgliederzahl der Rudel mit 5 (untere), 7.5 (mittlere) und 10 (obere) Tiere an. Bei den Paaren sind es jeweils 2 und bei den Einzeltieren 1. Daraus ergeben sich die drei Zeitreihen:
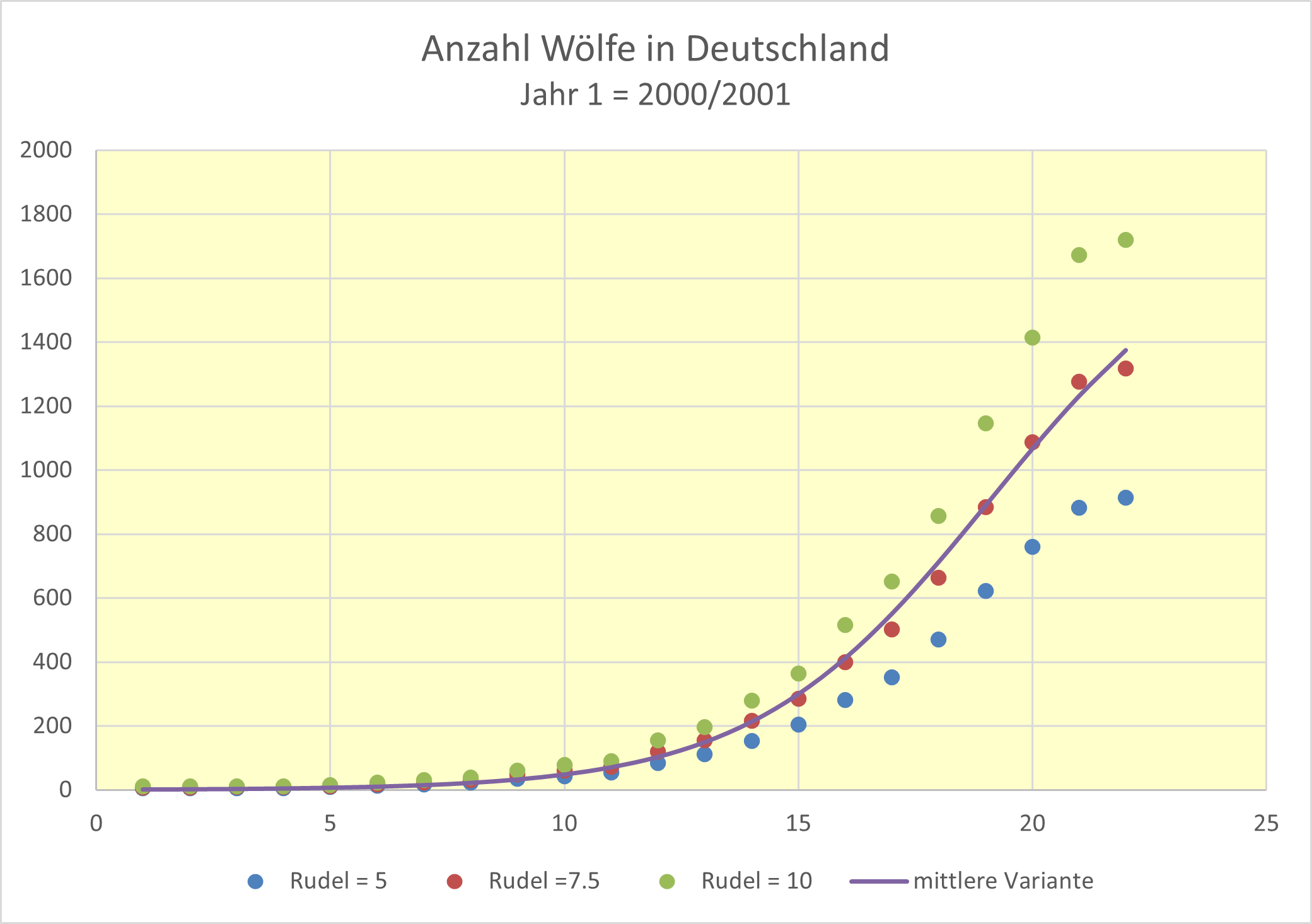
Man sieht, dass ein möglicher exponentieller Trend schon seit einigen Jahren „gekippt“ ist. Für die mittlere Variante ist eine logistische Trendlinie eingezeichnet. Diese hat in etwa einen S-förmigen Verlauf, weil die Zuwachsrate vom Bestand und vom Abstand zur Grenze abhängig ist. Mehr dazu finden Sie unter
Wachstumsprozesse.
- Entsprechendes erhält man auch, wenn man die Zahl der Altwölfe modelliert.
©2024 NET-SCHULBUCH.DE




