Druckversion vom 20.05.2024 01:11 Uhr
Startseite Interaktive Knobeleien
Schiebepuzzle

Jedes Zahlenfeld, das das freie Feld als Nachbarn hat, kann durch einen Mausklick seinen Platz mit dem leeren Feld tauschen.
 bewirkt eine völlig neue Verteilung der Zahlen.
bewirkt eine völlig neue Verteilung der Zahlen.
Nur sichtbar bei der Startliste oder einer unlösbaren Verteilung.
 führt immer zur geordneten Startliste zurück.
führt immer zur geordneten Startliste zurück.
 und
und  zeigen an, ob eine Lösung möglich ist oder nicht.
zeigen an, ob eine Lösung möglich ist oder nicht.
(Näheres im unteren Panel!)
Ein paar Gedanken zur Lösbarkeit des Schiebepuzzles!
(Eine sehr anschauliche Lösung finden Sie z.B. unter https://www.mathe-online.at/galerie/spiel/14-15/14-15.html.)
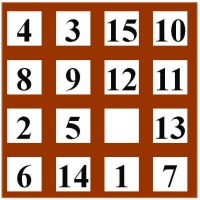
Nach dem Mischen der Felder soll das entstandene Ausgangspuzzle durch Verschieben der einzelnen Zahlen in die "richtige" Reihenfoge gebracht werden.
 `rarr`
`rarr` 
Das Ausgangspuzzle ist nicht korrekt, weil es Zahlen gibt, die nicht in der natürlichen Reihenfolge stehen.
In der ersten Zeile z.B. steht die `4` vor der `3` und die `10` steht hinter der `15`.
Jedes dieser nicht korrekten Puzzle hat also fehlerhafte Reihenfolgen von Zahlen.
Die Anzahl dieser Fehler eines solchen Puzzle könnte man `f` nennen und wie folgt berechnen:
Alle Puzzlezahlen hintereinander geschrieben sind: `4|3|15|10|8|9|12|11|2|5|square|13|6|14|1|7`
Für jede der Zahlen kann man nun angeben, mit welcher anderen Zahl sie eine falsche Reihenfolge bildet.
z.B. für die `\color{blue}12`:
Alle Zahlen, die hinter der `\color{blue}12` stehen und kleiner sind als `\color{blue}12`, bilden mit ihr ein "falsches" Paar:
`4|3|15|10|8|9|\color{blue}12|\color{red}11|\color{red}2|\color{red}5|square|13|\color{red}6|14|\color{red}1|\color{red}7`
Das sind sechs solcher Paare.
Wenn man nun diese falschen Paare für alle `15` Werte nacheinander auf die gleiche Art bildet, ergibt sich die Gesamtzahl der Fehler `f`.
(Alle Werte vor einer Zahl, die größer als die Zahl sind werden somit auch als Paar erfasst!)
Beginnend mit der `\color{blue}4`, die `3` solcher Paare bildet - mit `\color{red}3 |color{red} 2 |color{red}1` - bis zu den Werten der unteren Reihe
`\color{blue}6` mit `1` falschen Paar, `\color{blue}14` mit `2` solchen Paaren und `\color{blue}1` und `\color{blue}7`, die keine solchen Paare bilden - ergibt sich als Gesamtzahl dieser Falschpaare für diese Mischung ein Wert von `f = 53`.
Zum Nachrechnen!
Nun kann man untersuchen, wie sich die Fehlerzahl `f` durch eine Verschiebung ändert.
Sehr einfach ist es mit einer Verschiebung in der Waagerechten.
Da die Reihenfolge der Werte nicht geändert wird, sondern nur die Lage des Leerfeldes, z.B. auf `4|3|15|10|8|9|12|11|2|\color{red}square|\color{red}5|13|6|14|1|7`, bleibt die Fehlerzahl `f` jeweils gleich.
Bei einer Verschiebung in der Senkrechten gibt es zwei Möglichkeiten:
Die zu verschiebende Zahl wird nach oben
 `rarr`
`rarr` 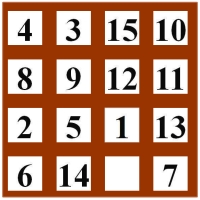
oder nach unten
 `rarr`
`rarr` 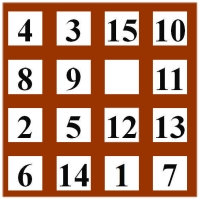
geschoben.
Damit wechselt sie ihren Platz in der Reihenfolge jeweils um genau vier Plätze.
Beim Verschieben nach oben rückt sie vier Plätze in der Liste nach vorne:
`4|3|15|10|8|9|12|11|2|5|\color{red}1|\color{blue}13|\color{blue}6|\color{blue}14|\color{red}square|7`.
Beim Verschieben nach unten um vier Plätze nach hinten:
`4|3|15|10|8|9|\color{red}square|\color{blue}11|\color{blue}2|\color{blue}5|\color{red}12|13|6|14|1|7`.
Bei der Fehlerzählung sind demnach jeweils die drei blauen Werte betroffen:
Durch die Verschiebung drehen sich bei diesen Paaren die Reihenfolgen genau um.
Wenn es vor der Verschiebung bei einem dieser drei Werte einen Fehler gab, taucht er jetzt nicht mehr auf, wenn es keinen Fehler gab, gibt es jetzt an dieser Stelle einen Fehler.
Wenn es z.B. vorher `3` Fehler gab [ wie in diesem Beispiel `\color{blue}13 | \color{red}1`, `\color{blue}6 | \color{red}1`, `\color{blue}14 | \color{red}1` ], dann gibt es nach der Verschiebung `0` Fehler.
Wenn es vorher `2` Fehler gab, gibt es danach `1` Fehler, bei `1` Fehler werden es `2` und eine fehlerlose Dreierpaarbeziehung :-) wird zu `3` Fehlerpaaren.
Die neue Fehleranzahl `f` unterscheidet sich demnach von der alten Anzahl um `+-3` oder `+-1`.
Bei einer Verschiebung nach unten sind die Beziehungen genauso verteilt.
Neben dieser Änderung durch die Senkrechtverschiebung wird zusätzlich die Zeile des Leerfeldes um `1` verändert.
In diesem Beispiel von Zeile `3` auf Zeile `4` bzw. auf Zeile `2`.
Insgesamt gibt es bei der Senkrechtverschiebung also immer eine ungerade Anzahl der Änderung der Fehleranzahl:
`-3 | -1 | +1 | +3` und eine Änderung der Lückenzeile um `+1` oder `-1`.
Wenn man diese beiden Werte addiert, muss sich demnach immer eine gerade Zahl ergeben: `-4 | -2 | ... | +4`.
Nach einem beliebigen Mischen der Werte hat das Puzzle am Anfang eine Fehleranzahl von `f` und das Leerfeld steht in einer Reihe `r` zwischen `1` und `4`.
Die Summe aus diesen beiden Zahlen `f + r` ist damit festgelegt und ist entweder gerade oder ungerade.
Durch die Verschiebung eines Wertes ändert sich diese Summe bei einer waagerechten Verschiebung nicht und bei einer senkrechten Verschiebung um eine gerade Zahl.
Wenn die Summe `f + r` nach dem Mischen demnach eine gerade Zahl war (im Beispiel `53 + 3 = 56`), bleibt sie immer gerade, wenn sie ungerade war, bleibt sie immer ungerade.
Das gelöste Puzzle hat aber einen Summenwert von `0 + 4 = 4`
[Es ist kein Fehler vorhanden und das leere Feld ist in Zeile 4.].
Ein Puzzle, das am Anfang einen ungeraden Summenwert besitzt, kann demnach nie in das gelöste Puzzle überführt werden.
Das Puzzle mit einer geraden Summe kann aber in ein Puzzle mit dieser Summe `4` gebracht werden, es ist demnach lösbar.
Das Beispielpuzzle ist demnach lösbar!
Anhand dieses Summenwertes wird in der GeoGebra-App die Lösbarkeit entschieden.
P.S. Der Summenwert ist unter der grün/roten-Kennzeichnung der Lösbarkeit durch einen Mausklick als Zahl abrufbar.

