Druckversion vom 15.05.2024 07:55 Uhr
Startseite Vorkurs Weitere Gleichungen und Funktionen Quadratische Funktionen (Parabeln)
Quadratische Funktionen - Lehrtext
Für ein erfolgreiches Arbeiten mit quadratischen Funktionen sind die Kenntnis und der sichere Umgang der nachfolgenden Begriffe erforderlich. Falls Sie Ihre Kenntnisse auffrischen wollen, so werden Sie hier fündig.
Quadratische Funktion in Normalform: `f(x)=a*x^2+b*x+c`
Quadratische Funktion in Scheitelpunktform: `f(x)=a*(x-d)^2+e`
Umwandlung der beiden Formen ineinander
Nullstellen einer quadratischen Funktion: `f(x)=0`
Parabel als Graph einer quadratischen Funktion
Normalparabel : Graph von `f(x)=x^2`
Bedeutung des Faktors a vor x2 für Öffnungsrichtung, Stauchung und Streckung einer Parabel
Bedeutung der Parameter d und e für die Verschiebung einer Parabel
Es folgt nun eine Zusammenstellung von wichtigen Grundaufgaben.
Zur Beschreibung gehören die Nullstellen, der Schnittpunkt mit der y-Achse, der Scheitelpunkt, die Öffnung der Parabel.
|
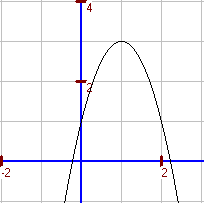
Beispiel 1 (Normalform gegeben): `f(x)=-2x^2+4x+1` Es gilt `a=-2; b= 4; c=1` Da `a < 0`, ist die Parabel nach unten geöffnet. Da `a < -1`, ist sie schmaler als eine Normalparabel bzw. gegenüber einer Normalparabel gestreckt. Nullstellen: `-2x^2+4x+1=0 hArr x^2-2x-0,5=0` `x_(1","2)=1+-sqrt(1+0,5)`, also `x_1~~2,2` und `x_2~~-0,22` Schnittpunkt mit der y-Achse: `f(0)=1`, also ist (0; 1) der Schnittpunkt mit der y-Achse. Scheitelpunkt: Da der x-Wert `x_s` des Scheitelpunktes in der Mitte der Nullstellen liegt, gilt `x_2=1` (`=-p/2` - siehe p-q-Formel) `f(1)=3`, also ist S(1; 3) der Scheitelpunkt. Scheitelpunktform: `f(x)=-2(x-1)^2+3` |
 |
|
Beispiel 2 (Scheitelpunktform gegeben): `f(x)=0,5(x+1)^2-2` `a=0,5; d=-1; e=-2` Da a > 0, ist die Parabel nach oben geöffnet. Da `a < 1`, ist die Parabel breiter als eine Normalparabel bzw. gegenüber einer Normalparabel gestaucht. Schnittpunkt mit der y-Achse: `f(0)=-1,5`, also ist (0; -1,5) der Schnittpunkt mit der y-Achse. Scheitelpunkt: S(-1; -2) Nullstellen: `0,5(x+1)^2-2=0 hArr 0,5(x+1)^2=2` `hArr (x+1)^2=4 hArr x+1=2 vv x+1=-2` `x_1=1` und `x_2=-3` Normalform: `0,5(x+1)^2-2=0,5(x^2+2x+1)-2` `=0,5x^2+x+0,5-2=0,5x^2+x-1,5` |
 |
- Ablesen der Koordinaten des Scheitelpunktes `S(x_s;y_s)` und Eintragen der beiden Werte in die Scheitelpunktform: `f(x)=a*(x-x_s)+y_s`.
- Vom Scheitelpunkt eine Einheit nach rechts gehen und ablesen, wie weit man von dort nach oben (ergibt a > 0) oder unten (ergibt a < 0) gehen muss, bis man wieder auf den Graphen trifft. Den Wert (mit Vorzeichen) für a in die Scheitelpunktform eintragen.
- Ist der Wert für a in der Grafik schlecht ablesbar, dann liest man irgendeinen gut ablesbaren Punkt auf dem Graphen ab (nicht S, da der Punkt oben schon ausgewertet wurde), setzt den x-Wert in die Scheitelpunktform für x ein und den y-Wert für f(x). Da `x_s` und `y_s` schon eingetragen sind, erhält man eine Gleichung, in der nur noch a unbekannt ist. Die Gleichung ist zu lösen.
- Soll die Normalform der Funktionsvorschrift bestimmt werden, so wird ausmultipliziert.
|
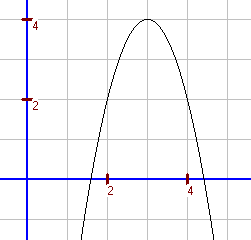
Beispiel 1: S(3; 4), also folgt: `f(x)=a*(x-3)^2+4` Geht man vom Scheitelpunkt 1 Kästchen nach rechts und 2 Kästchen nach unten, so trifft man auf einen weiteren Punkt des Graphen. Also gilt `a = -2`. Also: `f(x)=-2(x-3)^2+4` (Scheitelpunktform) `hArr f(x)=-2(x^2-6x+9)+4` `hArr f(x)=-2x^2+12x-14` (Normalenform) |
 |
|
Beispiel 2: S(-1; -2), also folgt: `f(x)=a*(x+1)^2-2` Ein weiterer Punkt des Graphen ist (1; 0): `f(1)=0 hArr a*(1+1)^2-2=0 hArr 4a-2=0 hArr a=0,5` Also: `f(x)=0,5(x+1)^2-2` `hArr f(x)=0,5(x^2+2x+1)-2` `hArr f(x)=0,5x^2+x-1,5` |
 |
- Sind `S(x_s;y_s)` und a gegeben, so setzt man die drei Daten in die Scheitelpunktform ein und ist fertig: `f(x)=a*(x-x_s)+y_s`. Falls gewünscht, erhält man die Normalform durch Ausmultiplizieren.
- Ist S und ein weiterer Punkt gegeben, so setzt man `x_s` und `y_s` in die Scheitelpunktform ein und geht vor wie oben unter 3.
- Sind drei Punkte gegeben, so wählt man die Normalform und setzt den x-Wert des ersten Punktes für x ein, den y-Wert für f(x). Macht man das für alle drei Punkte, so erhält man drei Gleichungen, die nur noch a, b und c als Variablen enthalten. Das Gleichungssystem muss dann gelöst werden. Ggf. ist die Normalform in die Scheitelpunktform umzuwandeln.
- Sind die Nullstellen `x_1, x_2` und a gegeben, so erhält man eine Funktionsgleichung wie folgt: `f(x)=a*(x-x_1)*(x-x_2)`.
- Sind die Nullstellen `x_1,x_2` und ein weiterer Punkt gegeben, so setzt man in `f(x)=a*(x-x_1)*(x-x_2)` die Koordinaten diese Punktes ein und berechnet a.
Beispiel 1:
S(0; 4), `a=-2`:
`f(x)=-2(x-0)^2+4 hArr f(x)=-2x^2+4`
Beispiel 2:
S(1; -2), P(3; 4):
`f(x)=a*(x-1)^2-2` und `f(3)=4`.
Es folgt: `a*(3-1)^2-2=4 hArr 4a-2=4 hArr a=1,5`.
Also: `f(x)=1,5(x-1)^2-2`
|
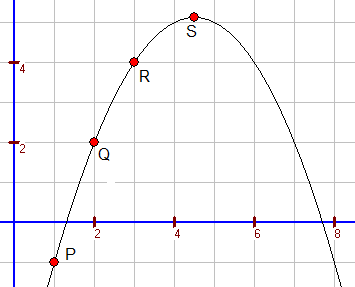
Beispiel 3: P(1; -1), Q(2; 2), R(3; 4) `f(x)=a*x^2+b*x+c` I: `f(1)=-1 hArr a+b+c=-1` II: `f(2)=2 hArr 4a+2b+c=2` III: `f(3)=4 hArr 9a+3b+c=4` IV: `3a+b=3` (II - I) V: `8a+2b=5` (III - I) VI: `2a=-1 hArr a=-0,5` (V - 2·IV) IV: `3·(-0,5)+b=3 hArr b=4,5` I: `-0,5+4,5+c=-1 hArr c=-5` Ergebnis: `f(x)=-0,5x^2+4,5x-5` Umwandlung in die Scheitelpunktform: Methode 1 (quadratische Ergänzung) `f(x)=-0,5x^2+4,5x-5 hArr -2*f(x)=x^2-9x+10` `hArr -2*f(x)+(9/2)^2=x^2-9x+(9/2)^2+10` `hArr -2*f(x)+(9/2)^2=(x-9/2)^2+10` `hArr -2*f(x)=(x-9/2)^2-10,25` `hArr f(x)=-0,5(x-4,5)^2+5,125` Methode 2 (mithilfe der p-q-Formel `x_s=-p/2`) `-0,5x^2+4,5x-5=0 hArr x^2-9x+10=0` `x_s=4,5` und `f(4,5)=5,125` S(4,5; 5,125) `f(x)=-0,5(x-4,5)^2+5,125` |
 |
Beispiel 4:
`x_1=-1,x_2=5, a=-2`
`f(x)=-2*(x+1)*(x-5)=-2(x^2-4x-5)=-2x^2+8x+10`
Beispiel 5:
`x_1=-1,x_2=5`; P(3; 1)
`f(x)=a*(x+1)*(x-5)`
`f(3)=1 hArr 1=a*4*(-2) hArr a=-1/8`
Also: `f(x)=-1/8*(x+1)*(x-5)=-1/8*(x^2-4x-5)=-1/8x^2+1/2x+5/8`
Zeichnen Sie den Scheitelpunkt in das Koordinatensystem.
|
1. Ist a = 1, dann liegt eine (verschobene) Normalparabel vor. Lesen Sie die Koordinaten von S ab und zeichnen Sie ihn ein. Gehen Sie von S eine Einheit nach rechts und eine nach oben, eine nach links und eine nach oben, zwei nach rechts und vier nach oben, zwei nach links und vier nach oben. Im Bild: `f(x)=(x-3)^2+1` |
|
|
2. Ist a = -1, so verfahren Sie ebenso, gehen nur jeweils eine bzw. vier Einheiten nach unten statt nach oben. Im Bild: `f(x)=-(x-3)^2+1` |
|
|
3. Ist a nicht 1 oder -1, so gehen Sie vom Scheitelpunkt S eine Einheit nach rechts und den Wert von a je nach Vorzeichen nach oben oder unten, ebenso eine Einheit nach links; zwei nach rechts und 4a nach oben bzw. unten, ebenso zwei nach links. Im Bild: `f(x)=1","5*(x-3)^2-1` |
Verbinden Sie die 5 Punkte elegant durch eine Kurve (keine Strecken zeichnen).
Dazu gibt es zwei verschiedene Wege:
Weg 1
Erstellen einer kompletten Wertetabelle, Punkte einzeichnen und elegant verbinden (umständlich, anfällig für Rechenfehler und in der Regel nicht zu empfehlen). Zudem wird der Scheitelpunkt evtl. nicht getroffen.
Weg 2
Bestimmen charakteristischer Punkte der Parabel, Einzeichnen und elegante Verbindung dieser Punkte zu einer Parabelkurve. Sinnvolle Punkte/Stellen sind:
- die Nullstellen: durch p-q-Formel oder quadratische Ergänzung bestimmen,
- der Scheitelpunkt: der x-Wert liegt mitten zwischen den beiden Nullstellen (falls vorhanden),
bzw. noch leichter: der x-Wert des Scheitelpunktes ergibt sich direkt als `x_s=-p/2` aus der p-q-Formel bei der Nullstellen-Bestimmung oben (auch wenn keine Nullstellen existieren).
Den Funktionswert `y_s` des Scheitelpunktes gewinnt man durch Einsetzen: `y_s=f(x_s)`. - der Schnittpunkt mit der y-Achse: Ablesen von c in der Funktionsvorschrift.
Die vier Punkte müssen dann noch elegant zu einer Kurve verbunden werden. Falls es keine Nullstellen gibt, hat man nur 2 Punkte. Dann sollte man zwei weitere Punkte (wie in einer Wertetabelle) zusätzlich bestimmen.
Beispiel zum Weg 2:
|
`f(x)=-2x^2-4x+1` Nullstellen: `-2x^2-4x+1=0 hArr x^2+2x-1/2=0` Es folgt: `x_(1","2)=-1+-sqrt(1+1/2)` `x_1~~0,22` und `x_2~~-2,22` P(-2,22; 0) und Q(0,22; 0) Scheitelpunkt S(-1; f(-1))= S(-1; 3) Schnittpunkt mit der y-Achse: R(0; 1) |
 |

