Druckversion vom 20.04.2024 13:44 Uhr
Startseite Vorkurs Weitere Gleichungen und Funktionen Prozentrechnung
Prozentrechnung/Wachstumsfaktor - Lehrtext
Das Zeichen % (gelesen: Prozent) wird in Verbindung mit einer davor stehenden Zahl benutzt und stellt einen Bruch mit dem Nenner 100 dar.
Beispiel: `5% = 5/100 = 0,05`
Auswendig sollte man wissen:
`1/2=50%`; `1/3~~33,3%`; `1/4=25%`; `1/5=20%`; `1/8=12,5%`; `1/10=10%`. Außerdem Vielfache davon wie z. B.: `3/4=75%`; `5/8=62,5%`; `3/2=150%`.
Steht hinter einer Prozentangabe das Wort "von" so bedeutet dies eine Multiplikation.
Beispiel: 7% von 60 bedeutet `7/100·60=4,2`.
7 ist die Prozentzahl (p) 7 % ist der Prozentsatz (`p%=p/100`), 60 ist der Grundwert (G) und 4,2 ist der Prozentwert (W).
Das Zeichen ‰ (gelesen: Promille) wird in Verbindung mit einer davor stehenden Zahl benutzt und stellt einen Bruch mit dem Nenner 1000 dar.
Beispiel: `5‰ = 5/1000 = 0,005 = 0,5%`
Die nebenstehende Graphik zeigt den Zusammenhang: 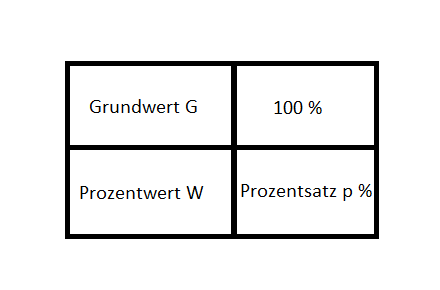
1. Bestimmung des Prozentwertes: `W=G*p/100`
Beispiel:
Ein Schrank kostet 800 €. 25 % davon sind Materialkosten. Wie teuer ist das Material? Oder: Wie viel ist 25 % von 800 €?
`W=800*25/100=200`
Die Materialkosten betragen 200 €.
2. Bestimmung des Grundwertes: `G=(100*W)/p` (erhält man durch Umformung aus der Formel bei 1.)
Beispiel:
Eine 2,5 % Lohnerhöhung ergibt 80 €. Wie hoch war der Lohn vor der Lohnerhöhung?
`G=(100*80)/(2","5)=3200`
Vor der Erhöhung betrug der Lohn 3200 €.
3. Bestimmung des Prozentsatzes: `p/100=W/G` (erhält man durch Umformung aus der Formel bei 1.)
Beispiel:
2 kg Messing enthalten 1,5 kg Kupfer und 0,5 kg Zink. Wie viel Prozent beträgt der Kupferanteil?
`p/100=(1","5)/2=0","75=75/100`
Der Kupferanteil beträgt 75 %.
Beispiel 1:
Der Netttopreis für einen Kühlschank beträgt 530 €. Der Verkaufspreis (Bruttopreis) ergibt sich durch einen Aufschlag von 19% (Mehrwertsteuer), d.h. der Verkaufspreis beträgt 119% des Nettopreises (100% + 19% Aufschlag). Der Nettopreis ist somit der Grundwert G und der Prozentsatz p% beträgt 119%. Der Verkaufspreis ist der Prozentwert W.
`W=530*119/100=530*1","19=630","70`.
Der Verkaufspreis beträgt 630,70 €.
Der Faktor 1,19 heißt auch Zunahmefaktor a.
Es gilt: a = 1 + p%, wenn p% die Zunahme ist.
Beispiel 2:
Ein Artikel kostet 249 €. Der Verkäufer gewährt einen Rabatt von 5%. Der Kunde zahlt also nur 95 % (100 % - 5 %) des ursprünglichen Preises.
`W=249*95/100=249*0","95=236,"55`.
Der Kunde zahl 236,55 €.
Der Faktor 0,95 heißt auch Abnahmefaktor a.
Es gilt: a = 1 - p%, wenn p% die Abnahme ist.
Hinweis 1:
Gelegentlich wird eine Abnahme auch mit einem negativen p angegeben. Dann gilt a = 1 + p%.
Beispiel:
Eine Veränderung um -5 % ergibt a = 1 + (-5 %) = 0,95
Hinweis 2:
Der Faktor a heißt auch Wachstumsfaktor:
| a = 0 | 0 < a < 1 | a = 1 | a > 1 |
|---|---|---|---|
| Abnahme um 100 % | Abnahme | Keine Veränderung (p = 0 %) | Zunahme |
Beispiel für die Bestimmung von W:
Siehe die vorstehenden beiden Beispielen.
Beispiel für die Bestimmung von G:
Ein Monatslohn ist nach einer Erhöhung um 4,2% auf 2344,50 € gestiegen. Wie hoch war der Lohn vorher?
`G*1,042= 2344,50 hArr G=2250`.
Der Lohn betrug vorher 2250 €.
Beispiel für die Bestimmung von p:
Ein Händler gibt eine Ware, deren Verkaufspreis mit 254 € angegeben ist für 241,30 € ab. Wie hoch ist der Rabatt?
`(241","30)/254=0","95`. Der Abnahmefaktor beträgt 0,95, d.h. die prozentuale Abnahme ist 1 - 0,95 = 0,05 = 5 %.
Ein Geldbetrag wird für 3 Jahre fest angelegt und im 1. Jahr mit 4 %, im 2. Jahr mit 5 % und im 3. Jahr mit 5,5 % verzinst.
1. Wie hoch ist der Auszahlungsbetrag (Endkapital) am Ende des dritten Jahres, wenn der Anlagebetrag (Anfangskapital) 5000 € beträgt? Wie hoch ist die Gesamtverzinsung?
Lösung: `5000*1","04*1","05*1","055=5000*1","15206=5760","30`
Das Endkapital beträgt 5760,30 €. Die Gesamtverzinsung beträgt 1,15206 - 1 = 15,206 %.
2. Wie viel Geld (K) muss man anlegen, wenn man 10.000 € ansparen will?
Lösung: `K*1","04*1","05*1","055=10000 hArr K*1","15206=10000 hArr K~~8680,10`
Man muss 8680,10 € anlegen.
3. Wie hoch ist die durchschnittliche Verzinsung?
Ansatz 1
`a= (4 %+5 %+5,5 %)/3~~4,833 %`
Probe: `1","04833^3!=1","04*1","05*1","055`, also ist der Ansatz falsch.
Ansatz 2
`a=(1","04+1","05+1","055)/3~~1","04833` (siehe Ansatz 1)
Korrekte Lösung:
Es muss gelten `a*a*a=1","04*1","05*1","055 hArr a=root(3)(1","04*1","05*1","055)~~1"","04831`
Der durchschnittliche Zunahmefaktor beträgt ca. 1,04831 bzw. die durchschnittliche Verzinsung beträgt ca. 4,831 %.
Verallgemeinerung:
Hat man in n aufeinander folgenden Perioden die Zunahme- bzw. Abnahmefaktoren `a_1` bis `a_n`, dann gilt
- `a_1*a_2*...*a_n` ist der Gesamtzunahme-/Gesamtabnahmefaktor.
- Ist `a_1*a_2*...*a_n > 1`, dann ist die gesamte prozentuale Zunahme `a_1*a_2*...*a_n-1` .
Ist `a_1*a_2*...*a_n = 1`, dann gibt es insgesamt keine Veränderung.
Ist `a_1*a_2*...*a_n < 1`, dann ist die gesamte prozentuale Abnahme `1-a_1*a_2*...*a_n` - `a=root(n)(a_1*a_2*...a_n)` ist der durchschnittliche Zunahme-/Abnahmefaktor.
`root(n)(a_1*a_2*...a_n)` heißt auch geometrisches Mittel der Zahlen `a_1` bis `a_n`.

