Druckversion vom 19.04.2024 22:33 Uhr
Startseite Vorkurs Weitere Gleichungen und Funktionen Funktionsbegriff
Funktionsbegriff - Aufgaben
 Aufgabe 1 Aufgabe 1 |
|
Gegeben sind die Funktionen f(x) = -x2 + x und g(x) = 2x2 + 1. Tragen Sie Ihr Ergebnis in die freien Felder ein.
a. Berechnen Sie den Funktionswert von f an der Stelle 4. b. Welchen Wert nimmt der Funktionsterm von g für -3 an? c. Welchen y-Wert hat der Punkt auf dem Grafen von g an der Stelle 5? d. Berechnen Sie f(x) für x = 6. e. Bestimmen Sie g(1,25). f. Bestimmen Sie zu f die Punktkoordinaten P(-1/ ). |
 Aufgabe 2 Aufgabe 2 |
|
Gegeben ist f(x)=-2x2 - x.
Ziehen Sie die unten stehenden Ergebnisse in die freien Felder.
a. Berechnen Sie den Funktionswert von f an der Stelle m. b. Welchen Wert nimmt der Funktionsterm von f für -x an? c. Welchen y-Wert hat der Punkt auf dem Grafen von f an der Stelle a + h? d. Berechnen Sie f(x) für x = a - h. e. Bestimmen Sie f(a2). f. Bestimmen Sie zu f die Punktkoordinaten P(-a/ ). -2m2 - m -2x2 + x -2a2 -4ah - 2h2 - a - h -2a2 + 4ah - 2h2 -a + h -2a4 - a2 -2a2 + a |
 Aufgabe 3 Aufgabe 3 |
|
Tragen Sie Ihr Ergebnis in die freien Felder ein.
a. Berechnen Sie den passenden x-Wert. Gegeben ist y = 1 und f(x) = x7. b. Bestimmen Sie zu g(x) = -3x +7 die fehlende Koordinate des Graphenpunktes P( ; 19). c. Welchen x-Wert hat der Punkt P( ; 15) auf dem Grafen von f(x) = 2x3 - 1? d. Gegeben ist f(x) = 2x + 4. Berechnen Sie x für f(x) = 5. e. Für welchen x-Wert nimmt die Funktion g(x) = -x3 - 1 den Wert 0 an? |
 Aufgabe 4 Aufgabe 4 |
|
Ziehen Sie die unten stehenden Ergebnisse in die freien Felder.
a. Berechnen Sie passende x-Werte. y = 1 und f(x) = x4. b. Für welche x-Werte nimmt die Funktion g(x) = 4x2 den Wert 36 an? c. Berechnen Sie zu f(x) = x4 die fehlende Punktkoordinate P( ; 16). d. Gegeben ist f(x) = -2x2 +2. Berechnen Sie x für f(x) = -48. e. Für welchen x-Wert nimmt die Funktion g(x) = x4 +1 den Wert 1 an?. x1 = 1 und x2 = -1 x1 = 3 und x2 = -3 x1 = 2 und x2 = -2 x1 = 5 und x2 = -5 0 |
 Aufgabe 5 Aufgabe 5 |
|
Erstellen Sie eine Wertetabelle für x-Werte von -2 bis 2. Tragen Sie die Punkte der Wertetabelle jeweils in ein Koordinatensystem ein und verbinden Sie diese elegant zu einem Graphen.
|
 Aufgabe 6 Aufgabe 6 |
||||||||||||||||||||||||||||||||||||||
|
Markieren Sie die richtigen Aussagen
|
 Aufgabe 7 Aufgabe 7 |
|
|
Ein Autofahrer fährt von zu Hause zur Arbeit. Welcher der Grafen A bis D oben passt zu welcher Geschichte?
|
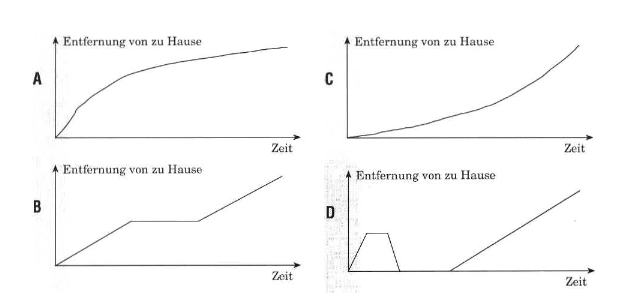 |
 Aufgabe 8 (siehe Lehrtext) Aufgabe 8 (siehe Lehrtext) |
|
|
Ein Schüler gelangt von seiner Wohnung über eine geradlinige Straße zu seiner Schule. Betrachtet wird die Funktion "Dauer des Weges → Entfernung von der Wohnung". In nebenstehender Zeichnung sind auf der x-Achse die Minuten seit dem Verlassen der Wohnung und auf der y-Achse die Entfernung von der Wohnung in Metern abgetragen. Beschreibung des Schulweges: Bestimmen Sie die Gleichung der einzelnen Geradenstücke.
|
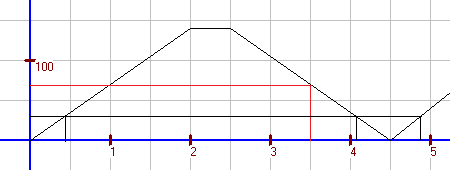 |


 Falls Sie keine Idee haben
Falls Sie keine Idee haben